2022年苏科版初中数学《中考一轮复习》专题四 图形的认识 4.6 正方形
试卷更新日期：2022-01-18 类型：一轮复习
一、单选题
-
1. 四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”（如图），其直角三角形的两条直角边长分别为2和3，则小正方形与大正方形的面积比是（ ）
A、1：13 B、1：14 C、2：9 D、2：152. 如图，在平面直角坐标系中，四边形ABCO是正方形，已知点C的坐标为（ ，1），则点B的坐标为（ ）
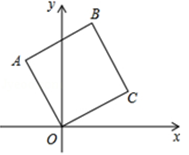A、 B、 C、 D、3. 如图，E是正方形ABCD的边DC上一点，过点A作FA＝AE交CB的延长线于点F，若AB＝4，则四边形AFCE的面积是（ ）
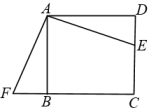A、4 B、8 C、16 D、无法计算4. 如图，正方形ABCD的边长为3，将正方形ABCD沿直线EF翻折，则图中折成的4个阴影三角形的周长之和是（ ）
A、8 B、9 C、12 D、以上都不正确5. 如图，在边长为2的正方形 中，若将 绕点 逆时针旋转 ，使点 落在点 的位置，连接 ，过点 作 ，交 的延长线于点 ，则 的长为（ ）
A、 B、 C、 D、6. 如图，正方形ABCD中，点E，F分别在BC，CD上， 是等边三角形，连接AC交EF于G，下列结论：① ，② ，③AC垂直平分EF，④ ．其中错误结论的是（ ）
A、① B、② C、③ D、④7. 如图，正方形 和正方形 中，点D在 上， ， ，H是 的中点，那么 的长是（ ）
A、3 B、 C、 D、8. 如图，在正方形ABCD中， ，E，F分别为边AB，BC的中点，连接AF，DE，点N，M分别为AF，DE的中点，连接MN，则MN的长为（ ）
A、 B、1 C、 D、29. 如图，正方形ABCD的面积为25， ABE 为等边三角形，点E在正方形ABCD内，若P是对角线AC上的一动点，则PD+PE的最小值是（ ）
A、 B、5 C、 D、10. 如图，已知在正方形ABCD中，对角线AC与BD相交于点O，AE，DF分别是∠OAD与∠ODC的角平分线，AE的延长线与DF相交于点G，则下列结论：①AG⊥DF；②EF AB；③AB＝AF；④AB＝2EF.其中正确的有（ ）个.
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图，正方形ABCD的边长为4厘米，则图中阴影部分的面积为.
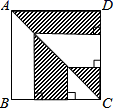12. 如图，直线a过正方形ABCD的顶点A ， 点B、D到直线a的距离分别为5、12，则正方形的周长为 ．
13. 如图，点E，F在正方形ABCD的对角线AC上，AC＝10，AE＝CF＝3，则四边形BFDE的面积为 ．
14. 如图，G、H分别是四边形ABCD的边AD、AB上的点，∠GCH=45°，CD=CB=2，∠D=∠DCB=∠B=90°，则△AGH的周长为.
15. 如图所示，在正方形ABCD中，点P在AC上， ， ，垂足分别为E，F， ，则DP的长为 ．
16. 如图，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG，EF交AD于点H，那么DH的长是 ．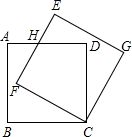
17. 如图，AD是锐角△ABC的BC边上的高，正方形EFGH的一边EF在BC上，顶点G，H分别在AC，AB上，若BC＝15，AD＝10，则EF的长为 .
18. 如图，在正方形ABCD中，AB=8，点M在CD边上，且DM=2，△AEM与△ADM关于AM所在直线对称，将△ADM按顺时针方向绕点A旋转90°得到△ABF，连接EF，则线段EF的长为 ．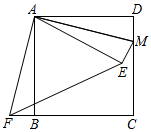
三、综合题
-
19. 如图，正方形ABCD与正方形A1B1C1D1关于某点中心对称，已知A，A1 ， B1三点的坐标分别是(0，5)，(0，1)，(3，1)．
(1)、求对称中心的坐标．(2)、写出顶点D，B，D1 ， C1的坐标．20. 如图，在正方形ABCD中，点P在对角线BD上，PE⊥BC，PF⊥CD，垂足分别为E、F．求证：AP=EF．
21. 如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE=1，求EF的长.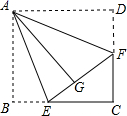
22. 已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．
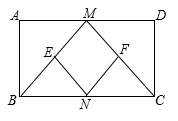(1)、求证： ；(2)、判断四边形MENF是什么特殊四边形，并证明你的结论；(3)、当AD，AB满足什么条件时，四边形MENF是正方形．23. 如图1，在正方形ABCD的外侧，作两个等边三角形ADE和DCF，连接AF，BE．
(1)、请判断：AF与BE的数量关系是 ， 位置关系是；(2)、如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC，第（1）问中的结论是否仍然成立？请作出判断并给予说明；(3)、若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断．24. 如图：
(1)、如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF；(2)、如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用（1）的结论证明：GE=BE+GD．(3)、运用（1）（2）解答中所积累的经验和知识，完成下题：如图3，在四边形ABCG中，AG∥BC（BC＞AG），∠B=90°，AB=BC，E是AB上一点，且∠GCE=45°，BE=4，AG=6，求四边形ABCG的面积．25. 如图1，在矩形 中，点 分别在 边上， 于点 ．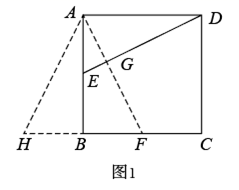
(1)、求证：四边形 是正方形；(2)、延长 到点 ，使得 ，判断 的形状，并说明理由．(3)、如图2，在菱形 中，点 分别在 边上， 与 相交于点 ， ，求 的长．
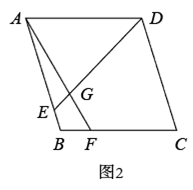26. 如图①，在正方形 中， ， 为对角线 上任意一点（不与 重合），连接 ，过点 作 ，交线段 于点 .
(1)、求证： ；(2)、若 ，求证： ；(3)、如图②，连接 交 于点 ．若 ，求 的值．
27. 如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC ， GF⊥CD ．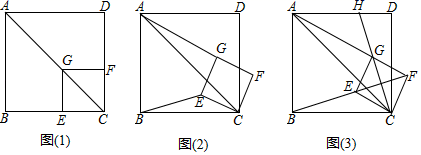
(1)、①求证：四边形CEGF是正方形；②推断： 的值为 ▲ ：
(2)、将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系；(3)、正方形CEGF在旋转过程中，当B ， E ， F三点在一条直线上时，如图（3）所示，延长CG交AD于点H ． 若AG＝6，GH＝2 ，求正方形CEGF和正方形ABCD的边长．28. （模型引入）我们在全等学习中所总结的“一线三等角、K型全等”这一基本图形，可以使得我们在观察新问题的时候很迅速地联想，从而借助已有经验，迅速解决问题．
（模型探究）
如图，正方形ABCD中，E是对角线BD上一点，连接AE ， 过点E作EF⊥AE ， 交直线CB于点F ．
(1)、如图1，若点F在线段BC上，写出EA与EF的数量关系并加以证明；(2)、如图2，若点F在线段CB的延长线上，请直接写出线段BC ， BE和BF的数量关系．(3)、（模型应用）
如图3，正方形ABCD中，AB＝4，E为CD上一动点，连接AE交BD于F ， 过F作FH⊥AE于F ， 过H作HG⊥BD于G ． 则下列结论：①AF＝FH；②∠HAE＝45°；③BD＝2FG；④△CEH的周长为8．正确的结论有个．(4)、如图4，点E是正方形ABCD对角线BD上一点，连接AE ， 过点E作EF⊥AE ， 交线段BC于点F ， 交线段AC于点M ， 连接AF交线段BD于点H ． 给出下列四个结论，①AE＝EF；② DE＝CF；③S△AEM＝S△MCF；④BE＝DE+ BF；正确的结论有 个．(5)、（模型变式）
如图5，在平面直角坐标系中，四边形OBCD是正方形，且D（0，2），点E是线段OB延长线上一点，M是线段OB上一动点（不包括点O、B），作MN⊥DM ， 垂足为M ， 交∠CBE的平分线与点N ， 求证：MD＝MN(6)、如图6，在上一问的条件下，连接DN交BC于点F ， 连接FM ， 则∠FMN和∠NMB之间有怎样的数量关系？请给出证明．(7)、（拓展延伸）
已知∠MON＝90°，点A是射线ON上的一个定点，点B是射线OM上的一个动点，且满足OB＞OA ． 点C在线段OA的延长线上，且AC＝OB ． 如图7，在线段BO上截取BE ， 使BE＝OA ， 连接CE ． 若∠OBA+∠OCE＝β ， 当点B在射线OM上运动时，β的大小是否会发生变化？如果不变，请求出这个定值；如果变化，请说明理由．(8)、如图8，正方形ABCD中，AD＝6，点E是对角线AC上一点，连接DE ， 过点E作EF⊥ED ， 交AB于点F ， 连接DF ， 交AC于点G ， 将△EFG沿EF翻折，得到△EFM ， 连接DM ， 交EF于点N ， 若点F是AB边的中点，则△EDM的面积是 ．