2022年苏科版初中数学《中考一轮复习》专题四 图形的认识 4.5 矩形与菱形
试卷更新日期：2022-01-18 类型：一轮复习
一、单选题
-
1. 矩形具有而菱形不一定具有的性质是（ ）A、两组对边分别平行且相等 B、邻角互补 C、对角线相等 D、对角线互相垂直2. 已知一个菱形的周长是20，两条对角线的比是4∶3，则这个菱形的面积是（ ）A、12 B、36 C、24 D、483. 如图，矩形ABCD中，AB＝6，如果将该矩形沿对角线BD折叠，那么图中阴影部分 BED的面积22.5，则BC=（ ）
A、16 B、10 C、12 D、144. 如图，在平面直角坐标系中，菱形OABC的顶点B在y轴正半轴上，顶点C在函数y=（x＜0）的图象上．若对角线AC=6，OB=8，则k的值是（ ）
A、24 B、12 C、﹣12 D、﹣65. 如图，在菱形ABCD中， ， ， 为等边三角形点E，F分别在菱形的边BC，CD上滑动，且E，F不与B，C，D重合，则四边形AECF的面积是（ ）
A、4 B、 C、8 D、6. 如图，已知菱形ABCD的两条对角线分别为6和8，M、N分别是边BC、CD的中点，P是对角线BD上一点，则PM+PN的最小值是（ ）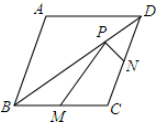
A、5 B、10 C、6 D、87. 如图，将矩形ABCD放置在平面直角坐标系的第一象限内，使顶点A，B分别在x轴、y轴上滑动，矩形的形状保持不变，若AB＝2，BC＝1，则顶点C到坐标原点O的最大距离为（ ）
A、1+ B、1+ C、3 D、8. 如图，矩形ABCD中，AB＝12，BC＝18.将矩形沿EF折叠，使点A落在CD边中点M处，点B落在N处.连接EM，以矩形对称中心O为圆心的圆与EM相切于点P，则圆的半径为（ ）
A、2.7 B、5.4 C、4.5 D、3.69. 如图，矩形ABCD和矩形CEFG，AB＝1，BC＝CG＝2，CE＝4，点P在边GF上，点Q在边CE上，且PF＝CQ，连结AC和PQ，N，M分别是AC，PQ的中点，则MN的长为（ ）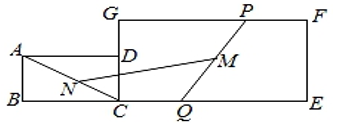
A、3 B、6 C、 D、10. 函数y＝ 和y＝ 在第一象限内的图象如图，点P是y＝ 的图象上一动点，PC⊥x轴于点C，交y＝ 的图象于点B．给出如下结论：①△ODB与△OCA的面积相等；②PA与PB始终相等；③四边形PAOB的面积大小不会发生变化；④CA＝ AP．其中所有正确结论的序号是（ ）
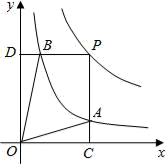A、①②③ B、②③④ C、①③④ D、①②④二、填空题
-
11. 如图，已知点A的坐标是 ， ， 点B的坐标是 ， ， 菱形的对角线交于坐标原点O，则点D的坐标是 ．
12. 在菱形ABCD中，AB＝5，BD＝8，P为对角线BD上的一个动点，过点P分别作AD、AB边的垂线，垂足分别为E、F两点，连接PE，PF，则PE+PF＝ ．
13. 如图，在菱形 中， ， 为垂足，若 ， ， 是 边上的一个动点，则线段 的长度的最小值是 ．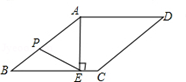
14. 如图，矩形ABCD 的对角线AC、BD 交于点O ， ∠AOD=60°，AB=2 ，AE⊥BD 于点E ， 则OE长 ．
15. 如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于点E，F，连接PB，PD.若AE＝2，PF＝8.则图中阴影部分的面积为.
16. 如图，在四边形 中，对角线 ，垂足为O，点E、F、G、H分别为边 、 、 、 的中点.若 ， ，则四边形 的面积为.
17. 如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为.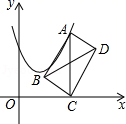
18. 如图，矩形 的顶点 在反比例函数 的图象上，且点 在第一象限，顶点 在 轴上，对角线 的延长线交 轴于点 ，若 的面积是 ，则 .
三、综合题
-
19. 如图，在菱形ABCD中，点E，F分别是边AB和BC上的点，且BE＝BF．求证：∠DEF＝∠DFE．
20. 如图，△ABC中，点D是边AC的中点，过D作直线PQ∥BC，∠BCA的平分线交直线PQ于点E，点G是△ABC的边BC延长线上的点，∠ACG的平分线交直线PQ于点F．求证：四边形AECF是矩形．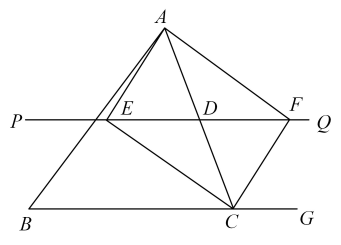
21. 已知：平行四边形ABCD的两边AB、BC的长是关于x的方程 的两个实数根．(1)、试说明：无论m取何值方程总有两个实数根(2)、当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；(3)、若AB的长为3，那么平行四边形ABCD的周长是多少？22. 如图，菱形ABCD的对角线AC、BD相交于点O ， 过点B作BE∥AC ， 且BE＝ AC ， 连接EC ．
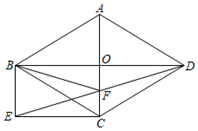(1)、求证：四边形BECO是矩形；(2)、连接ED交AC于点F ， 连接BF ， 若AC＝12，AB＝10，求BF的长．23. 如图，在矩形 中，对角线 与 相交于点 ， ，对角线 所在的直线绕点 顺时针旋转角 ，所得的直线 分别交 ， 于点 ， ．
(1)、求证： ；(2)、当旋转角 为多少度时，四边形 为菱形？试说明理由．24. 如图，在△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC交DE的延长线于F点，连接AD、CF，过D作DG⊥CF于点G．
(1)、求证：四边形ADCF是平行四边形；(2)、当△ABC满足什么条件时，四边形ADCF是菱形？为什么？(3)、在（2）的条件下，若AB＝6，BC＝10，求DG的长．25. 在平面直角坐标系中，已知O为坐标原点，点 ，以点A为旋转中心，把顺时针旋转，得.
（Ⅰ）如图①，当旋转后满足 轴时，求点C的坐标.
（Ⅱ）如图②，当旋转后点C恰好落在x轴正半轴上时，求点D的坐标.
（Ⅲ）在（Ⅱ）的条件下，边 上的一点P旋转后的对应点为 ，当 取得最小值时，求点P的坐标（直接写出结果即可）
26. 如图，在矩形 中， cm， cm.点 、 、 分别从点 、 、 三点同时出发，沿矩形的边按逆时针方向移动.点 、 的速度均为2cm/s，点F的速度为4cm/s，当点 追上点 （即点 与点 重合）时，三个点随之停止移动.设移动开始后第 秒时， 的面积为 （cm2）.
(1)、当 秒时， 的值是多少？(2)、当 等于多少秒时， 的值是18cm2；(3)、若点 在矩形的边 上移动，当 为何值时，以点 、 、 为顶点的三角形与以点 、 、 为顶点的三角形相似？请说明理由.27. （问题发现）数学小组成员小明做作业时遇到以下问题：
图1 图2 图3
(1)、若四边形 是菱形， ，点 是射线 上一动点，以 为边向右侧作等边 ，如图1，当点E在菱形 内部或边上时，连接 ，则 与 有怎样的数量关系？请直接写出你的猜想；(2)、（类比探究）数学小组对该问题进行进一步探究：若四边形 是正方形，点P是射线 上一动点，以 为直角边在 边的右侧作等腰 ，其中 .
①如图2，当点 在对角线 上时，小组发现点 恰好在射线 上，求 与 之间的数量关系（过程只用说明点 在线段 上的情况即可）；
②如图3，当P是对角线 的延长线上一动点时，小组发现点 恰好在射线 上，连接 ，若 ，求 的面积．
28. 小王在学习浙教版九上课本第72页例2后，进一步开展探究活动：将一个矩形ABCD绕点A顺时针旋转α（0°＜α≤90°），得到矩形AB′C′D′，连结BD ．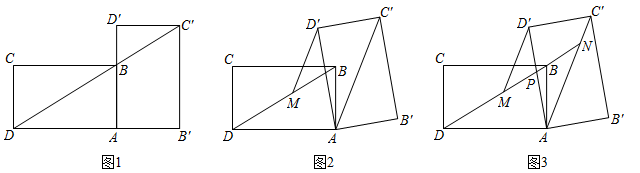
[探究1]如图1，当α＝90°时，点C′恰好在DB延长线上．若AB＝1，求BC的长．
[探究2]如图2，连结AC′，过点D′作D′M∥AC′交BD于点M ． 线段D′M与DM相等吗？请说明理由．
[探究3]在探究2的条件下，射线DB分别交AD′，AC′于点P ， N（如图3），发现线段DN ， MN ， PN存在一定的数量关系，请写出这个关系式，并加以证明．