2022年苏科版初中数学《中考一轮复习》专题四 图形的认识 4.4 多边形和平行四边形
试卷更新日期：2022-01-18 类型：一轮复习
一、单选题
-
1. 下列命题是真命题的是（ ）A、对角线互相垂直平分的四边形是正方形 B、对角线相等的四边形是平行四边形 C、对角线互相垂直的四边形是菱形 D、对角线互相平分且相等的四边形是矩形2. 一个多边形截去一个角后，形成新多边形的内角和为2 520°，则原多边形的边数为（ ）A、15 B、16 C、13或15 D、15或16或173. 如图，在平行四边形中，点在边上， ，连接交于点 ， 则的面积与的面积之比为（ ）
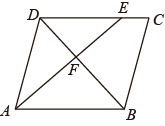A、 B、 C、 D、4. 如图，在平行四边形 中， 是 延长线上一点， 与 、 分别交于点 、 ．则下列说法错误的是（ ）
A、 B、 C、 D、5. 如图，D、E、F分别是 各边中点，则以下说法错误的是（ ）
A、 和 的面积相等 B、四边形 是平行四边形 C、若 ，则四边形 是菱形 D、若 ，则四边形 是矩形6. 如图，平行四边形 的对角线交于点 ，且 ，过点 作 ，交 于点 ．如果 的周长为7.5，那么平行四边形 的周长是（ ）
A、7.5 B、15 C、17 D、197. 如图，正方形 的边长为12， ， 分别为 ， 边上的点，且 ， ， 分别为 ， 边上的点，且 交 ， 于点 ， ，则 的长为（ ）
A、6 B、 C、 D、8. 如图，已知▱OABC的顶点A，C分别在直线 和 上，O是坐标原点，则对角线OB长的最小值为（ ）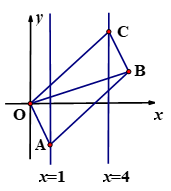
A、3 B、4 C、5 D、69. 如图，在▱ABCD中，∠A＝60°，AD＝2．以点A为圆心，AD为半径作 ，交边AB于点E，G是 的中点，作GF∥BC交CD于点F，以点F为旋转中心，将线段FG按逆时针方向旋转90°至线段FG′，若点G′恰好落在边BC上，则AB的长为（ ）
A、 B、 C、 D、10. 在▱ABCD中，∠DBC＝45°，DE⊥BC于E，BF⊥CD于F，BF交DE于点H，交AD的延长线于点G，下面结论中：①BD＝ BE；②∠A＝∠BHE；③CD2+BG2＝AG2；④BH×DG＝ED×GH.正确的结论是（ ）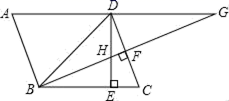
A、①②③ B、②③④ C、①②④ D、①②③④二、填空题
-
11. 如果一个多边形的内角和是 ，那么这个多边形的边数是.12. 如图，在 中， ， 平分 ，则 的度数是.
13. 如图，∠A+∠B+∠C+∠D+∠E+∠F＝ ．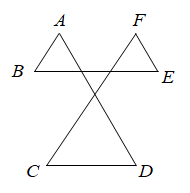
14. 如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高.若AB+AC＝8，S△ABC＝24，∠EDF＝120°，则AD的长为 .
15. 如图，AC是平行四边形ABCD的对角线，且AC⊥AB，在AD上截取AH＝AB，连接BH交AC于点F，过点C作CE平分∠ACB交BH于点G，且GF＝2 ，CG＝6，则AC＝.
16. 如图，在平行四边形ABCD中，E、F分别是AD、BC边上的点，AF与BE相交于点G ， DF与EC相交于点H ， 若S△ABG＝16，S△DHC＝7，则四边形EGFH的面积为 ．
17. 如图，在 中， 与 交于点 ，点 在 上， cm， cm， ，点 是 的中点，若点 以1cm/s的速度从点 出发，沿 向点 运动；点 同时以2cm/s的速度从点 出发，沿 向点 运动，点 运动到 点时停止运动，点 也同时停止运动，当点 运动时，以 、 、 、 为顶点的四边形是平行四边形．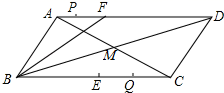
18. 如图，一副三角板如图1放置，AB＝CD，顶点E重合，将△DEC绕其顶点E旋转，如图2，在旋转过程中，当∠AED＝75°，连结AD，BC，AC，下列四个结论中说法正确的有 .①四边形ABCD是平行四边形；②CE垂直平分AB；③若AB2＝6，则BC2＝5+2 ；④DE⊥AC.
三、综合题
-
19. 一个多边形除一内角外，其余内角和与外角和之和为1560°.(1)、求该多边形的边数；(2)、若该多边形为正多边形，求每一个外角的度数.20. 如图，在平行四边形ABCD中，对角线AC、BD交于点O.M为AD中点，连接CM交BD于点N.
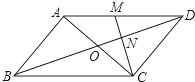(1)、求DN：BN的值：(2)、若ΔOCN的面积为2，求四边形AONM的面积.21. 如图，在平行四边形ABCD中，过点A分别作AE⊥BC于点E，AF⊥CD于点F．
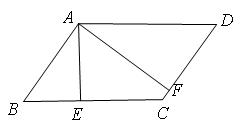(1)、求证：∠BAE=∠DAF；(2)、已知AE=4，AF=6，tan∠BAE= ， 求CF的长．22. 如图．在▱ABCD中，点E在边BC上，点F在边AD的延长线上，且DF=BE．EF与CD交于点G．
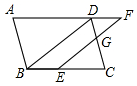(1)、求证：BD∥EF ．(2)、若 ，BE=4，求EC的长．23. 定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等.
理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD.
应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O.
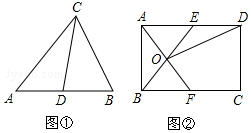(1)、求证：△AOB和△AOE是“友好三角形”；(2)、连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积.24. 如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连结AE，F为AE上一点，且∠BFE=∠C
(1)、求证：△ABF∽△EAD(2)、若AB=4，S ABCD= ，求AE的长(3)、在（1）、（2）条件下，若AD=3，求BF的长（计算结果可含根号）25. 综合与实践问题情境：数学活动课上，老师出示了一个问题：如图①，在平行四边形ABCD中，BE⊥AD，垂足为E，F为CD的中点，连接EF，BF，试猜想EF与BF的数量关系，并加以证明.
(1)、独立思考：请解答老师提出的问题；
(2)、实践探究：希望小组受此问题的启发，将平行四边形ABCD沿着BF（F为CD的中点）所在直线折叠，如图②，点C的对应点为C′，连接DC′并延长交AB于点G，请判断AG与BG的数量关系，并加以证明.
(3)、问题解决：智慧小组突发奇想，将▱ABCD沿过点B的直线折叠，如图③，点A的对应点为A′，使A′B⊥CD于点H，折痕交AD于点M，连接A′M，交CD于点N.该小组提出一个问题：若此平行四边形ABCD的面积为20，边长AB＝5，BC＝2 ，求图中阴影部分（四边形BHNM）的面积.请你思考此问题，直接写出结果.
26. 定义：有一组对边平行，有一个内角是它对角的一半的凸四边形叫做半对角四边形，如图1，直线 ，点A，D在直线 上，点B，C在直 上，若∠BAD＝2∠BCD，则四边形ABCD是半对角四边形.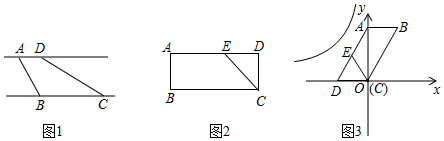
(1)、如图2，点E是矩形ABCD的边AD上一点，AB＝1，AE＝2.若四边形ABCE为半对角四边形，求AD的长：(2)、如图3，以▱ABCD的顶点C为坐标原点，边CD所在直线为x轴，对角线AC所在直线为y轴，建立平面直角坐标系.点E是边AD上一点，满足BC＝AE＋CE.求证：四边形ABCE是半对角四边形；(3)、在（2）的条件下，当AB＝AE＝ ，∠B＝60°时，将四边形ABCE向左平移a（a＞0）个单位后，恰有两个顶点落在反比例函数 的图象上，求k的值.