2022年苏科版初中数学《中考一轮复习》 专题四 图形的认识 4.2 三角形
试卷更新日期：2022-01-18 类型：一轮复习
一、单选题
-
1. 下列长度的三条线段首尾顺次相接，能够组成三角形的是（ ）A、3，5，10 B、5，7，12 C、4，4，8 D、8，8，102. 已知三角形三个内角的度数之比为3：3：4，则这个三角形是（ ）A、等腰三角形 B、直角三角形 C、钝角三角形 D、等边三角形3. 若一个三角形的三边长为a，b，c，且满足a2-2ab+b2+ac-bc =0，则这个三角形是（ ）A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形4. 在计算一个多边形的内角和时，由于粗心少算了1个内角，其和等于1180°，则少算的这个角的度数是（ ）A、60 B、70 C、80 D、905. 如图，把圆分成六等分，经过各分点作圆的切线，以相邻切线的交点为顶点的图形是这个圆的外切正六边形， 的半径是R，它的外切正六边形的边长为（ ）
A、 B、 C、 D、6. 如图，BM是△ABC的角平分线，D是BC边上的一点，连接AD，使AD=DC，且∠BAD=120°，则∠AMB=（ ）
A、30° B、25° C、22.5° D、20°7. 如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为（ ）
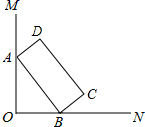A、 B、 C、 5 D、8. 如图，在 中， ∠ACB=90°， cm， cm. 是 边上的一个动点，连接 ，过点 作 于 ，连接 ，在点 变化的过程中，线段 的最小值是（ ）
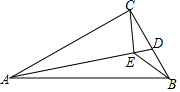A、1 B、 C、2 D、9. 如图，AB＝AD＝6，∠A＝60°，点C在∠DAB内部且∠C＝120°，则CB＋CD的最大值（ ）
A、4 B、8 C、10 D、610. 如图，一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合，且与边AB、CD相交于G、H．将多边形OGBCH的面积记为S，三条线段GB、BC、CH的长度之和记为l，在大正六边形绕点O旋转过程中，下列说法正确的是（ ）．
A、S变化，l不变 B、S不变，l变化 C、S变化，l变化 D、S与l均不变二、填空题
-
11. 如图，在△ABC中，点D、E分别是AB、AC边的中点，若BC＝6cm．刚线段DE＝cm．
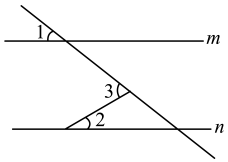
12. 如图，直线mn．若 ， ， 则的大小为度．
13. 如图，在△ABC中，∠B = 60°，∠C = 40°，AE平分∠BAC，AD⊥BC，垂足为点D，那么∠DAE =度．
14. 如图，在△ABC中，∠ACB为钝角，把边AC绕点A沿逆时针方向旋转90°得AD，把边BC绕点B沿顺时针方向旋转90°得BE，作DM⊥AB于点M，EN⊥AB于点N，若AB＝5，EN＝2，则DM＝.
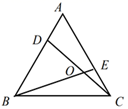
15. 如图，点 分别是等边三角形 的边 的点，且 与 相交于点 ．则 的度数为 ．
16. 如图，G为正方形ABCD的边AD上的一个动点，AE⊥BG，CF⊥BG，垂足分别为点E、F，已知AD=4，则AE2+CF2＝
17. 如图，在△ABC中，已知D，E，F分别为BC，AD，CE的中点，且S△ABC＝8cm2 ， 则图中阴影部分△BEF的面积等于cm2 ．
18. 如图， 为 的 边上的点、且 ，中线 被 截得的三线段为 ，则
三、综合题
-
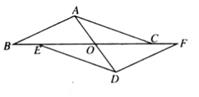
19. 如图，AD、BF相交于点O，点E、C在BF上，BE=FC，AC=DE，AB=DF，求证：四边形ABDF是平行四边形。
20. 如图，▱ABCD的对角线AC，BD相交于点O，点E、F在AC上，且AF=CE．求证：BE=DF．
21. 如图，在等腰 ABC中，AB=AC=6cm，∠B=30°，点D在BC边上由点C向点B匀速运动（点D不与点B ， C重合），速度为2cm/s，连接AD ， 作∠ADE=30°，DE交线段AC于点E ．
(1)、在此运动过程中，∠BDA逐渐变（填“大”或“小”）；D点运动到图1位置时，∠BDA=75°，则∠BAD=°．(2)、点D运动3s后到达图2位置，则CD=cm．此时 ABD和 DCE是否全等，请说明理由．(3)、在点D运动过程中， ADE的形状也在变化．当 ADE是等腰三角形时，∠BDA的度数为 ．22. 如图所示，△ABC是边长为6的等边三角形，P是AC边上一动点，由点A向点C运动(与A，C不重合)，Q是CB延长线上的一点，与点P同时以相同的速度由点B向CB延长线方向运动(Q不与B重合)，过点P作PE⊥AB于点E，连接PQ交AB于点D．
(1)、当∠BQD=30°时，求AP的长．(2)、试说明：在运动过程中，点D是线段PQ的中点．(3)、在运动过程中，线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化，请说明理由．23. 请阅读下列材料：问题：在四边形ABCD中，M是BC边的中点，且∠AMD=90°
(1)、如图1，若AB与CD不平行，试判断AB+CD与AD之间的数量关系；小雪同学的思路是：延长DM至E使DM=ME，连接AE，BE，构造全等三角形，经过推理使问题得到解决请你参考小雪的思路，在图1中把图形补充完整，并直接写出上面问题AB+CD与AD之间的数量关系：
(2)、如图2，若在原条件的基础上，增加AM平分∠BAD，（1）中结论还成立吗？若不成立，写出AB+CD与AD之间的数量关系，并证明．24. 如图1，△ABC和△DCE都是等边三角形.探究发现
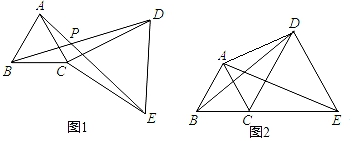(1)、△BCD与△ACE是否全等？若全等，加以证明；若不全等，请说明理由.拓展运用
(2)、若B、C、E三点不在一条直线上，∠ADC＝30°，AD＝3，CD＝2，求BD的长.(3)、若B、C、E三点在一条直线上（如图2），且△ABC和△DCE的边长分别为1和2，求△ACD的面积及AD的长.25.
(1)、如图①在 ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A=α，则∠BOC=（用α表示）；如图②∠CBO= ∠ABC，∠BCO= ∠ACB，∠A=α，则∠BOC=（用α表示）(2)、扩展探究：如图③，∠CBO= ∠DBC，∠BCO= ∠ECB，∠A=α，求∠BOC的度数（用α表示），并说明理由.
26. 如图
(1)、方法呈现：如图①：在 中，若 ， ，点D为BC边的中点，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使 ，再连接BE，可证 ，从而把AB、AC， 集中在 中，利用三角形三边的关系即可判断中线AD的取值范围是 ， 这种解决问题的方法我们称为倍长中线法；
(2)、探究应用：如图②，在 中，点D是BC的中点， 于点D，DE交AB于点E，DF交AC于点F，连接EF，判断 与EF的大小关系并证明；
(3)、问题拓展：如图③，在四边形ABCD中， ，AF与DC的延长线交于点F、点E是BC的中点，若AE是 的角平分线．试探究线段AB，AF，CF之间的数量关系，并加以证明．
27. 我们定义：如果一个三角形一条边上的高等于这条边，那么这个三角形叫做“等高底”三角形，这条边叫做这个三角形的“等底”.
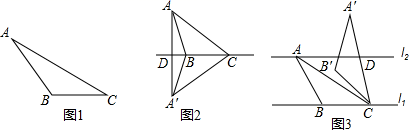(1)、概念理解：如图1，在△ABC中，AC＝6，DC＝3，∠ACB＝30°，试判断△ABC是否是“等高底”三角形.（填“是”或“否”）
(2)、问题探究：如图2，△ABC是“等高底”三角形，BC是“等底”，作△ABC关于BC所在直线的对称图形得到△A'BC，连接AA'交直线BC于点D.若点B是△AA′C的重心，求 的值.
(3)、应用拓展：如图3，已知l1∥l2 ， l1与l2之间的距离为2，“等高底”△ABC的“等底”BC在直线l1上，点A在直线l2上，有一边的长是BC的 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B′C，A′C所在直线交l2于点D，直接写出CD的值.
28.
(1)、问题发现：如图1，已知C为线段AB上一点，分别以线段AC、BC为直角边作等腰直角三角形，∠ACD=90°，CA=CD，CB=CE，连接AE、BD，则AE、BD之间的数量关系为；位置关系为.(2)、拓展探究：如图2，把Rt△ACD绕点C逆时针旋转，线段AE、BD交于点F，则 AE与 BD 之间的关系是否仍然成立?请说明理由.(3)、拓展延伸：如图3，已知AC=CD，BC=CE，∠ACD=∠BCE=90°，连接AB、AE、AD，把线段 AB绕点A旋转，若AB=5，AC=3，请直接写出旋转过程中线段AE的最大值.