吉林省白山市临江2021-2022学年七年级上学期期末考试数学试题

试卷更新日期：2022-01-17 类型：期末考试

进入出卷网下载

一、选择题（每小题2分，共12分）

1. 下列各数中，比-3小的数是（）

A、-5 B、-1 C、0 D、1

查看试题解析
2. 下列各单项式中，与-3x $y^{2}$ 是同类项的是（）

A、-2 $x^{2}$ y B、3 $y^{2}$ C、5x $y^{2}$ D、-6x

查看试题解析
3. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据计划“一带一路”地区覆盖总人口约为4400000000，这个数用科学记数法表示为（）

A、44× $1 0^{8}$ B、4.4× $1 0^{8}$ C、4.4× $1 0^{9}$ D、4.4× $1 0^{10}$

查看试题解析
4. 如果x=1是关于x的方程-x+a=3x-2 的解，则a的值为（）

A、1 B、-1 C、2 D、-2

查看试题解析
5. 如图，直线AB、CD相交于点O，OA平分∠EOC，∠EOC=70°，则∠BOE的度数是（）

A、145° B、135° C、35° D、120°

查看试题解析
6. 若|x|=7，|y|=5，且x+y>0，则x-y的值为（）

A、2或12 B、2或-12 C、-2或12 D、-2或-12

查看试题解析

二、填空题（每小题3分，共24分）

7. 若a+2的相反数是-5，则a=

查看试题解析
8. 将5.659用四舍五入法精确到0.1，取得的近似值为

查看试题解析
9. 若mn=m+3，则3m-3mn+10=

查看试题解析
10. 修建公路时，需要将弯曲的道路改直，用数学知识解释为

查看试题解析
11. 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如图是正方体的平面展开图，若图中的“锦”表示正方体的右面，则“”表示正方体的左面

查看试题解析
12. 一艘轮船在水中由A地开往B地，顺水航行用了4小时，由B地开往A地，逆水航行比顺水航行多用了1小时，已知此船在静水中速度是18千米/时，则水流速度为千米/时

查看试题解析
13. 如图，将一个三角板60°角的顶点与另一个三角板的直角顶点重合，∠1＝27°40′，则∠2的度数是

查看试题解析
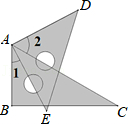14. 如图，由边长相等的黑、白两种颜色的正方形按照一定规律拼接而成，依此规律，第n个图案中白色正方形的个数为

查看试题解析

三、解答题（每小题5分，共20分）

15. 计算：- $2^{2}$ ×（-5）+32÷(-2)³

查看试题解析
16. 解方程 $\frac{2 x - 1}{3}$ +1＝ $\frac{2 x + 1}{6}$

查看试题解析
17. 先化简，再求值 5 $x^{2}$ +（4-5x-3 $x^{2}$ ）-（2x²-6x+5），其中x= -3

查看试题解析
18. 如图，已知线段a、b、∠O及内部一点P

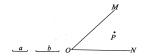
(1)、按下列要求画出图形（保留作图痕迹，不写作法）
①用无刻度的直尺和圆规在∠O的一条边OM上作线段OA=a，另一条边ON上作线段OB=a+b
②画出直线AB
③画射线OP与直线AB相交于点C

(2)、由（1）图形可知，在直线AB上，共有条射线

查看试题解析

四、解答题（每小题7分，共28分）

19. 如图，是由一些棱长为1cm的小正方体组成的简单几何体

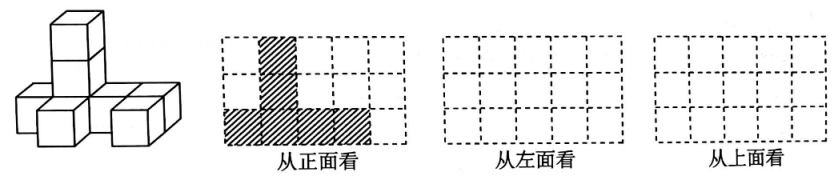(1)、请直接写出该几何体的表面积（含下底面）为

(2)、从正面看到的平面图形如图所示，请在下面方格中分别画出从左向右、从上向下看到的平面图形

查看试题解析
20. 如图

(1)、【观察思考】如图线段AB上有两个点C、D，分别以点A、B、C、D为端点的线段共有条

(2)、【模型构建】若线段上有m个点（包括端点），则该线段上共有条线段

(3)、【拓展应用】若有8位同学参加班级的演讲比赛，比赛采用单循环制（即每两位同学之间都要进行一场比赛），请你应用上述模型构建，求一共要进行多少场比赛？

查看试题解析
21. 若“△”表示一种新运算，规定a△b＝a×b﹣（a+b）

(1)、计算：（﹣4）△（﹣5）

(2)、已知（﹣2）△（1+x）＝﹣x+6，求x的值

查看试题解析
22. 如图，已知AB=24cm，BC= $\frac{3}{8}$ AB，点E是AC的中点，点D是AB的中点，求线段DE的长

查看试题解析

五、解答题（每题8分，共16分）

23. 为促进全民健身运动，某市组织了一次足球比赛，下表记录比赛过程中部分代表队的积分情况
代表队
场次（场）
胜（场）
平（场）
负（场）
积分（场）
A
6
5
1
0
16
B
6
6
0
0
18
C
6
3
2
1
11
D
6
3
1
2
10

(1)、本次比赛中，胜一场积分

(2)、若E代表队完成10场比赛后，只输了一场，积分是23分，请求出E代表队胜出的场数

查看试题解析
24. 题目：在同一平面上，若∠AOB＝70°，∠BOC＝15°，OE是∠AOC的平分线，求∠AOE的度数

解：由题知，可画出图（如图）
∵∠AOB＝70°，∠BOC＝15°∴∠AOC＝∠AOB﹣∠BOC＝70°﹣15°＝55°
又∵OE是∠AOC的平分线，∴∠AOE＝ $\frac{1}{2}$ ∠AOC＝ $\frac{1}{2}$ ×55°＝27.5°
以上是小明同学的解题过程，若你是老师，会判小马虎满分吗？若会，请说明理由；若不会，请指出小明同学的不符合题意，并将解题过程补充完整

查看试题解析

六、解答题（每题10分，共20分）

25. 为发展校园足球运动，学校决定购买一批足球运动装备，市场调查发现，甲、乙两商场以同样的价格出售同种品牌的足球和足球队服，已知每套队服比每个足球多50元，两套队服与三个足球的费用相等。经洽谈，甲商场优惠方案是：每购买十套队服，送一个足球；乙商场优惠方案是：若购买队服超过80套，则购买足球打八折

(1)、求每套队服和每个足球的价格是多少？

(2)、若购买100套队服和a（a＞10）个足球，请用含a的式子分别表示出甲商场和乙商场购买装备所花的费用。

(3)、在（2）的条件下，若a＝60，假如你是本次购买任务的负责人，你认为到甲、乙哪家商场购买比较合算？

查看试题解析
26. 如果两个角的差的绝对值等于90°，就称这两个角互为垂角，例如：∠1＝120°，∠2＝30°，|∠1﹣∠2|＝90°，则∠1和∠2互为垂角。（本题中所有角都是指大于0°且小于180°的角）

(1)、图1，O为直线AB上一点，∠AOC＝90°，∠EOD＝90°，则∠AOD垂角为和；

(2)、如果一个角的垂角等于这个角的补角的 $\frac{2}{3}$ ，求这个角的度数

(3)、图2，O为直线AB上一点，∠AOC＝90°，∠BOD＝30°，射线OC绕点O以9°/s的速度逆时针旋转，射线OD绕点O以6°/s的速度顺时针旋转，两条射线OC、OD同时运动，运动时间为ts（0＜t＜20），请直接写出当t的取值为时，∠AOC和∠AOD互为垂角？

查看试题解析

代表队	场次（场）	胜（场）	平（场）	负（场）	积分（场）
A	6	5	1	0	16
B	6	6	0	0	18
C	6	3	2	1	11
D	6	3	1	2	10