云南省开远市2021-2022学年上学期教学质量检测七年级期末数学试题

试卷更新日期：2022-01-17 类型：期末考试

进入出卷网下载

一、单选题

1. -3相反数是（）

A、 $\frac{1}{3}$ B、-3 C、 $- \frac{1}{3}$ D、3

查看试题解析
2. 开远1909广场就是为纪念滇越铁路开远段于1909年正式通车而修建的，广场集中展示了开远市的米轨历史文化，是集观光旅游、文化体验、度假休闲、游憩娱乐于一体的滇越文化深度体验旅游目的地，广场位于开远市凤凰生态公园凤凰山下，占地总面积14500平方米，是开远市打造的以米轨为主题的历史文化广场．数据14500用科学记数法表示为（）

A、14.5×10³ B、1.45×10⁴ C、145×10² D、0.145×10⁵

查看试题解析
3. 如图是一个正方体展开图，把展开图折叠成正方体后，“牢”字一面的相对面上的字是（）

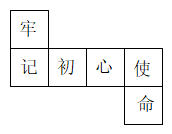A、初 B、心 C、使 D、命

查看试题解析
4. 下列结论正确的是（）

A、x =2是方程2x+1=4的解 B、单项式 $- \frac{2 π x}{3}$ 的系数是 $- \frac{2}{3}$ C、 $- 3 a b^{2}$ 和 $b^{2} a$ 是同类项 D、 $3 x^{2} - y + 5 x y^{2}$ 是二次三项式

查看试题解析
5. 下列等式的性质运用错误的是（）

A、如果a=b，那么a+2020=b+2020 B、如果a=b，那么-5a=-5b C、如果 $\frac{a}{c} = \frac{b}{c}$ ，那么a=b D、如果a=b，那么 $\frac{a}{c} = \frac{b}{c}$

查看试题解析
6. 在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（）

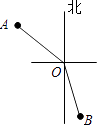A、69° B、111° C、141° D、159°

查看试题解析
7. 某车间28名工人生产螺栓和螺母，螺栓与螺母个数比为1：2刚好配套，每人每天平均生产螺栓12个或螺母18个，求多少人生产螺栓？设：有x名工人生产螺栓，其余人生产螺母.依题意列方程应为（）

A、12x＝18(28﹣x) B、2×12x＝18(28﹣x) C、12×18x＝18(28﹣x) D、12x＝2×18(28﹣x)

查看试题解析
8. 如图，一副三角板（直角顶点重合）摆放在桌面上，若∠AOD＝150°，则∠BOC等于（）

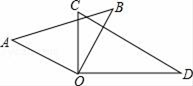A、30° B、45° C、50° D、60°

查看试题解析

二、填空题

9. 实数 $- 5 ， - 1 ， 0 ， \frac{1}{2}$ 四个数中,最大的数是.

查看试题解析
10. 已知∠α与∠β互余，且∠α=40°，则∠β的度数为．

查看试题解析
11. 若 $(x + 3)^{2} + | y - 2 | = 0$ ，则2x+y= ．

查看试题解析
12. 如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是．

查看试题解析
13. 已知点C是直线AB上一点，AB=6cm，BC=2cm，那么AC的长是．

查看试题解析
14. 如图，用相同的小正方形按照某种规律进行摆放，则第10个图形中小正方形的个数是个

查看试题解析

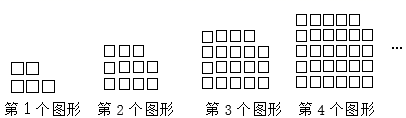
三、解答题

15. 计算：

(1)、 $- 2^{2} \times \frac{1}{4} - (- \frac{1}{2}) \times 4^{2}$ ；

(2)、 $3 \times (- 2) - | - 8 | \div (- 1) + {(- 1)}^{2020}$ ．

查看试题解析
16. 解方程：

(1)、 $3 (x - 2) - 4 = 5 x - 3$ ；

(2)、 $\frac{x - 1}{3} - \frac{x + 2}{6} = \frac{4 - x}{2}$ ．

查看试题解析
17. 先化简，再求值： $3 a^{2} - 2 (2 a^{2} + a) + 2 (a^{2} - 3 a)$ ，其中 $a = 2$ ．

查看试题解析
18. 如图，已知平面上有A、B、C、D四点，按下列语句要求画图：
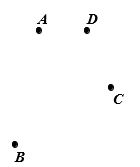
⑴画直线AD；
⑵画射线BC，射线BC与直线AD相交于点O；
⑶连接AC、BD，线段AC与线段BD相交于点F．

查看试题解析
19. 如图，延长线段AB到C，使BC＝3AB，点D是线段BC的中点，如果CD＝3cm，那么线段AC的长度是多少？

查看试题解析
20. 有8筐白菜，以每筐25千克为准，超过的千克数记作正数，不足的千克数记作负数，称后的记录如下：1.5，－3，2,－0.5,1,－2,－2,－2.5
问：这8筐白菜一共多少千克?

查看试题解析
21. 如图，OD是∠AOB的平分线，OE是∠BOC的平分线，且∠AOC=130°，求∠DOE的度数．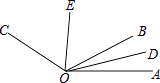

查看试题解析
22. 现政府大力提倡绿色、低碳出行，越来越多的人选择用电动车出行，某商场销售的一款电动车每台的标价是3270元，在一次促销活动中，按标价的八折销售，仍可盈利 $9 %$ .

(1)、求这款电动车每台的进价？ $($ 利润率 $= \frac{利润}{进价} = \frac{售价 - 进价}{进价}) .$

(2)、在这次促销活动中，商场销售了这款电动车100台，问盈利多少元？

查看试题解析
23. 如图，数轴的原点为O，点A、B、C是数轴上的三点，点B对应的数是1，AB=6，BC=2，动点P、Q同时分别从A、C出发，分别以每秒3个单位长度和每秒1个单位长度的速度沿数轴正方向运动．设运动时间为t秒（t＞0）．

(1)、点A表示的数为，点C表示的数为；

(2)、求t为何值时，点P与点Q重合？

(3)、是否存在某一时刻t，使点O平分线段PQ？若存在，请求出满足条件的t值；若不存在，请说明理由．

查看试题解析