吉林省四平市铁西区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-01-17 类型：期末考试

进入出卷网下载

一、单选题

1. 备受关注的北京环球度假区宣布将于2021年9月1日正式开启试运行，根据规划，北京环球影城建成后一期预计年接待游客超过1000万人次，将1000万用科学记数法表示为（）

A、 $0.1 \times 10^{4}$ B、 $1.0 \times 10^{3}$ C、 $1.0 \times 10^{6}$ D、 $1.0 \times 10^{7}$

查看试题解析
2. 下图是由5个大小相同的正方体组成的立体图形，其俯视图是（）

A、 B、 C、 D、

查看试题解析
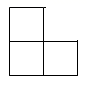3. 下列各组中的两个单项式中，是同类项的是（）

A、a²和－2a B、2m²n和3nm² C、－5ab和-5abc D、x³和2³

查看试题解析
4. 实效m，n在数轴上的对应点如图所示，则下列各式子正确的是（）

A、 $m > n$ B、 $- n > | m |$ C、 $- m > | n |$ D、 $| m | < | n |$

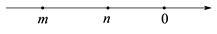查看试题解析
5. 如图，已知直线AB，CD相交于点O，OE平分∠COB，如果∠EOB＝55°，那么∠BOD的度数是（）

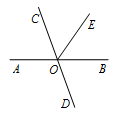A、35° B、55° C、70° D、110°

查看试题解析
6. 如图是某超市电子表的价格标签，一服务员不小心将墨水滴在标签上，使得原价看不清楚，请你帮助算一算，该电子表的原价是（）

A、21元 B、22元 C、23元 D、24元

查看试题解析

二、填空题

7. 计算 $33 ° 52 + 21 ° 54 =$ ．

查看试题解析
8. 在一面墙上用两根钉子钉木条时，木条就会固定不动，用数学知识解释这种生活现象为．

查看试题解析
9. 已知 $x = 2 y + 3$ ，则代数式 $4 x - 8 y + 9$ 的值是.

查看试题解析
10. 小明体重约为45.36千克，如果精确到0.1千克，其结果为千克．

查看试题解析
11. 如图，在数轴上，点A与点B之间表示整数的点有个．

查看试题解析
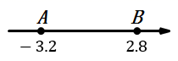12. 已知关于x的方程 $(a - 2) x = 9$ 与 $x + 1 = 4$ 的解相同，则a的值是．．

查看试题解析
13. 阅读框图，在四个步骤中，不是依据等式性质变形的是（填序号即可）．

查看试题解析
14.
如图，OA的方向是北偏东15°，OC的方向是北偏西40°，若∠AOC=∠AOB，则OB的方向是．

查看试题解析

三、解答题

15. 计算： $2 \times {(- 3)}^{2} - 4 \times (- 3) + 15$

查看试题解析
16. 计算： $1.5 - (- 4 \frac{1}{4}) + 3.75 - (+ 8 \frac{1}{2})$

查看试题解析
17. 解方程： $2 x - 10 = 2 (3 x - 1)$ ．

查看试题解析
18. 解方程： $\frac{2 x - 1}{2} - \frac{10 x + 1}{4} = 3$

查看试题解析
19. 一个角的补角比这个角的余角的3倍少50°，求这个角的度数．

查看试题解析
20. 以下是马小虎同学化简代数式 $(a^{2} b + 4 a b) - 3 (a b - a^{2} b)$ 的过程．
$(a^{2} b + 4 a b) - 3 (a b - a^{2} b)$
$= a^{2} b + 4 a b - 3 a b - 3 a^{2} b$ …第一步，
$= a^{2} b - 3 a^{2} b + 4 a b - 3 a b$ …第二步，
$= a b - 2 a^{2} b$ …第三步，

(1)、马小虎同学解答过程在第步开始出错，出错原因是；

(2)、请你帮助马小虎同学写出正确的解答过程．

查看试题解析
21. 如图， $A B = 10$ ，点C是线段AB的中点，点D是线段CB的中点，求AD的长．

查看试题解析
22. 某商店有两种书包，每个小书包比大书包的进价少25元，而它们的售后所获利润相同，其中，每个小书包的利润率为30%，每个大书包的利润率为20%，求两种书包的进价．

查看试题解析
23. 如图，平面上有四个点A，B，C，D．

(1)、根据下列语句画图：
①射线BA；
②直线AD，BC相交于点E；
③在线段DC的延长线上取一点F，使CF＝BC，连接EF．

(2)、图中以E为顶点的角中，小于平角的角共有个．

查看试题解析
24. 如图，以直线 $A B$ 上一点O为端点作射线 $O C$ ，使 $∠ A O C = 68 °$ ，在同一个平面内将一个直角三角板的直角顶点放在点O处．（注： $∠ D O E = 90 °$ ）

(1)、如图1，如果直角三角板 $D O E$ 的一边 $O D$ 放在射线 $O A$ 上，那么 $∠ C O E$ 的度数为；

(2)、如图2，将直角三角板 $D O E$ 绕点O按顺时针方向转动到某个位置，如果 $O C$ 恰好平分 $∠ A O E$ ，求 $∠ C O D$ 的度数：

(3)、如图3，将直角三角板 $D O E$ 绕点O任意转动，如果 $O D$ 始终在 $∠ A O C$ 的内部，请直接用等式表示 $∠ A O D$ 和 $∠ C O E$ 之间的数量关系．

查看试题解析
25. 某信息管理中心，在距下班还剩4小时的时候，接到将一批工业最新动态信息输入管理储存网络的任务，甲单独做需6小时完成，乙单独做需4小时完成：

(1)、甲乙合作需要小时完成?

(2)、若甲先做30分钟，然后甲、乙合作，则甲、乙合作还需多少小时才能完成工作?

(3)、若甲先做30分钟，然后甲、乙合作1小时，这时又接到新的工作任务，必须调走一人，问剩下那人能否在下班之前完成这项工作?

查看试题解析
26. 如图，A，B是数轴上两点，点B表示的数为3， $A B = 6$ ，

(1)、在数轴上，点A表示的数为；

(2)、现有动点P、Q都在A点处，先是点P以每秒1个单位长度的速度向右匀速移动：此时点Q停留在点A处不动，当点P移动到原点O时，点Q才从A点出发，并以每秒3个单位长度的速度向右匀速移动，设点P的运动时间为 $t (t > 0)$ ．
①在数轴上，点P表示的数为 ▲ ，当点Q出发后，点Q表示的数为 ▲ ；（用含t的代数式表示）
②请求出当t为多少时，点P与点Q重合；
③请直接写出当t为多少时， $O Q = 2 O P$ ．

查看试题解析