吉林省四平市双辽市2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-01-17 类型：期末考试

进入出卷网下载

一、单选题

1. -2的相反数是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. -3在数轴上位置的描述，正确的是（）

A、在点-4的左边 B、在点-2和原点之间 C、由点1向左平移4个单位得到 D、和原点的距离是-3

查看试题解析
3. 已知单项式 $5 x^{2} y^{a - 2}$ 的次数是3，则 $a$ 的值是（）

A、3 B、4 C、5 D、6

查看试题解析
4. 将一堆糖果分给幼儿园的小朋友，如果每人2颗，那么就多4颗；如果每人3颗，那么就少6颗．设有糖果 $x$ 颗，则可得方程为（）

A、 $\frac{x - 4}{2} = \frac{x + 6}{3}$ B、 $2 x + 4 = 3 x - 6$ C、 $\frac{x - 4}{3} = \frac{x + 6}{2}$ D、 $\frac{x + 4}{2} = \frac{x - 6}{3}$

查看试题解析
5. 如图所示，OA是北偏东30°方向的一条射线，若∠AOB＝90°，则OB的方位角是（）

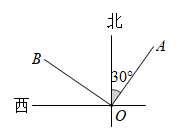A、北偏西30° B、北偏西60° C、北偏东30° D、北偏东60°

查看试题解析
6. 下列说法正确的个数是（）
①平方等于本身的数是正数；②单项式﹣π²x³y²的次数是7；③近似数7与7.0的精确度不相同；④因为a＞b，所以|a|＞|b|；⑤一个角的补角大于这个角本身．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 某市一天最高气温是 $10 ℃$ ，最低气温是 $- 1 ℃$ ，则这天的日温差是℃．

查看试题解析
8. 比较大小：﹣| $- \frac{1}{4}$ |﹣（ $- \frac{1}{4}$ ）．（填“＞”、“＜”或“＝”）．

查看试题解析
9. 计算：﹣2³+（﹣ $\frac{1}{2}$ ）³＝.

查看试题解析
10. 若代数式 $\frac{2 x - 1}{3}$ 与x－3互为相反数，则x＝；

查看试题解析
11. 如图是一个正方体的展开图，把它折叠成正方体后，有“学”字一面的相对面上的字是．

查看试题解析
12. 如图所示，一副三角板（直角顶点重合）摆放在桌面上，若∠AOC＝125°，则∠BOD的度数为．

查看试题解析
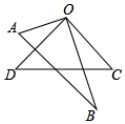13. 如图，点A、B在直线l上，点C是直线l外一点，可知CA+CB＞AB，其依据是．

查看试题解析
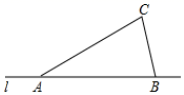14. 如图，过直线AB上一点O作射线OC，∠BOC＝29°38′，OD平分∠AOC，则∠DOC的度数为．

查看试题解析

三、解答题

15. 计算：4﹣（ $\frac{2}{3} - 2 \frac{1}{4} - 2 \frac{5}{6}$ ）×（﹣12）．

查看试题解析
16. 先化简，再求值：2（2x²y+9y）﹣3（5x²y﹣4y），其中x＝﹣2，y＝1．

查看试题解析
17. 解方程： $\frac{4 x - 1}{6} =$ 1 $- \frac{3 x - 1}{3}$ ．

查看试题解析
18. 已知：如图，点C为线段AB的中点，点E为线段AB上的点，点D为线段AE的中点，若线段AB=15，CE=4.5，求线段BE、DE的长.

查看试题解析
19. A，B两果园分别有橘子50吨和60吨，按四条线路，将橘子全部运送到C，D两地，C，D两地分别运到橘子40吨和70吨，已知从A，B两果园到C，D两地的运价标准如下表：

到C地的运价
到D地的运价
A果园
每吨8元
每吨10元
B果园
每吨7元
每吨11元

(1)、设从A果园运到C地的橘子为x（ $0 < x < 40$ ）吨．
①请直接写出从A果园运到D地的橘子为 ▲ 吨，从B果园运到C地的橘子为 ▲ 吨（用含x的代数式表示）；
②求四条线路运输橘子的总运输费（用含x的代数式表示）；

(2)、当从A果园运到D地的橘子为15吨时，请直接写出四条线路运输橘子的总运输费为．

查看试题解析
20. 对于方程 $\frac{x}{3} - \frac{x - 1}{2} = 1$ ，某同学解法如下：
解：方程两边同乘6，得2x－3（x－1）＝1①
去括号，得2x－3x－3＝1②
合并同类项，得－x－3＝1③
移项，得－x＝4④
∴x＝－4⑤

(1)、上述解答过程从第步开始出现错误；

(2)、请写出正确的解答过程．

查看试题解析
21. 如图，已知点A，B，C，D，根据下列语句，按要求画出图形．
①画线段AB，射线AD，直线AC；
②连接BD与直线AC交于点E；
③连接BC，并延长线段BC与射线AD交于点F；
④连接CD，并延长线段CD与线段AB的反向延长线交于点G．

查看试题解析
22. 如图，点O为直线AB上的一点，已知∠1＝65°15′，∠2＝78°30′，求∠1+∠2﹣∠3的大小．

查看试题解析
23.

(1)、画出数轴，用数轴上的点表示下列各数，并用“＞”将它们连接起来：﹣3，﹣1.75，1，﹣0.5，

(2)、数轴上点A表示的数为﹣3时绝对值，点B表示的数为1的相反数，点P从点A出发，以每秒5个单位长度的速度沿数轴向正方向匀速运动，同时点Q从点B出发，以每秒4个单位长度的速度沿数轴向负方向匀速运动，当运动时间为5秒时，请直接写出点P表示的数为，点Q表示的数为，点P和点Q之间的距离为个单位长度．

查看试题解析
24. 两船从同一港口同时出发反向而行，甲船顺水，乙船逆水，两船在静水中的速度都是50km/h，水流速度是akm/h．

(1)、2h后两船相距多远？

(2)、2h后甲船比乙船多航行多少千米？

(3)、一艘小快艇送游客在甲、乙两个码头间往返，其中去程的时间是回程的时间3倍，则小快艇在静水中的速度v与水流速度a的关系是．

查看试题解析
25. 如图

(1)、已知：如图1所示，已知∠AOC＝90°，∠AOB＝38°，OD平分∠BOC，请判断∠AOD和∠BOD之间的数量关系，并说明理由；

(2)、已知：如图2，点O在直线AD上，射线OC平分∠BOD．请判断∠AOC与∠BOC之间的数量关系，并说明理由；

(3)、已知：如图3，∠EPQ和∠FPQ互余，射线PM平分∠EPQ，射线PN平分∠FPQ．直接写出锐角∠MPN的度数是．

查看试题解析
26. 某工厂车间有28个工人，生产零件和零件，每人每天可生产A零件18个或B零件12个（每人每天只能生产一种零件），一个A零件配两个B零件，且每天生产的A零件和B零件恰好配套．工厂将零件批发给商场时，每个A零件可获利10元，每个B零件可获利5元．

(1)、求该工厂有多少工人生产A零件？

(2)、因市场需求，该工厂每天要多生产出一部分A零件供商场零售使用，现从生产B零件的工人中调出多少名工人生产A零件，才能使每日生产的零件总获利比调动前多600元？

查看试题解析

	到C地的运价	到D地的运价
A果园	每吨8元	每吨10元
B果园	每吨7元	每吨11元