黑龙江省鸡西市虎林市2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-01-17 类型:期末考试
一、单选题
-
1. 下面四个图形中,∠1=∠2一定成立的是( )A、
 B、
B、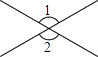 C、
C、 D、
D、 2. 已知 ,则下列不等式一定成立的是( )A、 B、 C、 D、3. 以下说法正确的是( )A、同旁内角互补 B、有公共顶点、并且相等的两个角是对顶角 C、经过直线外一点,有且只有一条直线与这条直线平行 D、如果两个角之和等于 ,那么这两个角是互为邻补角4. 为了交接某校2000名学生的数学成绩,抽取了其中50名学生的数学成绩进行整理分析,这个调查过程中的样本是( )A、2000名学生的数学成绩 B、2000 C、被抽取的50名学生的数学成绩 D、505. 若关于x的不等式组 无解,则实数a的取值范围是( )A、 B、 C、 D、6. 如图,把水渠中的水引到水池 ,先过 点向渠岸 画垂线,垂足为 ,再沿垂线 开沟才能使沟最短,其依据是( )
2. 已知 ,则下列不等式一定成立的是( )A、 B、 C、 D、3. 以下说法正确的是( )A、同旁内角互补 B、有公共顶点、并且相等的两个角是对顶角 C、经过直线外一点,有且只有一条直线与这条直线平行 D、如果两个角之和等于 ,那么这两个角是互为邻补角4. 为了交接某校2000名学生的数学成绩,抽取了其中50名学生的数学成绩进行整理分析,这个调查过程中的样本是( )A、2000名学生的数学成绩 B、2000 C、被抽取的50名学生的数学成绩 D、505. 若关于x的不等式组 无解,则实数a的取值范围是( )A、 B、 C、 D、6. 如图,把水渠中的水引到水池 ,先过 点向渠岸 画垂线,垂足为 ,再沿垂线 开沟才能使沟最短,其依据是( ) A、垂线段最短 B、过一点确定一条直线与已知直线垂直 C、垂线最短 D、以上说法都不对7. 一个正方形的面积是15,估计它的边长大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间8. 在平面直角坐标系中,若过不同的两点P(2a,6)与Q(4+b,3-b)的直线PQ∥x轴,则( )A、a= , b=-3 B、a≠ , b≠-3 C、a= , b≠-3 D、a≠ , b=-39. 某次数学竞赛共有 20 道题,答对一道题得 10 分,答错或不答均 扣5 分,小强得分超过 95 分,他至少要答对( )A、12 道 B、13 道 C、14 道 D、15 道10. 如图,AD是△ABC的中线,E , F分别是AD和AD延长线上的点,且DE=DF , 连接BF , CE . 下列说法①△BDF≌△CDE;②△ABD和△ACD面积相等;③BF∥CE;④CE=BF . 其中正确的有( )
A、垂线段最短 B、过一点确定一条直线与已知直线垂直 C、垂线最短 D、以上说法都不对7. 一个正方形的面积是15,估计它的边长大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间8. 在平面直角坐标系中,若过不同的两点P(2a,6)与Q(4+b,3-b)的直线PQ∥x轴,则( )A、a= , b=-3 B、a≠ , b≠-3 C、a= , b≠-3 D、a≠ , b=-39. 某次数学竞赛共有 20 道题,答对一道题得 10 分,答错或不答均 扣5 分,小强得分超过 95 分,他至少要答对( )A、12 道 B、13 道 C、14 道 D、15 道10. 如图,AD是△ABC的中线,E , F分别是AD和AD延长线上的点,且DE=DF , 连接BF , CE . 下列说法①△BDF≌△CDE;②△ABD和△ACD面积相等;③BF∥CE;④CE=BF . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 把命题“同角的余角相等”改写成“如果…那么…”的形式 .12. 计算: = .13. 如图,请你添加一个条件使得AD∥BC , 所添的条件是 .
 14. 某中学要了解八年级学生的视力情况,在全校八年级学生中抽取了25名学生进行检测,在这个问题中,总体是 , 样本是 .15. 已知在平面直角坐标系中,点 在第二象限,且到 轴的距离为3,到 轴的距离为4,则点 的坐标为 .16. 在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动,属于平移现象的有(只填序号)17. 已知 ,则 的值是 .18. 甲、乙两地相距 100 千米,一艘轮船往返两地,顺流用 4 小时,逆流用 5 小时,那么这艘轮船在静水中的速度是千米/时.19. 把方程组 中,若未知数 满足 ,则 的取值范围是.20. 在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2 , 点A2的伴随点为A3 , 点A3的伴随点为A4 , …,这样依次得到点A1 , A2 , A3 , …,An , ….若点A1的坐标为(3,1),则点A2的坐标为 , 点A2 019的坐标为;若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
14. 某中学要了解八年级学生的视力情况,在全校八年级学生中抽取了25名学生进行检测,在这个问题中,总体是 , 样本是 .15. 已知在平面直角坐标系中,点 在第二象限,且到 轴的距离为3,到 轴的距离为4,则点 的坐标为 .16. 在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动,属于平移现象的有(只填序号)17. 已知 ,则 的值是 .18. 甲、乙两地相距 100 千米,一艘轮船往返两地,顺流用 4 小时,逆流用 5 小时,那么这艘轮船在静水中的速度是千米/时.19. 把方程组 中,若未知数 满足 ,则 的取值范围是.20. 在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2 , 点A2的伴随点为A3 , 点A3的伴随点为A4 , …,这样依次得到点A1 , A2 , A3 , …,An , ….若点A1的坐标为(3,1),则点A2的坐标为 , 点A2 019的坐标为;若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .三、解答题
-
21.(1)、解方程组:(2)、解不等式组22. 已知 的平方根是 , 的立方根是 ,求 的算术平方根23. 如图,在平面直角坐标系中,三角形ABC的顶点坐标分别是A(-4,-1),B(1,1),C(-1,4),点P(x1 , y1)是三角形ABC内一点,点P(x1 , y1)平移到点P1(x1+3,y1-1)时;
 (1)、画出平移后的新三角形A1B1C1并分别写出点A1B1C1的坐标;(2)、求出三角形A1B1C1的面积.24. 如图,直线AB,CD相交于点O,OE平分∠BOC,FO⊥CD于点O,若∠BOD∶∠EOB=2∶3,求∠AOF的度数.
(1)、画出平移后的新三角形A1B1C1并分别写出点A1B1C1的坐标;(2)、求出三角形A1B1C1的面积.24. 如图,直线AB,CD相交于点O,OE平分∠BOC,FO⊥CD于点O,若∠BOD∶∠EOB=2∶3,求∠AOF的度数.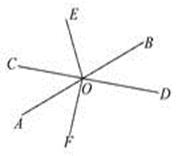 25. 某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
25. 某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.组别
符合题意字数
人数
10
15
25

根据以上信息解决下列问题:
(1)、在统计表中, , ;并补全条形统计图 .(2)、扇形统计图中“组”所对应的圆心角的度数;(3)、若该校共有名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
