2021-2022学年苏科版数学七年级下册7.5多边形的内角和与外角和同步练习(基础)
试卷更新日期:2022-01-17 类型:同步测试
一、单选题
-
1. 下列条件中,能判定 为直角三角形的是( )A、 B、 C、 D、2. 正五边形的内角和是( )A、 B、 C、 D、3. 如果将一副三角板按如图方式叠放,那么 的度数是( )
 A、 B、 C、 D、4. AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD= ( )
A、 B、 C、 D、4. AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD= ( )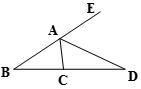 A、25° B、60° C、85° D、95°5. 如果一个多边形的每个外角都是36°,那么这个多边形的边数是( )A、5 B、6 C、10 D、126. “花影遮墙,峰峦叠窗”苏州园林空透的窗棂中蕴含着许多的数学元素.如图是窗棂是冰裂纹窗及这种窗棂中的部分图案.若 , ,则下列判断中正确的是( )
A、25° B、60° C、85° D、95°5. 如果一个多边形的每个外角都是36°,那么这个多边形的边数是( )A、5 B、6 C、10 D、126. “花影遮墙,峰峦叠窗”苏州园林空透的窗棂中蕴含着许多的数学元素.如图是窗棂是冰裂纹窗及这种窗棂中的部分图案.若 , ,则下列判断中正确的是( ) A、 B、 C、 D、 的度数无法确定7. 若多边形的边数增加一条,则它的外角和( )A、增加180° B、不变 C、增加360° D、减少180°8. 将一副直角三角板如图所示放置,使含 角的三角板的一条直角边和含 角的三角板的一条直角边在同一条直线上,则 的度数为( )
A、 B、 C、 D、 的度数无法确定7. 若多边形的边数增加一条,则它的外角和( )A、增加180° B、不变 C、增加360° D、减少180°8. 将一副直角三角板如图所示放置,使含 角的三角板的一条直角边和含 角的三角板的一条直角边在同一条直线上,则 的度数为( )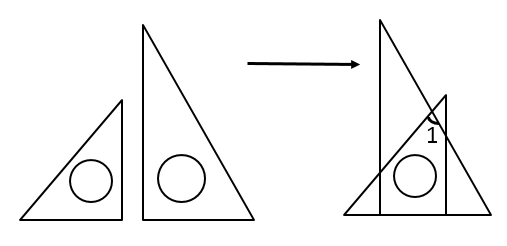 A、 B、 C、 D、9. 如图,小明在操场上从A点出发,沿直线前进10米后向左转 ,再沿直线前进10米后,又向左转 ,这样走下去,他第一次回到出发地A点时,一共走了( )米
A、 B、 C、 D、9. 如图,小明在操场上从A点出发,沿直线前进10米后向左转 ,再沿直线前进10米后,又向左转 ,这样走下去,他第一次回到出发地A点时,一共走了( )米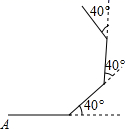 A、70 B、80 C、90 D、100
A、70 B、80 C、90 D、100二、填空题
-
10. 在 中, , ,则 为.11. 在 中, ,则 等于.12. 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D.若∠A=32°,则∠BCD=°.
 13. 如图,在锐角三角形ABC中,CD和BE分别是AB和AC边上的高, 且CD和BE交于点P,若∠A=40º,则∠BPC的度数是.
13. 如图,在锐角三角形ABC中,CD和BE分别是AB和AC边上的高, 且CD和BE交于点P,若∠A=40º,则∠BPC的度数是. 14. 已知:如图,在△ABC中,∠A=55
14. 已知:如图,在△ABC中,∠A=55 ,H是高BD、CE的交点,则∠BHC=.
,H是高BD、CE的交点,则∠BHC=.  15. 在一个三角形中,如果一个内角是另一个内角的2倍,那么这个三角形称为理想三角形;如果一个内角是另一个内角的3倍,那么这个三角形称为梦想三角形.若一个三角形既是理想三角形,也是梦想三角形,写出这个三角形的三个内角的度数(只写出一组).16. 如图,∠1+∠2+∠3+∠4=度.
15. 在一个三角形中,如果一个内角是另一个内角的2倍,那么这个三角形称为理想三角形;如果一个内角是另一个内角的3倍,那么这个三角形称为梦想三角形.若一个三角形既是理想三角形,也是梦想三角形,写出这个三角形的三个内角的度数(只写出一组).16. 如图,∠1+∠2+∠3+∠4=度.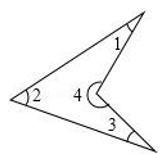
三、解答题
-
17. 如图,DE⊥AB,EF∥AC,∠A=32°,
①求∠DEF的度数;
②若∠F比∠ACF大60°,求∠B的度数.
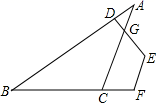 18. 如图,已知:AD平分∠BAC,点E是AD反向延长线上的一点,EF⊥BC,∠1=40°,∠C=65°.求:∠B和∠E的度数.
18. 如图,已知:AD平分∠BAC,点E是AD反向延长线上的一点,EF⊥BC,∠1=40°,∠C=65°.求:∠B和∠E的度数. 19. 如图,在△ABC中,BE是AC边上的高,DE∥BC,∠ADE=48°,∠C=62°,求∠ABE的度数.
19. 如图,在△ABC中,BE是AC边上的高,DE∥BC,∠ADE=48°,∠C=62°,求∠ABE的度数.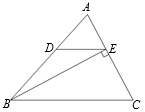 20. 如图,已知AB∥CD.若∠ABE=75°,∠CDE=60°,求∠E的度数.
20. 如图,已知AB∥CD.若∠ABE=75°,∠CDE=60°,求∠E的度数.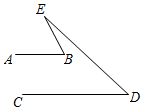 21. 如图,在 中, 平分 交 于点 , 是 的边 上的高且 , ,
21. 如图,在 中, 平分 交 于点 , 是 的边 上的高且 , ,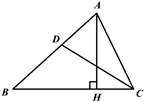 (1)、直接写出 .(2)、求 的度数.22. 如图,CD是△ABC的角平分线,点E是AC边上的一点, .
(1)、直接写出 .(2)、求 的度数.22. 如图,CD是△ABC的角平分线,点E是AC边上的一点, . (1)、求证: ;(2)、 , ,求∠DEC的度数.23. 如图,在△ABC中,D为AC边上一点,∠A=∠ABD,∠C=∠CBD.
(1)、求证: ;(2)、 , ,求∠DEC的度数.23. 如图,在△ABC中,D为AC边上一点,∠A=∠ABD,∠C=∠CBD. (1)、求∠ABC的度数;(2)、若DE平分∠ADB交AB于点E,求证:DE∥BC.24. 如图,在 中, 是高, 是角平分线, , .
(1)、求∠ABC的度数;(2)、若DE平分∠ADB交AB于点E,求证:DE∥BC.24. 如图,在 中, 是高, 是角平分线, , .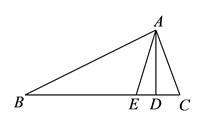 (1)、求 、 和 的度数.(2)、若图形发生了变化,已知的两个角度数改为:当 , ,则 .
(1)、求 、 和 的度数.(2)、若图形发生了变化,已知的两个角度数改为:当 , ,则 .当 , 时,则 .
当 , 时,则 .
当 , 时,则 .
25. 如图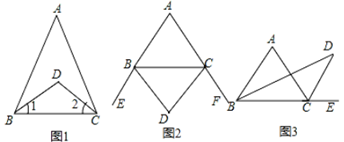 (1)、如图1所示,BD,CD分别是△ABC的内角∠ABC,∠ACB的平分线,试说明:∠D=90°+ ∠A.(2)、探究,请直接写出下列两种情况的结果,并任选一种情况说明理由:
(1)、如图1所示,BD,CD分别是△ABC的内角∠ABC,∠ACB的平分线,试说明:∠D=90°+ ∠A.(2)、探究,请直接写出下列两种情况的结果,并任选一种情况说明理由:①如图2所示,BD,CD分别是△ABC两个外角∠EBC和∠FCB的平分线,试探究∠A与∠D之间的等量关系;
②如图3所示,BD,CD分别是△ABC一个内角∠ABC和一个外角∠ACE的平分线,试探究∠A与∠D之间的等量关系.