湘教版初中数学七年级下册1.4三元一次方程组同步练习

试卷更新日期：2022-01-16 类型：同步测试

进入出卷网下载

一、单选题

1. 6月18日最开始是京东的周年庆，相当于淘宝的双十一活动，在2013年之前，京东就将每年的6月18日定为年庆。2013年后，618就成了各大电商平台的网购节了。在618当日，小李在某电商平台上选择了甲乙丙三种商品，当购物车内选3件甲，2件乙，1件丙时显示价格为420元；当选2件甲，3件乙，4件丙时显示价格为580元，那么购买甲、乙、丙各一件时应该付款（）

A、580元 B、500元 C、420元 D、200元

查看试题解析
2. 若 $2 x + 5 y - 3 z = 2$ ， $3 x + 8 z = 3$ ，则x＋y＋z的值等于（）

A、0 B、2 C、1 D、无法求出

查看试题解析
3. 甲、乙、丙三种商品，若购买甲2件、乙4件、丙3件，共需220元钱，购甲3件、乙1件、丙2件共需235元钱，那么购甲、乙、丙三种商品各一件共需（）

A、85元 B、89元 C、90元 D、91元

查看试题解析
4. 若实数 $x ， y ， z$ 满足 ${\begin{array}{l} x - y + 4 z = 1 \\ x - 2 y + 3 z = 3 \end{array}$ ，则 $x + y + 6 z =$ （）

A、 $- 3$ B、 $0$ C、 $3$ D、不能确定值

查看试题解析
5. 方程组 ${\begin{cases} 3 x - 2 y = 5 \\ x + y + z = 2 \\ z = 2 \end{cases}$ 的解是（）

A、 ${\begin{cases} x = 1 \\ y = 1 \\ z = 2 \end{cases}$ B、 ${\begin{cases} x = 1 \\ y = - 1 \\ z = 2 \end{cases}$ C、 ${\begin{cases} x = - 1 \\ y = 1 \\ z = 2 \end{cases}$ D、 ${\begin{cases} x = - 1 \\ y = - 1 \\ z = 2 \end{cases}$

查看试题解析
6. 为确保信息安全，信息需要加密传输，发送方由明文→密文（加密）（解密），接收方由密文→明文（解密），已知加密规则为：明文a，b，c，对应密文a+1，-a+2b+4，b+3c+9，如果接收方收到密文7，12，22，则解密得到的明文为（）

A、6，2，7 B、2，6，7 C、6，7，2 D、7，2，6

查看试题解析
7. 在抗击疫情网络知识竞赛中，为奖励成绩突出的学生，学校计划用200元钱购买A、B、C三种奖品，A种每个10元，B种每个20元，C种每个30元，在C种奖品不超过两个且钱全部用完的情况下，购买方案有（）

A、12种 B、14种 C、15种 D、16种

查看试题解析
8. 小明和小亮在一起探究一个数学活动.首先小亮站立在箱子上，小明站立在地面上（如图1），然后交换位置（如图2），测量的数据如图所示，想要探究的问题有：①小明的身高；②小亮的身高；③箱子的高度；④小明与小亮的身高和.根据图上信息，你认为可以计算出的是（）

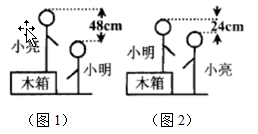A、① B、② C、③ D、④

查看试题解析
9. 设“●■▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，如果要使第三架天平也平衡，那么“？”处应该放“●”的个数为（）

A、4 B、3 C、2 D、1

查看试题解析
10. 如图所示，两个天平都平衡，则三个苹果的重量等于多少个香蕉的重量？答（）个.

A、2 B、3 C、4 D、5

查看试题解析
11. 如果二元一次方程组 ${\begin{cases} x - y = a \\ x + y = 3 a \end{cases}$ 的解是二元一次方程3x﹣5y﹣7=0的一个解，那么a值是（）

A、3 B、5 C、7 D、9

查看试题解析
12. 如果 ${\begin{cases} x + 2 y - 8 z = 0 \\ 2 x - 3 y + 5 z = 0 \end{cases}$ ，其中xyz≠0，那么x：y：z=（）

A、1：2：3 B、2：3：4 C、2：3：1 D、3：2：1

查看试题解析

二、填空题

13. 购买铅笔7支，作业本3本，圆珠笔1支共需3元；购买铅笔10支，作业本4本，圆珠笔1支共需4元，则购买铅笔11支、作业本5本，圆珠笔2支共需元．

查看试题解析
14. 若4x﹣3y﹣6z=0，x+2y﹣7z=0（xyz≠0），则 $\frac{5 x^{2} + 2 y^{2} - z^{2}}{2 x^{2} - 3 y^{2} - 10 z^{2}}$ 的值等于．

查看试题解析
15. 山脚下有一池塘，泉水以固定的流量（即单位时间里流入池中的水量相同）不停地向池塘内流淌．现池塘中有一定深度的水，若用一台A型抽水机抽水，则1小时正好能把池塘中的水抽完；若用两台A型抽水机抽水，则20分钟正好把池塘中的水抽完．问若用三台A型抽水机同时抽，则需要分钟恰好把池塘中的水抽完．

查看试题解析
16. 确保信息安全，信息需加密传输，发送方由明文 $\Rightarrow$ 密文（加密），接收方由密文 $\Rightarrow$ 明文（解密），已知加密规则为：明文a ， b ， c ， d对应密文a＋2b ， 2b＋c ， 2c＋3d ， 4d ．例如，明文1，2，3，4对应密文5，7，18，16.当接收方收到密文14，9，23，28时，则解密得到的明文为．

查看试题解析
17. 已知非负数a,b,c满足条件3a+2b+c=4. 2a+b+3c=5. 设s=5a+4b+7c的最大值为m，最小值为n．则n-m的值为.

查看试题解析
18. 我市某重点中学校团委、学生会发出倡议，在初中各年级捐款购买书籍送给我市贫困地区的学校．初一年级利用捐款买甲、乙两种自然科学书籍若干本，用去5324元；初二年级买了A、B两种文学书籍若干本，用去4840元，其中A、B的数量分别与甲、乙的数量相等，且甲种书与B种书的单价相同，乙种书与A种书的单价相同．若甲、乙两种书的单价之和为121元，则初一和初二两个年级共向贫困地区的学校捐献了本书．

查看试题解析
19. 在△ABC中，∠A－∠C＝25°，∠B－∠A＝10°，则∠B＝．

查看试题解析
20. 若x＋y＋z＝15，－3x－y＋z＝－25，x、y、z皆为非负数，记整式5x+4y+z的最大值为a，最小值为b，则a﹣b =.

查看试题解析
21. 小红到超市购买钢笔、笔记本、圆珠笔发现：若购买3支钢笔、7个笔记本、1支圆珠笔共需315元；若购买4支钢笔、10个笔记本、1支圆珠笔，共需420元钱．现若只购买2支钢笔、6个笔记本，共需元钱．

查看试题解析
22. 设 ${\begin{array}{l} 2 x + y + 3 z = 23 \\ x + 4 y + 5 z = 36 \end{array}$ ，则3x-2y+z= ．

查看试题解析

三、计算题

23. $\{\begin{matrix} x + 2 y + 3 z = 15 \\ \frac{x + 4 z}{3} = \frac{y - 3 z}{4} = 3 \end{matrix}$

查看试题解析
24. ${\begin{matrix} \begin{matrix} 2 x - 3 y + 4 z = 12 \\ x - y + 3 z = 4 \end{matrix} \\ 4 x + y - 3 z = - 2 \end{matrix}$

查看试题解析
25. ${\begin{matrix} x ： y ： z = 1 ： 3 ： 5 \\ x + y + z = 18 \end{matrix}$

查看试题解析
26. ${\begin{matrix} \frac{x}{3} = \frac{y}{2} = \frac{z}{5} \\ 2 x + 3 y - 4 z = 8 \end{matrix}$

查看试题解析

四、解答题

27. 一个三位数，个位，百位上的数字的和等于十位上的数字，百位上的数字的7倍比个位，十位上的数字的和大2，个位，十位，百位上的数字的和是14，求这个三位数.

查看试题解析
28. ${\begin{matrix} \begin{matrix} x = - 1 \\ y = 1 \end{matrix} \\ z = 2 \end{matrix}$ 是关于x、y、z的方程 $| a x + b y + 2 | + {(a y + c z - 1)}^{2} + | b z + c x - 3 | = 0$ 的一个解．试求a、b、c的值．

查看试题解析
29. 利用两块完全相同的长方形木块测量一张桌子的高度，首先将木块按图一方式放置，再交换两木块的位置，按图二方式放置，测量数据如图，求桌子的高度.

查看试题解析

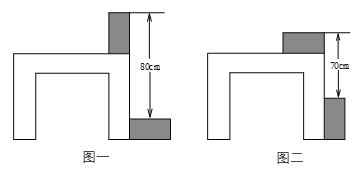
五、综合题

30. 某商场计划用56000元从厂家购进60台新型电子产品，已知该厂家生产甲乙、丙三种不同型号的电子产品，设甲、乙型设备应各买入x，y台，其中每台的价格、销售获利如下表：

甲型

乙型

丙型

价格(元/台)

1000

800

500

销售获利(元/台)

260

190

120

(1)、购买丙型设备台(用含x，y的代数式表示)；

(2)、若商场同时购进三种不同型号的电子产品(每种型号至少有一台)，恰好用了56000元，则商场有哪几种购进方案？

(3)、在第(2)题的基础上，为了使销售时获利最多，应选择哪种购进方案？此时获利为多少？

查看试题解析
31. 某工程由甲、乙两队合作需6天完成，厂家需付甲、乙两队共8700元，乙、丙两队合作需10天完成，厂家需支付乙、丙两队共9500元；甲、丙两队合作5天完成全部工程的 $\frac{2}{3}$ ，此时厂家需付甲、丙两队共5500元．

(1)、求甲、乙、丙各队单独完成全部工程各需多少天？

(2)、若要不超过15天完成全部工程，问由哪队单独完成此项工程花钱最少？请说明理由

查看试题解析
32. 某学校计划用104 000元购置一批电脑（这批款项须恰好用完，不得剩余或追加）．经过招标，其中平板电脑每台1600元，台式电脑每台4000元，笔记本电脑每台4600元．

(1)、若学校同时购进其中两种不同类型的电脑共50台，请你帮学校设计该如何购买；

(2)、若学校同时购进三种不同类型的电脑共26台（三种类型的电脑都有），并且要求笔记本电脑的购买量不少于15台．

查看试题解析

	甲型	乙型	丙型
价格(元/台)	1000	800	500
销售获利(元/台)	260	190	120