湘教版初中数学七年级下册1.2.1代入消元法同步练习

试卷更新日期：2022-01-16 类型：同步测试

进入出卷网下载

一、单选题

1. 用“代入消元法”解方程组 ${\begin{cases} y = x - 1 ① \\ 2 x - y = 8 ② \end{cases}$ 时，把①代入②正确的是（）

A、2x-x-1=8 B、2x+x-1=8 C、2x+x+1=8 D、2x-x+1=8

查看试题解析
2. 由方程组 ${\begin{array}{l} x + m ＝ 7 \\ y - 1 ＝ m \end{array}$ 可得出x与y的关系式是（）

A、x+y=8 B、x+y=1 C、x+y=-1 D、x+y=-8

查看试题解析
3. 用代入法解方程组 ${\begin{matrix} 2 s + t = 1 ① \\ 3 s - 5 t = 8 ② \end{matrix}$ 下面四个选项中正确的是（　　）

A、由②得 $t = \frac{3 s + 8}{5}$ ，再代入① B、由②得 $s = \frac{8 - 5 t}{3}$ ，再代入① C、由①得 $t = 1 - 2 s$ ，再代入② D、由①得 $s = \frac{1 + t}{2}$ ，再代入②

查看试题解析
4. 两位同学在解方程组时，甲同学由 ${\begin{cases} a x + b y = 2 \\ c x - y = - 4 \end{cases}$ 正确地解出 ${\begin{cases} x = 3 \\ y = - 2 \end{cases}$ ，乙同学因把c写错了，解得 ${\begin{cases} x = -2 \\ y = 2 \end{cases}$ ，则a+b+c的值为（）

A、3 B、0 C、1 D、7

查看试题解析
5. 已知 ${\begin{matrix} 2 x + 3 y = z \\ 3 x + 4 y = 2 z + 6 \end{matrix}$ 且x＋y＝3，则z的值为（）

A、-3 B、-5 C、7 D、1

查看试题解析
6. 已知关于 $x$ ， $y$ 的二元一次方程 $2 x - 3 y = t$ ，其取值如下表，则 $p$ 的值为（）

$x$

$m$

$m + 2$

$y$

$n$

$n - 3$

$t$

5

$p$

A、16 B、17 C、18 D、19

查看试题解析
7. 方程组 ${\begin{array}{l} 2 x + y = ■ \\ x + y = 3 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = ■ \end{array}$ 则被“■”遮盖住的两个数分别为（）

A、5，4 B、5，3 C、1，3 D、5，1

查看试题解析
8. 方程组 ${\begin{array}{l} 2 x + y = \oplus \\ x + y = 3 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = \otimes \end{array}$ ，则 $\oplus$ 和 $\otimes$ 的值分别为（）

A、1，2 B、5，1 C、2，3 D、2，4

查看试题解析

二、填空题

9. 方程组 ${\begin{matrix} x - 3 = 0 \\ x + y = 2 \end{matrix}$ 的解是.

查看试题解析
10. 已知关于 $x ， y$ 的方程组 ${\begin{array}{l} x + 3 y = 4 - a \\ x - y = 3 a \end{array}$ ，给出以下结论：① ${\begin{array}{l} x = 5 \\ y = - 1 \end{array}$ ，是方程组的一个解；②当 $a = - 2$ 时， $x ， y$ 的值互为相反数；③当 $a = 1$ 时，方程组的解也是方程 $x + y = 4 - a$ 的解；④ $x ， y$ 之间的数量关系是 $x - 2 y = 3 ，$ 其中正确的是 (填序号).

查看试题解析
11. 小明在解关于x，y的二元一次方程组 ${\begin{matrix} x + y = Δ \\ 2 x - 3 y = 5 \end{matrix}$ 时，解得 ${\begin{array}{l} x = 4 \\ y = ■ . \end{array}$ 则 $Δ$ 表示的数为.

查看试题解析
12. 若x，y满足方程组 ${\begin{array}{l} x + m = 7 \\ 2 y - 5 = m \end{array}$ 则无论m取何值 $3 x + 6 y - 1 =$ .

查看试题解析
13. 由方程组 ${\begin{matrix} 2 x + m = 1 \\ y - 3 = m \end{matrix}$ 可得出 $x$ 与 $y$ 关系是

查看试题解析
14. 已知关于x，y的二元一次方程2x-3y=t，其部分值如下表所示，则p的值是。

x

m

m+2

y

n

n-2

t

5

p

查看试题解析

三、解答题

15. 已知（3m+2n﹣16）²与|3m﹣n﹣1|互为相反数，求：m+n的值．

查看试题解析
16. 用代入法解方程组 ${\begin{array}{l} 2 x - y = 8 \\ 3 x + 2 y = 3 \end{array}$

查看试题解析
17.
若关于、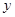的二元一次方程组 ${\begin{matrix} 3 x- 5 y= 2 a \\ 2 x+ 7 y=a- 18 \end{matrix}$ 的解中x与y的值互为相反数，求的值；

查看试题解析
18. 已知关于 $x ， y$ 的方程组 ${\begin{array}{l} x - y = 4 a - 3 \\ x + 2 y = - 5 a \end{array}$ ，

(1)、请用 $a$ 的代数式表示 $y$ ；

(2)、若 $x ， y$ 互为相反数，求 $a$ 的值.

查看试题解析
19. 阅读小强同学数学作业本上的截图内容并完成任务：
解方程组 ${\begin{array}{l} 2 x - y = 3 ① \\ x + y = - 12 ② \end{array}$

解：由①，得 $y = 2 x - 3$ ，③ 第一步

把③代入①，得 $2 x - (2 x - 3) = 3$ .第二步

整理得， $3 = 3$ .第三步

因为 $x$ 可以取任意实数，所以原方程组有无数个解第四步

任务：

(1)、这种解方程组的方法称为；

(2)、利用此方法解方程组的过程中所体现的数学思想是_______；（请你填写正确选项）

A、转化思想 B、函数思想 C、数形结合思想 D、公理化思想

(3)、小强的解法正确吗？（填正确或不正确），如果不正确，请指出错在第步，请选择恰当的解方程组的方法解该方程组.

查看试题解析
20. 善于思考的小明在解方程组 ${\begin{array}{l} 4 x + 10 y = 6 ① \\ 8 x + 22 y = 10 ② \end{array}$ 时，采用了一种“整体代换”的思想.
解法如下：将方程 $8 x + 22 y = 10$ 变形为： $2 (4 x + 10 y) + 2 y = 10$ ③

把方程①代入③得， $2 \times 6 + 2 y = 10$ ，则 $y = - 1$ ；把 $y = - 1$ 代入①得， $x = 4$ ，

所以方程组的解为： ${\begin{array}{l} x = 4 \\ y = - 1 \end{array}$

请你运用“整体代换”的思想解决下列问题：

(1)、解方程组 ${\begin{array}{l} 2 x - 3 y = 7 \\ 6 x - 5 y = 25 \end{array}$ ；

(2)、已知x、y、z满足 ${\begin{array}{l} 3 x - 2 z + 12 y = 47 \\ x + z + 4 y = 19 \end{array}$ ，试求z的值.

查看试题解析
21. 阅读材料：小明在解方程组 ${\begin{matrix} 2 x + 5 y = 3...... ① \\ 4 x + 11 y = 5..... ② \end{matrix}$ 时，采用了一种“整体代换”解法：
解：将方程②变形：4x+10y+y=5即2(2x+5y)+y=5......③

把方程①代入③得：2×3+y=5，

y=-1

y=-1代入①得x=4

∴方程组的解为 ${\begin{matrix} x = 4 \\ y = - 1 \end{matrix}$

请你解决以下问题：

(1)、参考小明的“整体代换”法解方程组 ${\begin{matrix} 3 x - 2 y = 5....... ① \\ 4 x - 4 y = 19..... ② \end{matrix}$

(2)、已知x，y满足方程组： ${\begin{matrix} 3 x^{2} - 2 x y + 12 y^{2} = 47....... ① \\ 2 x^{2} + x y + 8 y^{2} = 36........... ② \end{matrix}$
(i)求 $x^{2} + 4 y^{2}$ 的值；

(ii)求 $\frac{1}{x} + \frac{1}{2 y}$ 的值.

查看试题解析
22. 阅读材料：喜欢看书的刘翔在看一本数学课外读物，发现一种解二元一次方程组的方法叫“整体代换”法：例：解方程组 ${\begin{matrix} 2 x + 3 y = 1 ① \\ 4 x + 7 y = 3 ② \end{matrix}$
解：将方程②变形：4x+6y+y=3，即2（2x+3y）+y=3…③

把方程①代入③得2×1+y=3，

∴y=1．

把y=1代入①得，x=-1，

∴方程组的解为 ${\begin{matrix} x = - 1 \\ y = 1 \end{matrix}$

请你模仿这种方法，解下面方程组：

${\begin{matrix} 3 x - 2 y = 4 \\ 9 x - 5 y = 13 \end{matrix}$ ．

查看试题解析

$x$	$m$	$m + 2$
$y$	$n$	$n - 3$
$t$	5	$p$

x	m	m+2
y	n	n-2
t	5	p