浙教版备考2022年中考数学一轮复习专题37 三角函数及其应用
试卷更新日期:2022-01-15 类型:一轮复习
一、单选题
-
1. 在Rt△ABC中,∠C=90°,AC=4,BC=3,则( )A、sinA= B、cosA= C、cosB= D、tanB=2. 在 中, , , ,则 =( )A、 B、 C、 D、3. 如图,△ABC中,cosB ,sinC ,AC=5,则△ABC的面积是( )
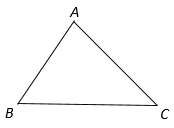 A、 B、12 C、14 D、214. 如图,在▱ABCD中,∠A=60°,AD=2.以点A为圆心,AD为半径作 ,交边AB于点E,G是 的中点,作GF∥BC交CD于点F,以点F为旋转中心,将线段FG按逆时针方向旋转90°至线段FG′,若点G′恰好落在边BC上,则AB的长为( )
A、 B、12 C、14 D、214. 如图,在▱ABCD中,∠A=60°,AD=2.以点A为圆心,AD为半径作 ,交边AB于点E,G是 的中点,作GF∥BC交CD于点F,以点F为旋转中心,将线段FG按逆时针方向旋转90°至线段FG′,若点G′恰好落在边BC上,则AB的长为( ) A、 B、 C、 D、5. 如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,连结CD.若AD=3,AC=2,则cosB的值为( )
A、 B、 C、 D、5. 如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,连结CD.若AD=3,AC=2,则cosB的值为( ) A、 B、 C、 D、6. 图1是一块矩形材料 ,被分割成三块, , ,将三块材料无缝隙不重叠地拼成图2的形状,此时图2恰好是轴对称图形,则
A、 B、 C、 D、6. 图1是一块矩形材料 ,被分割成三块, , ,将三块材料无缝隙不重叠地拼成图2的形状,此时图2恰好是轴对称图形,则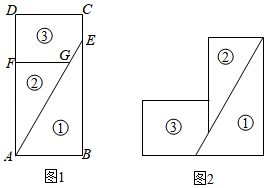 A、 B、 C、 D、7. 如图,在▱ABCD中,AB:AD=3:2,∠ADB=60°,那么cos∠A的值等于( )
A、 B、 C、 D、7. 如图,在▱ABCD中,AB:AD=3:2,∠ADB=60°,那么cos∠A的值等于( ) A、 B、 C、 D、8. 如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB= =( )A、 B、 C、 D、
A、 B、 C、 D、8. 如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB= =( )A、 B、 C、 D、 9. 如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于cosA的是( )
9. 如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于cosA的是( ) A、 B、 C、 D、10. 在△ABC中,∠C=90°,AC= ,AB= ,则cosB的值为( )A、 B、 C、 D、11. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )
A、 B、 C、 D、10. 在△ABC中,∠C=90°,AC= ,AB= ,则cosB的值为( )A、 B、 C、 D、11. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )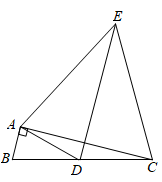 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
12. 在Rt△ABC中,∠C=90°,AC= AB,则tan∠ABC= .13. 如图,⊙O的半径为2,△ABC内接于⊙O,若∠A=60°,∠C=45°,则AC= .
 14. 如图1是超市手推车,如图2是其侧面示意图,已知前后车轮半径均为5cm,两个车轮的圆心的连线AB与地面平行,测得支架AC=BC=60cm,AC、CD所在直线与地面的夹角分别为30°、60°,CD=50cm.
14. 如图1是超市手推车,如图2是其侧面示意图,已知前后车轮半径均为5cm,两个车轮的圆心的连线AB与地面平行,测得支架AC=BC=60cm,AC、CD所在直线与地面的夹角分别为30°、60°,CD=50cm. (1)、求扶手前端D到地面的距离为;(2)、手推车内装有简易宝宝椅,EF为小坐板,打开后,椅子的支点H到点C的距离为10cm,DF=20cm,EF∥AB,∠EHD=45°,坐板EF的宽度为.15. 如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
(1)、求扶手前端D到地面的距离为;(2)、手推车内装有简易宝宝椅,EF为小坐板,打开后,椅子的支点H到点C的距离为10cm,DF=20cm,EF∥AB,∠EHD=45°,坐板EF的宽度为.15. 如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°. (1)、图2中,弓臂两端B1 , C1的距离为cm.(2)、如图3,将弓箭继续拉到点D2 , 使弓臂B2AC2为半圆,则D1D2的长为cm.16. 如图所示,∠AOB=90°,则OA表示的方向是 , 点C在点O的 方向上,要知道点A的位置,除了知道点A的象限角外,还需要知道点A
(1)、图2中,弓臂两端B1 , C1的距离为cm.(2)、如图3,将弓箭继续拉到点D2 , 使弓臂B2AC2为半圆,则D1D2的长为cm.16. 如图所示,∠AOB=90°,则OA表示的方向是 , 点C在点O的 方向上,要知道点A的位置,除了知道点A的象限角外,还需要知道点A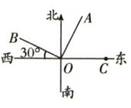 17. 如图,在长和宽分别是8和7矩形内,放置了如图中5个大小相同的正方形,则正方形的边长是.
17. 如图,在长和宽分别是8和7矩形内,放置了如图中5个大小相同的正方形,则正方形的边长是.
三、综合题
-
18. 如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作CE⊥AC交AD的延长线于点E,F为CE的中点,连接DB,DF.
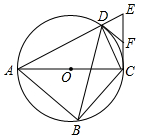 (1)、求∠CDE的度数.(2)、求证:DF是⊙O的切线.(3)、若tan∠ABD=3时,求 的值.19. 如图,根据图中数据完成填空,再按要求答题:
(1)、求∠CDE的度数.(2)、求证:DF是⊙O的切线.(3)、若tan∠ABD=3时,求 的值.19. 如图,根据图中数据完成填空,再按要求答题: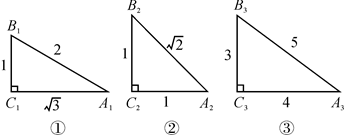 (1)、sin2A1+sin2B1=;sin2A2+sin2B2=;sin2A3+sin2B3=;(2)、观察上述等式,猜想:在Rt△ABC中,∠C=90°.都有:sin2A+sin2B=;(3)、如图,在Rt△ABC中,∠C=90°,∠A , ∠B , ∠C的对边分别是a , b , c;利用三角函数的定义和勾股定理,证明你的猜想;
(1)、sin2A1+sin2B1=;sin2A2+sin2B2=;sin2A3+sin2B3=;(2)、观察上述等式,猜想:在Rt△ABC中,∠C=90°.都有:sin2A+sin2B=;(3)、如图,在Rt△ABC中,∠C=90°,∠A , ∠B , ∠C的对边分别是a , b , c;利用三角函数的定义和勾股定理,证明你的猜想;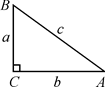 (4)、已知:∠A+∠B=90°,且sinA= , 求sinB.20. 如图,在矩形ABCD中,DE⊥AC于E, ,AB=3,
(4)、已知:∠A+∠B=90°,且sinA= , 求sinB.20. 如图,在矩形ABCD中,DE⊥AC于E, ,AB=3, (1)、求AD的值;(2)、直接写出 的值21. 如图,△ABC中,AB=BC.
(1)、求AD的值;(2)、直接写出 的值21. 如图,△ABC中,AB=BC. (1)、用直尺和圆规作△ABC的中线BD;(不要求写作法,保留作图痕迹);(2)、在(1)的条件下,若BC=6,BD=4,求 的值.22. 在▱ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)、用直尺和圆规作△ABC的中线BD;(不要求写作法,保留作图痕迹);(2)、在(1)的条件下,若BC=6,BD=4,求 的值.22. 在▱ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.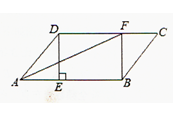 (1)、求证:四边形BFDE是矩形;(2)、若AF平分∠BAD,且AE=3,DE=4,求tan∠BAF的值.23. 如图所示,位于A处的海上救援中心获悉:在其北偏东 方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东 相距20海里的C处救生船,并通知救生船,遇险船在它的正东方向B处,现救生船沿着航线CB前往B处救援,若救生船的速度为20海里/时,请问:
(1)、求证:四边形BFDE是矩形;(2)、若AF平分∠BAD,且AE=3,DE=4,求tan∠BAF的值.23. 如图所示,位于A处的海上救援中心获悉:在其北偏东 方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东 相距20海里的C处救生船,并通知救生船,遇险船在它的正东方向B处,现救生船沿着航线CB前往B处救援,若救生船的速度为20海里/时,请问: (1)、C到AB的最短距离是多少?(2)、救生船到达B处大约需要多长时间?(结果精确到0.1小时:参考数据: , , , , , )24. 如图,某市郊外景区内一条笔直的公路l经过A、B两个景点,景区管委会又开发了风景优美的景点C.经测量,C位于A的北偏东60°的方向上,C位于B的北偏东30°的方向上,且AB=10km.
(1)、C到AB的最短距离是多少?(2)、救生船到达B处大约需要多长时间?(结果精确到0.1小时:参考数据: , , , , , )24. 如图,某市郊外景区内一条笔直的公路l经过A、B两个景点,景区管委会又开发了风景优美的景点C.经测量,C位于A的北偏东60°的方向上,C位于B的北偏东30°的方向上,且AB=10km.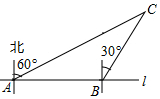 (1)、求景点B与C的距离;(2)、为了方便游客到景点C游玩,景区管委会准备由景点C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)25. 如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2 , ,△ADP沿点A旋转至△ABP’,连接PP’,并延长AP与BC相交于点Q.
(1)、求景点B与C的距离;(2)、为了方便游客到景点C游玩,景区管委会准备由景点C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)25. 如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2 , ,△ADP沿点A旋转至△ABP’,连接PP’,并延长AP与BC相交于点Q. (1)、求证:△APP’是等腰直角三角形;(2)、求∠BPQ的大小;(3)、求CQ的长.26. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE= .
(1)、求证:△APP’是等腰直角三角形;(2)、求∠BPQ的大小;(3)、求CQ的长.26. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE= .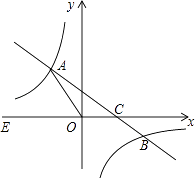 (1)、求该反比例函数和一次函数的解析式;(2)、求△AOC的面积;(3)、直接写出一次函数值大于反比例函数值时自变量x的取值范围.27. 如图, 在 中, , 点 以每秒2个单位长度的速度从点 出发, 沿 方向向终点 匀速运动, 同时点Q以每秒1个単位长度的速度从点 出发, 沿 方向向终点 匀速运动, 连结 . 设运动的时间为 秒.
(1)、求该反比例函数和一次函数的解析式;(2)、求△AOC的面积;(3)、直接写出一次函数值大于反比例函数值时自变量x的取值范围.27. 如图, 在 中, , 点 以每秒2个单位长度的速度从点 出发, 沿 方向向终点 匀速运动, 同时点Q以每秒1个単位长度的速度从点 出发, 沿 方向向终点 匀速运动, 连结 . 设运动的时间为 秒. (1)、求 的长 (用含 的代数式表示).(2)、当 秒时, 求 的面积.(3)、①如图 2,连结 ,当 为直角三角形时,求所有满足条件 的值.
(1)、求 的长 (用含 的代数式表示).(2)、当 秒时, 求 的面积.(3)、①如图 2,连结 ,当 为直角三角形时,求所有满足条件 的值.② 如图3,当点 关于 的对称点 落在直线 上时,求 的值.
28. 如图,在平面直角坐标系中,0为坐标原点,点A、B分别为直线y=- x+6与x轴、y轴的交点.动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的交点分别为C、D,连接CD、QC. (1)、求当t为何值时,点Q与点D重合?(2)、设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;(3)、若⊙P与线段QC只有一个交点,请直接写出t的取值范围.29. 如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F,D.
(1)、求当t为何值时,点Q与点D重合?(2)、设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;(3)、若⊙P与线段QC只有一个交点,请直接写出t的取值范围.29. 如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F,D. (1)、直接写出∠NDE的度数;(2)、如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;(3)、如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD= ,其他条件不变,求线段AM的长.30. 如图,在直角坐标系中,⊙M经过原点O(0,0),点A( ,0)与点B(0,﹣ ),点D在劣弧 上,连接BD交x轴于点C,且∠COD=∠CBO.
(1)、直接写出∠NDE的度数;(2)、如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;(3)、如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD= ,其他条件不变,求线段AM的长.30. 如图,在直角坐标系中,⊙M经过原点O(0,0),点A( ,0)与点B(0,﹣ ),点D在劣弧 上,连接BD交x轴于点C,且∠COD=∠CBO. (1)、求⊙M的半径;(2)、求证:BD平分∠ABO;(3)、在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.
(1)、求⊙M的半径;(2)、求证:BD平分∠ABO;(3)、在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.