浙教版备考2022年中考数学一轮复习专题28 正方形
试卷更新日期：2022-01-15 类型：一轮复习
一、单选题
-
1. 如图，正方形ABCD的边长为3，将长为2 的线段QF的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发，在AB上滑动，同时点F在BC上滑动，当点F到达点C时，运动停止，那么在这个过程中，线段QF的中点M所经过的路线长为（ ）
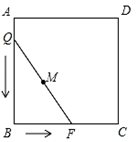A、 B、 C、 D、2. 如图，正方形ABCD的边长是3，BP＝CQ，连接AQ，DP交于点O，并分别与边CD，BC交于点F，E，连接AE，下列结论：①AQ⊥DP；②OA2＝OE•OP；③S△AOD＝S四边形OECF；其中正确结论的个数（ ）
A、1 B、3 C、2 D、03. 如图，在正方形ABCD中放入两个相同小正方形纸片，重叠部分记为①，点E，F的位置如图所示，若D，F，E三点共线，则正方形ABCD与①的面积比为（ ）
A、9+4 B、2 C、3 D、94. 如图，在矩形ABCD中，点E，F，H分别在边AB，BC，AD上，四边形EFGH由两个正方形组成，若BF＝AH＝2，则线段BC的长为（ ）
A、4 B、4.5 C、5 D、5.55. 如图，正方形ABCD的边长为2，E是BC的中点，点P是AC边上的一个动点，连结BP，EP，则BP+EP的最小值为（ ）
A、 B、 C、 D、 +16. 如图，在正方形ABCD中，E是BC的中点，△DEF的面积等于2，则此正方形ABCD的面积等于（ ）
A、6 B、12 C、16 D、207. 如图，Rt△ABC中，∠C＝90°，AC＝3，BC＝4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN，四块阴影部分的面积分别为S1、S2、S3、S4.则S1﹣S2+S3+S4等于（ ）
A、4 B、6 C、8 D、128. 如图所示，点E在正方形ABCD内，满足∠AEB=90° ，AE=6，BE=8，则阴影部分的面积是（ ）
A、48 B、60 C、76 D、80．9. 如图，以直角三角形三边为边向外作三个正方形，若正方形C面积为15，正方形B面积为12，则正方形A的面积为（ ）
A、1 B、2 C、3 D、410. 如图所示，矩形内有两个相邻的正方形，其面积分别为2和8，则图中阴影部分的面积为（ ）
A、 B、2 C、2 D、6二、填空题
-
11. 如图，已知：PA＝2，PB＝4，以AB为边作正方形ABCD，使P、D两点落在直线AB的两侧．当∠APB＝45°时，则PD的长为 ．
12. 如图，在正方形ABCD中，AB=3，点E，F分别在CD，AD上，CE=DF，BE，CF相交于点G．若图中阴影部分的面积与正方形ABCD的面积之比为2：3，则△BCG的周长为 ．
13. 勾股定理有很多种证明方法，我国清代数学家李锐运用下图证明了勾股定理．在Rt△ABC中，已知AB=2BC，分别以AB，BC，AC为边，按如图所示的方式作正方形ABDE，正方形BCFG，正方形ACHI．其中HI与BD交于点N，设四边形ABNI的面积为S1 ， △CHN的面积为S2 ， 则 ．
14. 如图1，直角三角形纸片的一条直角边长为6，剪四块这样的直角三角形纸片，把它们按图2放入一个边长为10 的正方形中(纸片在结合部分不重叠无缝隙)，则图2中阴影部分面积为
15. 如图所示是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A，B，C，D的面积分别为2，5，1，2．则最大的正方形E的面积是
16. 如图所示，点E在正方形．ABCD的边AB上，若EB=1，EC=2，那么正方形ABCD的面积为
17. 如图所示，三个正方形的面积分别为S1=3，S2=2，S3=1，则分别以它们的一边为边围成的三角形中，∠1+∠2=
三、综合题
-
18. 已知，一次函数y=2x+4的图象与x轴、y轴分别交于点A、点B，正方形BOCD的顶点D在第二象限内，直线DE交AB于点E，交x轴于点F，
(1)、求点D的坐标和AB的长；(2)、若△BDE≌△AFE，求点E的坐标；(3)、若点P、点Q是直线BD、直线DF上的一个动点，当△APQ是以AP为直角边的等腰直角三角形时，直接写出Q点的坐标。19. 已知边长为8的正方形 截去一个角后成为五边形 ，点 在线段 上，过点 作 ，垂足为点 ，过点 作 ，垂足为点 ， ， ，设 的长为 ，四边形 的面积记为 .
(1)、求 ， 的长（分别用含 的代数式表示）；(2)、求 关于 的函数关系式，并写出自变量的取值范围；(3)、求四边形 面积的最大值.20. 如图1所示将一块等腰三角板BMN放置与正方形ABCD的∠B重合，连接AN、CM，E是AN的中点，连接BE.
(1)、（观察猜想）CM与BE的位置关系是；CM与BE的数量关系是；
(2)、（探究证明）如图2所示，把三角板BMN绕点B逆时针旋转a（0<a<90），其他条件不变，线段CM与BE的关系是否仍然成立，并说明理由：
(3)、（拓展延伸）若旋转角a=45°，且∠NBE=2∠ABE，求 的值.
21. 如图，点E，F， G，H分别是CD，BC，AB，DA的中点.
(1)、求证：四边形EFGH是平行四边形.(2)、若连接AC，BD， 则当AC，BD满足什么关系时，四边形EFGH是正方形?请说明理由.22. 如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边，上的一点(不与点A，点D重合).将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP，BH.
(1)、求证：∠APB=∠BPH.(2)、当点P在边AD.上移动时，△PDH的周长是否发生变化?请证明你的结论.23. 如图1，这是由8个同样大小的立方体组成的魔方，体积为64.
(1)、求出这个魔方的棱长.(2)、图中阴影部分是一个正方形ABCD，求出阴影部分的面积及其边长.(3)、把正方形ABCD放到数轴上，如图2，使得A与﹣1重合，那么D在数轴上表示的数为.24. 两个长为2 cm，宽为1 cm的矩形，摆放在直线 上(如图①)，CE=2 cm，将矩形ABCD绕着点C顺时针旋转a角，将矩形EFGH绕着点E逆时针旋转相同的角度．
(1)、当旋转到顶点D，H重合时，连接AE，CG，求证：△AED≌△GCD(如图②)；(2)、当a=45°时(如图③)，求证：四边形MHND为正方形．
25. 如图1，在正方形ABCD中，点E，F分别是边BC，AB上的点，且CE=BF．连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC．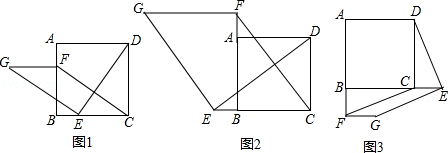
(1)、请判断：FG与CE的数量关系是 ， 位置关系是；(2)、如图2，若点E，F分别是边CB，BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请作出判断并给予证明；(3)、如图3，若点E，F分别是边BC，AB延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断．26. 如图，边长为acm的正方体其上下底面的对角线AC、A1C1与平面H垂直．
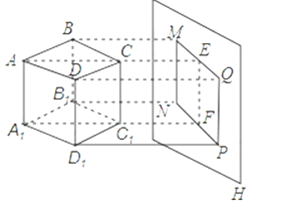(1)、指出正方体六个面在平面H上的正投影图形；(2)、计算投影MNPQ的面积．27. 正在改造的人行道工地上，有两种铺设路面材料：一种是长为acm、宽为bcm的矩形板材（如图1），另一种是边长为ccm的正方形地砖（如图2）．
(1)、用多少块如图2所示的正方形地砖能拼出一个新的正方形？（只要写出一个符合条件的答案即可），并写出新正方形的面积；(2)、现用如图1所示的四块矩形板材铺成一个大矩形（如图3）或大正方形（如图4），中间分别空出一个小矩形和一个小正方形．①试比较中间的小矩形和中间的小正方形的面积哪个大？大多少？
②如图4，已知大正方形的边长比中间小正方形的边长多20cm，面积大3200cm2 ． 如果选用如图2所示的正方形地砖（边长为20cm）铺设图4中间的小正方形部分，那么能否做到不用切割地砖就可直接密铺（缝隙忽略不计）呢？若能，请求出密铺所需地砖的块数；若不能，至少要切割几块如图2的地砖？
28.(1)、如图①，分别以△ABC的边AB、AC为一边向形外作正方形ABDE和正方形ACGF．求证S△AEF＝S△ABC ．
(2)、如图②，分别以△ABC的边AB、AC、BC为边向形外作正方形ABDE、ACGF、BCHI，可得六边形DEFGHI，若S正方形ABDE＝17，S正方形ACGF＝25，S正方形BCHI＝16，求S六边形DEFGHI ．
29. 如图，AB是⊙O的直径，DO⊥AB于点O，连接DA交⊙O于点C，过点C作⊙O的切线交DO于点E，连接BC交DO于点F．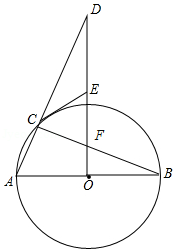
(1)、求证：CE=EF；(2)、连接AF并延长，交⊙O于点G．填空：①当∠D的度数为时，四边形ECFG为菱形；
②当∠D的度数为时，四边形ECOG为正方形．
30. 如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于点D，交AB于点E，点F在DE的延长线上，且AF=CE．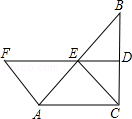
(1)、四边形ACEF是平行四边形吗？说明理由；(2)、当∠B的大小满足什么条件时，四边形ACEF为菱形？请说明你的结论；(3)、四边形ACEF有可能是正方形吗？为什么？