陕西省榆林市2021-2022学年八年级上学期期末数学试卷

试卷更新日期：2022-01-15 类型：期末考试

进入出卷网下载

一、单选题

1. 点 $(- 2 ， - 3)$ 关于x轴对称的点的坐标是（）

A、 $(2 ， 3)$ B、 $(- 2 ， 3)$ C、 $(2 ， - 3)$ D、 $(3 ， 2)$

查看试题解析
2. 以下列各组线段为边作三角形，不能作出直角三角形的是（）

A、1，2， $\sqrt{5}$ B、6，8，10 C、3，7，8 D、0.3，0.4，0.5

查看试题解析
3. 三角板是我们学习数学的工具，一副三角板拼成如图方式，则图中 $∠ 2 - ∠ 1$ 的值为（）

A、30° B、45° C、60° D、不能确定

查看试题解析
4. 用代入消元法解关于x、y的方程组 ${\begin{array}{l} x = 4 y - 3 ， \\ 2 x - 3 y = - 1 \end{array}$ 时，代入正确的是（）

A、 $2 (4 y - 3) - 3 y = - 1$ B、 $4 y - 3 - 3 y = - 1$ C、 $4 y - 3 - 3 y = 1$ D、 $2 (4 y - 3) - 3 y = 1$

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{12} \div 2 = \sqrt{6}$ B、 $\sqrt{2} + \sqrt{2} = 2$ C、 $\sqrt{13} - \sqrt{3} = \sqrt{10}$ D、 $(\sqrt{3} + 1) (\sqrt{3} - 1) = 2$

查看试题解析
6. 班级准备推选一名同学参加学校演讲比赛，在五轮班级预选赛中，甲、乙、丙三名同学五轮预选赛成绩的平均数和方差如下表所示：

甲

乙

丙

平均数/分

96

95

97

方差

0.4

2

2

丁同学五轮预选赛的成绩依次为：97分、96分、98分、97分、97分，根据表中数据，要从甲、乙、丙、丁四名同学中选择一名成绩好又发挥稳定的同学参赛应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 在全国足球联赛中，每场比赛都要分出胜负，已知某足球队连续10场保持不败，共得22分，根据比赛规则：胜一场得3分，平一场得1分，求该足球队胜了多少场？平了多少场？设该足球队胜的场数是x，平的场数是y，根据题意可得方程组为（）

A、 ${\begin{array}{l} x + y = 10 \\ 3 x - y = 22 \end{array}$ B、 ${\begin{array}{l} x + y = 10 \\ 3 x + y = 22 \end{array}$ C、 ${\begin{array}{l} x + y = 10 \\ x + 3 y = 22 \end{array}$ D、 ${\begin{array}{l} x + y = 10 \\ x - 3 y = 22 \end{array}$

查看试题解析
8. 已知直线 $l_{1}$ 交x轴于点 $(- 3 ， 0)$ ，交 $y$ 轴于点 $(0 ， 6)$ ，直线 $l_{2}$ 与直线 $l_{1}$ 关于x轴对称，将直线 $l_{1}$ 向下平移8个单位得到直线 $l_{3}$ ，则直线 $l_{2}$ 与直线 $l_{3}$ 的交点坐标为（）

A、 $(- 1 ， - 4)$ B、 $(- 2 ， - 4)$ C、 $(- 2 ， - 1)$ D、 $(- 1 ， - 1)$

查看试题解析

二、填空题

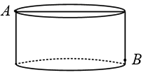
9. 请你写出一个小于﹣1的无理数.

查看试题解析
10. 命题“垂直于同一直线的两条直线互相垂直”是命题.（填“真”或“假”）

查看试题解析
11. 已知在平面直角坐标系中，点 $M (x + 2 y ， x - y)$ 在第一象限，且点M到x轴的距离为2，到y轴的距离为5，则 $2 x + y$ 的值为.

查看试题解析
12. 小红参加学校举办的“我爱我的祖国”主题演讲比赛，她的演讲稿、语言表达、形象风度得分分别为85分，70分，80分，若依次按照40%，30%，30%的百分比确定成绩，则她的平均成绩是分．

查看试题解析
13. 已知 $\sqrt{19}$ 在两个连续的整数a和b之间，则 $a + b$ 的平方根为.

查看试题解析
14. 如图，圆柱形容器高为0.8m，底面周长为4.8m，在容器内壁离底部0.1m的点B处有一只蚊子，此时一只壁虎正好在容器的顶部点A处，若容器壁厚忽略不计，则壁虎捕捉蚊子的最短路程是m.

查看试题解析

三、解答题

15. 计算： $\sqrt{16} + \sqrt[3]{- 64} - \sqrt{3} \times \sqrt{6}$ .

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A D ⊥ B C$ 于点D，点E是 $A D$ 上一点，连接 $B E$ .求证： $∠ B E D > ∠ C$ .

查看试题解析
17. 已知方程组 ${\begin{array}{l} 2 x + y = 6 ， \\ 3 x - y = 4 \end{array}$ 的解也是关于x、y的二元一次方程 $2 a x - 3 y = 0$ 的一组解，求a的值.

查看试题解析
18. 如图，已知 $∠ C + ∠ E = ∠ E A B$ ，求证： $A B // C D$ .

查看试题解析
19. 王亮家距离李刚家6.5千米，星期天王亮骑车去李刚家玩，中途自行车突然“爆胎”，恰好路边有便民服务点，几分钟后车修好了，他加快速度骑车到李刚家.王亮的行驶路程 $s$ （千米）与所用时间 $t$ （分钟）之间的函数图象如图所示：

(1)、求王亮加速后行驶路程s（千米）与所用时间t（分钟）之间的函数关系式；

(2)、求当王亮距离李刚家1.5千米时，t的值.

查看试题解析
20. 某校开展了以“不忘初心，奋斗新时代”为主题的读书活动，校德育处对本校八年级学生九月份“阅读该主题相关书籍的读书量”（下面简称：“读书量”）进行了抽样调查，随机抽取八年级部分学生，对他们的“读书量”（单位：本）进行了统计，并将统计结果绘制成了如下统计图：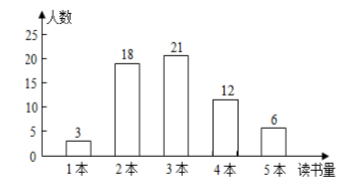

(1)、本次所抽取学生九月份“读书量”的众数为本，中位数为本；

(2)、求本次所抽取学生九月份“读书量”的平均数.

查看试题解析
21. 如图，在平面直角坐标系中，已知 $△ A B C$ 的三个顶点都在网格的格点上.

（1）在图中作出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出点B的对应点 $B_{1}$ 的坐标；
（2）在图中作出 $△ A B C$ 关于y轴对称的 $△ A_{2} B_{2} C_{2}$ ，并写出点B的对应点 $B_{2}$ 的坐标.

查看试题解析
22. 学校计划从某花卉供应商家定制一批花卉来装扮校园（花盆全部为同一型号），该商家委托某货运公司负责这批花卉的运输工作.该货运公司有甲、乙两种专门运输花卉的货车，已知1辆甲型货车和3辆乙型货车满载一次可运输1700盆花卉；2辆甲型货车比3辆乙型货车满载一次少运输200盆花卉.1辆甲型货车满载一次可运输多少盆花卉？1辆乙型货车满载一次可运输多少盆花卉？

查看试题解析
23. 小王与小林进行遥控赛车游戏，终点为点A，小王的赛车从点C出发，以 $4$ 米/秒的速度由西向东行驶，同时小林的赛车从点B出发，以 $3$ 米/秒的速度由南向北行驶（如图）.已知赛车之间的距离小于或等于 $25$ 米时，遥控信号会产生相互干扰， $A C = 40$ 米， $A B = 30$ 米，

(1)、出发 $3$ 秒钟时，遥控信号是否会产生相互干扰？

(2)、当两赛车距A点的距离之和为 $35$ 米时，遥控信号是否会产生相互干扰？

查看试题解析
24. 如图，在平面直角坐标系中，直线 $A B$ 交x轴于点 $A (3 ， 0)$ ，交y轴正半轴于点B，且 $O A = 2 O B$ ，正比例函数 $y = x$ 交直线 $A B$ 于点P， $P M ⊥ x$ 轴于点M， $P N ⊥ y$ 轴于点 $N$ .

(1)、求直线 $A B$ 的函数表达式和点P的坐标；

(2)、在y轴负半轴上是否存在点Q，使得 $△ A P Q$ 为等腰三角形？若存在，求出所有符合条件的点Q的坐标；若不存在，请说明理由.

查看试题解析

	甲	乙	丙
平均数/分	96	95	97
方差	0.4	2	2