河南省平顶山市舞钢市2021-2022学年九年级上学期期末数学试卷
试卷更新日期:2022-01-15 类型:期末考试
一、单选题
-
1. 下列命题中,不正确的是( )A、对角线相等的平行四边形是矩形. B、有一个角为60°的等腰三角形是等边三角形. C、直角三角形斜边上的高等于斜边的一半. D、正方形的两条对角线相等且互相垂直平分.2. 如图①是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图②.关于平移前后几何体的三视图,下列说法正确的是( )
 A、主视图相同 B、左视图相同 C、俯视图相同 D、三种视图都不相同3. 小张同学去展览馆看展览,该展览馆有A、B两个验票口(可进可出),另外还有C、D两个出口(只出不进).则小张从不同的出入口进出的概率是( )A、 B、 C、 D、4. 如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
A、主视图相同 B、左视图相同 C、俯视图相同 D、三种视图都不相同3. 小张同学去展览馆看展览,该展览馆有A、B两个验票口(可进可出),另外还有C、D两个出口(只出不进).则小张从不同的出入口进出的概率是( )A、 B、 C、 D、4. 如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )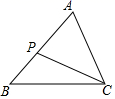 A、 B、 C、 D、5. 在正方形网格中, ABC的位置如图所示,点A、B、C均在格点上,则cosB的值为( )
A、 B、 C、 D、5. 在正方形网格中, ABC的位置如图所示,点A、B、C均在格点上,则cosB的值为( )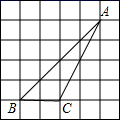 A、 B、 C、 D、6. 甲、乙两地相距60km,则汽车由甲地行驶到乙地所用时间y(小时)与行驶速度x(千米/时)之间的函数图象大致是( )A、
A、 B、 C、 D、6. 甲、乙两地相距60km,则汽车由甲地行驶到乙地所用时间y(小时)与行驶速度x(千米/时)之间的函数图象大致是( )A、 B、
B、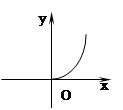 C、
C、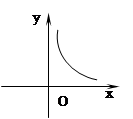 D、
D、 7. 如图,太阳光线与地面成80°角,窗子AB=2米,要在窗子外面上方0.2米的点D处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是( )
7. 如图,太阳光线与地面成80°角,窗子AB=2米,要在窗子外面上方0.2米的点D处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是( ) A、 米 B、 米 C、 米 D、 米8. 如图,反比例函数y= (x<0)与一次函数y=x+4的图象交于A、B两点的横坐标分别为-3,-1.则关于x的不等式 <x+4(x<0)的解集为( )
A、 米 B、 米 C、 米 D、 米8. 如图,反比例函数y= (x<0)与一次函数y=x+4的图象交于A、B两点的横坐标分别为-3,-1.则关于x的不等式 <x+4(x<0)的解集为( )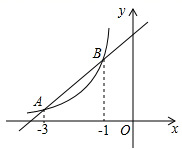 A、x<-3 B、-3<x<-1 C、-1<x<0 D、x<-3或-1<x<09. 某钢铁厂一月份生产钢铁560吨,从二月份起,由于改进操作技术,使得第一季度共生产钢铁1850吨,问二、三月份平均每月的增长率是多少?若设二、三月份平均每月的增长率为x,则可得方程( )A、 B、 C、 D、10. 如图在△ABC外任取一点O,连接AO、BO、CO,并取它们的中点D、E、F,得到△DEF,则下列说法正确的个数是( )
A、x<-3 B、-3<x<-1 C、-1<x<0 D、x<-3或-1<x<09. 某钢铁厂一月份生产钢铁560吨,从二月份起,由于改进操作技术,使得第一季度共生产钢铁1850吨,问二、三月份平均每月的增长率是多少?若设二、三月份平均每月的增长率为x,则可得方程( )A、 B、 C、 D、10. 如图在△ABC外任取一点O,连接AO、BO、CO,并取它们的中点D、E、F,得到△DEF,则下列说法正确的个数是( )①△ ABC与 △DEF是位似图形;② △ABC与△DEF是相似图形;③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
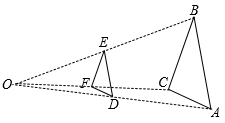 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若反比例函数y= 的图象经过点(﹣3,4),则此函数在每一个象限内y随x的增大而.12. 设a,b是方程x2+x﹣2021=0的两个实数根,则a2+2a+b的值为.13. 如图,小明周末晚上陪父母在锦江绿道上散步,他由灯下A处前进4米到达B处时,测得影子BC长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子DE长为米.
 14. 如图,已知Rt ABC中,斜边BC上的高AD=4,cosB ,则AC=.
14. 如图,已知Rt ABC中,斜边BC上的高AD=4,cosB ,则AC=.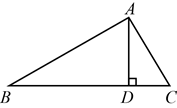 15. 双曲线y1、y2在第一象限的图象如图所示,y2 ,过y1上的任意一点A作x轴的平行线交y2于点B,交y轴于点C,如果 =2,那么y1的函数表达式是 .
15. 双曲线y1、y2在第一象限的图象如图所示,y2 ,过y1上的任意一点A作x轴的平行线交y2于点B,交y轴于点C,如果 =2,那么y1的函数表达式是 .
三、解答题
-
16.(1)、计算: tan45°+3tan30°•cos60°.(2)、解方程:(x﹣2)(x﹣5)=﹣2.17. 小明和小刚用如图所示的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,当两个转盘所转到的数字之积为奇数时,小明得2分;当所转到的数字之积为偶数时,小刚得1分.这个游戏对双方公平吗?若公平,说明理由.若不公平,如何修改规则才能使游戏对双方公平?
 18. 如图
18. 如图 (1)、如图1所示,快下降到地面的某伞兵在灯光下的影子为AB.试确定灯源P的位置,并画出竖立在地面上木桩的影子EF.(保留作图痕迹,不要求写作法)(2)、画出图2实物的三视图.19. 深圳市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点D处,操控者站在点A处,无人机测得点A的俯角为30°,测得教学楼楼顶点C处的俯角为45°,又经过人工测量得到操控者和教学楼BC的距离为57米,求教学楼BC的高度.( ≈1.7)
(1)、如图1所示,快下降到地面的某伞兵在灯光下的影子为AB.试确定灯源P的位置,并画出竖立在地面上木桩的影子EF.(保留作图痕迹,不要求写作法)(2)、画出图2实物的三视图.19. 深圳市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点D处,操控者站在点A处,无人机测得点A的俯角为30°,测得教学楼楼顶点C处的俯角为45°,又经过人工测量得到操控者和教学楼BC的距离为57米,求教学楼BC的高度.( ≈1.7) 20. 如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.
20. 如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG. (1)、求证:四边形DEFG为菱形;
(1)、求证:四边形DEFG为菱形;
(2)、若CD=8,CF=4,求 的值.21. 通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣微增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x≤10和10<x<20时,图象是线段;当20≤x≤45时,图象是反比例函数的一部分,其中BC AD x轴. (1)、求点A对应的指标值;(2)、张老师在一节课上讲解一道数学综合题需要18分钟,他能否确保学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.22. 如图, ,DB平分∠ADC,过点B作 交AD于M.连接CM交DB于N.
(1)、求点A对应的指标值;(2)、张老师在一节课上讲解一道数学综合题需要18分钟,他能否确保学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.22. 如图, ,DB平分∠ADC,过点B作 交AD于M.连接CM交DB于N.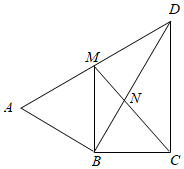 (1)、求证: ;(2)、若 ,求MN的长.23. 模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)、求证: ;(2)、若 ,求MN的长.23. 模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下: (1)、建立函数模型
(1)、建立函数模型设矩形相邻两边的长分别为x,y,由矩形的面积为4,得 ,即 ;由周长为m,得 ,即 .满足要求的 应是两个函数图象在第象限内交点的坐标.
(2)、画出函数图象函数 的图象如图所示,而函数 的图象可由直线 平移得到.请在同一直角坐标系中直接画出直线 .
(3)、平移直线 ,观察函数图象①当直线平移到与函数 的图象有唯一交点 时,周长m的值为 ▲ ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)、得出结论若能生产出面积为4的矩形模具,则周长m的取值范围为.