甘肃省酒泉市金塔县2021-2022学年九年级上学期期末考试数学试卷

试卷更新日期：2022-01-15 类型：期末考试

进入出卷网下载

一、单选题

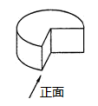
1. 下列方程中是关于x的一元二次方程的是（）

A、x²+ $\frac{1}{x}$ =0 B、ax²+bx+c=0 C、(x-1)(x+2)=1 D、3x-2xy-5y²=0

查看试题解析
2. 如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 已知 $C$ 是 $A B$ 的黄金分割点（ $A C < B C$ ），若 $A B = 4 cm$ ，则BC的长为（）

A、（ $2 \sqrt{5} - 2$ ） $cm$ B、（ $6 - 2 \sqrt{5}$ ） $cm$ C、（ $\sqrt{5} - 1$ ） $cm$ D、（ $3 - \sqrt{5}$ ） $cm$

查看试题解析
4. 用配方法解一元二次方程 $2 x^{2} - 4 x = 1$ ，配方后的结果是（）

A、 ${(x - 1)}^{2} = \frac{3}{2}$ B、 ${(2 x - 1)}^{2} = 0$ C、 $2 {(x - 1)}^{2} = 1$ D、 ${(x + 2)}^{2} = \frac{3}{2}$

查看试题解析
5. 矩形具有而菱形不具有的性质是（　　）

A、对角线相等 B、对角线平分一组对角 C、对角线互相平分 D、对角线互相垂直

查看试题解析
6. 若点 $A (- 5 ， y_{1}) ， B (1 ， y_{2}) ， C (5 ， y_{3})$ 都在反比例函数 $y = - \frac{5}{x}$ 的图象上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{3} < y_{1}$ C、 $y_{1} < y_{3} < y_{2}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
7. 李明参加的社区抗疫志愿服务团队共有A、B、C、D四个服务项目，其中每个服务项目又分为第一小组和第二小组，则李明分到A项目的第一小组的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{3}{8}$

查看试题解析
8. 如图，一块矩形ABCD绸布的长AB=a，宽AD=1，按照图中的方式将它裁成相同的三面矩形彩旗，如果裁出的每面彩旗与矩形ABCD绸布相似，则a的值等于（）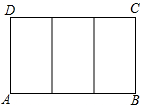

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

查看试题解析
9. 如图，四边形ABCD是菱形，AC＝8，tan∠DAC＝ $\frac{3}{4}$ ，DH⊥AB于H，则点D到AB边距离等于（）

A、4 B、5 C、 $\frac{24}{5}$ D、 $\frac{12}{5}$

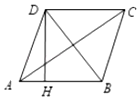查看试题解析
10. 某小区A楼居民今年从三月开始到五月底全部接种新冠疫苗．已知该楼常驻人口285人，三月已有60人接种新冠疫苗，四月、五月实现接种人数较前一个月的平均增长率为x，则下面所列方程正确的是（）

A、60（1＋x）²＝285 B、60（1﹣x）²＝285 C、60（1＋x）＋60（1＋x）²＝285 D、60＋60（1＋x）＋60（1＋x）²＝285

查看试题解析

二、填空题

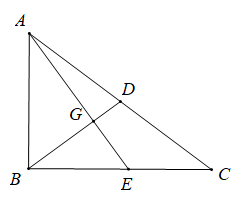
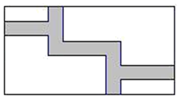
11. 方程x（x﹣3）=x﹣3的根是．

查看试题解析
12. 若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点A(-2，4)和点B(8，a)，则a的值为.

查看试题解析
13. 在 $△ A B C$ 中， $D E ∥ B C$ ， $D E$ 分别交 $A B$ 、 $A C$ 于点 $D$ 、 $E$ ，已知 $A B = 6$ ， $A D = 2$ ， $E C = 3$ ，则 $A E =$ .

查看试题解析
14. 计算： $\sqrt{\frac{1}{3}}$ × $\sqrt{6}$ ﹣sin45°＝.

查看试题解析
15. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $c o s A = \frac{1}{2}$ ，则 $∠ B =$ ．

查看试题解析
16. 在-1，3，5，7中随机选取一个数记为 $a$ ，再从余下的数中随机取一个数记为 $b$ ，则一次函数 $y = a x + b$ 经过一、三、四象限的概率为.

查看试题解析
17. 如图，在长为20m，宽为12m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪，要使草坪的面积为整个矩形面积的 $\frac{3}{4}$ ，如果设道路的宽为x m，则根据题意可列出方程．

查看试题解析
18. 在 $△ A B C$ 和 $△ D E F$ 中， $∠ A = ∠ D = 105 °$ ， $A C = 4 c m$ ， $A B = 6 c m$ ， $D E = 3 c m$ ，则 $D F =$ 时， $△ A B C$ 和 $△ D E F$ 相似．

查看试题解析
19. 若一个三角形的三边长均满足方程x²﹣6x+8=0，则此三角形的周长为．

查看试题解析
20. 下列各图中的三个数之间具有相同规律，依此规律用含m，n的代数式表示y，则y=.

查看试题解析

三、解答题

21. 6tan²30°﹣sin60°﹣2tan45°

查看试题解析
22. 解方程： $(3 x + 2) (x + 3) = x + 14$

查看试题解析
23. 如图所示，图中的小方格都是边长为1的正方形， $△ A B C$ 与 $Δ A^{'} B^{'} C^{'}$ 是以点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上.

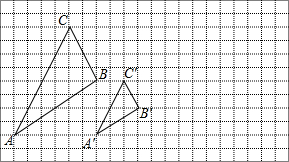
⑴画出位似中心点O；

⑵直接写出 $△ A B C$ 与 $△ A' B' C'$ 的位似比；

⑶以位似中心O为坐标原点，以格线所在直线为坐标轴建立平面直角坐标系，画出△A'B'C'关于点O中心对称的△A″B″C″，并直接写出 △A″B″C″ 各顶点的坐标.

查看试题解析
24. 在一次试验中，每个电子元件的状态有两种可能：在一定时间段内电流可正常通过的状态即“通电”状态；在一定时间段内电流无法通过的状态即“断开”状态，并且这两种状态的可能性相等.如图，请完成下面问题：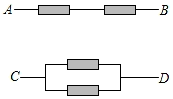

(1)、在一定时间段内，A、B之间电流能够正常通过的概率为；

(2)、用树状图或表格计算在一定时间段内C、D之间电流能够正常通过的概率.

查看试题解析
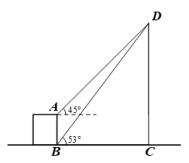25. 如图，从楼层底部 $B$ 处测得旗杆 $C D$ 的顶端 $D$ 处的仰角是 $53 °$ ，从楼层顶部 $A$ 处测得旗杆 $C D$ 的顶端 $D$ 处的仰角是 $45 °$ ，已知楼层 $A B$ 的楼高为 $3$ 米.求旗杆 $C D$ 的高度约为多少米?（参考数据： $\sin 53 ° \approx \frac{4}{5} ， \cos 53 ° \approx \frac{3}{5} ， \tan 53 ° \approx \frac{4}{3}$ ）

查看试题解析
26. 已知：如图，▱ABCD中，AC=BC，M、N分别是AB和CD的中点，求证：四边形AMCN是矩形.

查看试题解析
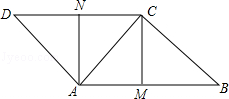27. 如图，一次函数y＝kx+b的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于点A（1，4）、B（4，n）.

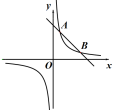(1)、求这两个函数的表达式；

(2)、请结合图象直接写出不等式 $k x + b \leq \frac{m}{x}$ 的解集；

(3)、连接OA，OB，求△OAB的面积.

查看试题解析
28. 某果园有100棵桃树，一棵桃树平均结1000个桃子，现准备多种一些桃树以提高产量，试验发现，每多种一棵桃树，每棵树的产量就会减少2个，但多种的桃树不能超过100棵，如果要使产量增加15.2%，那么应多种多少棵桃树？

查看试题解析
29. 如图，在Rt△ABC中，∠ABC＝90°，点D是斜边AC的中点，连接DB，线段AE⊥线段BD交BC于点E交DB于点G，垂足为点G．

(1)、求证：EB²＝EG•EA；

(2)、联结CG，若∠CGE＝∠DBC．求证：BE＝CE．

查看试题解析