四川省达州市通川区2021-2022学年九年级上学期期末数学试卷
试卷更新日期:2022-01-15 类型:期末考试
一、单选题
-
1. 矩形具有而菱形不具有的性质是( )
A、两组对边分别平行 B、对角线相等 C、对角线互相平分 D、两组对角分别相等2. 把方程化成(a,b为常数)的形式,a,b的值分别是( )A、2,7 B、2,5 C、 , 7 D、 , 53. 若 , 则的值为( ).A、 B、 C、 D、4. 如图所示的几何体,其左视图是( ).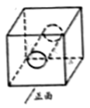 A、
A、 B、
B、 C、
C、 D、
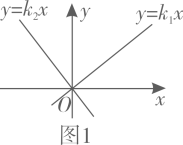
D、 5. 已知 , 则函数的图象大致是( )A、
5. 已知 , 则函数的图象大致是( )A、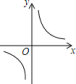 B、
B、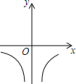 C、
C、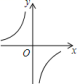 D、
D、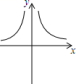 6. 问题:已知方程 , 求一个一元二次方程,使它的根分别是已知方程根的一半.
6. 问题:已知方程 , 求一个一元二次方程,使它的根分别是已知方程根的一半.解:设所求方程的根为 , 则 , 所以.把代入已知方程,得 , 化简,得所求方程为.这种利用方程根的代换求新方程的方法,我们称为“换根法”.
应用:已知方程 , 求一个关于的一元二次方程,使它的根是已知方程根的相反数,则所求方程为( )
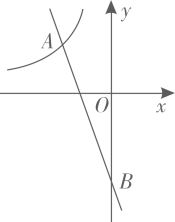
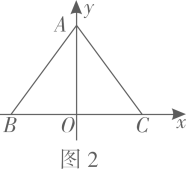
A、 B、 C、 D、7. 对于反比例函数 , ①这个函数图象的两个分支分别位于第二、四象限,②这个函数的图象既是轴对称图形又是中心对称图形,③点不在这个函数图象上,④若点和点在该函数图象上,则.上述四个判断中,不正确的个数是( )A、3 B、2 C、1 D、08. 如图,身高1.5米的小明(AB)在太阳光下的影子AG长1.8米,此时,立柱CD的影子一部分是落在地面的CE,一部分是落在墙EF上的EH.若量得米,米,则立柱CD的高为( ).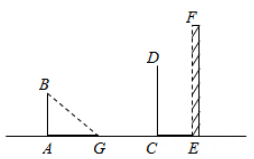 A、2.5m B、2.7m C、3m D、3.6m9. 如图,函数的图象经过斜边OB的中点C,连结AC.如果 , 那么的周长为( ).
A、2.5m B、2.7m C、3m D、3.6m9. 如图,函数的图象经过斜边OB的中点C,连结AC.如果 , 那么的周长为( ).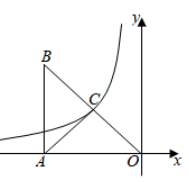 A、 B、 C、 D、10. 如图,已知四边形ABCD是矩形,点E在BA的延长线上, , EC分别交AD,BD于点F,G,若 , 则的值为( ).
A、 B、 C、 D、10. 如图,已知四边形ABCD是矩形,点E在BA的延长线上, , EC分别交AD,BD于点F,G,若 , 则的值为( ).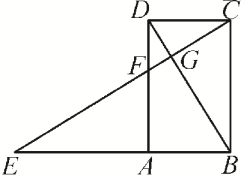 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
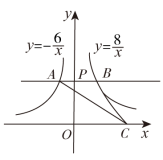
11. 计算: .12. 在不透明的口袋里装有4个黑色棋子和若干白色棋子,每个棋子除颜色外完全相同.从口袋里随机摸出一个棋子,摸到黑球的概率是 , 则白色棋子个数为.13. 如图,过轴正半轴上的任意一点 , 作轴的平行线,分别与反比例函数和的图象交于点和点 , 若点是轴上任意一点,连接 , , 则的面积为.
 14. 如图,有一块长宽的矩形空地,计划在这块空地上修建两块相同的矩形绿地,两块绿地之间及周边留有宽度相同的人行通道,两块绿地的面积和为.设人行通道的宽度为 , 根据题意可列方程:.
14. 如图,有一块长宽的矩形空地,计划在这块空地上修建两块相同的矩形绿地,两块绿地之间及周边留有宽度相同的人行通道,两块绿地的面积和为.设人行通道的宽度为 , 根据题意可列方程:. 15. 如图,在正方形ABCD中,对角线相交于点是OB的中点,连接AE并延长交BC于点若的面积为1,则正方形ABCD的面积为.
15. 如图,在正方形ABCD中,对角线相交于点是OB的中点,连接AE并延长交BC于点若的面积为1,则正方形ABCD的面积为.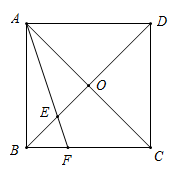 16. 如图1,动点从菱形ABCD的顶点出发,沿以的速度运动到点D停止.设点的运动时间为的面积为.表示与的函数关系的图象如图2所示,则的值为.
16. 如图1,动点从菱形ABCD的顶点出发,沿以的速度运动到点D停止.设点的运动时间为的面积为.表示与的函数关系的图象如图2所示,则的值为.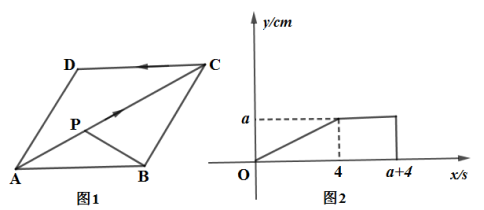
三、解答题
-
17. 已知:关于x的方程.(1)、不解方程:判断方程根的情况;(2)、若方程有一个根为1,求m的值.18. 如图,A型、B型、C型三张矩形卡片的边长如图所示,将三张矩形卡片分别放入三个信封中,三个信封的外表完全相同;
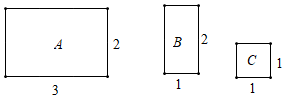 (1)、从这三个信封中随机抽取1个信封,则抽中A型矩形的概率为;(2)、先从这三个信封中随机抽取1个信封(不放回),再从余下的两个信封中随机抽取1个信封,求事件“两次抽中的矩形卡片能拼成(无重叠无缝隙)一个新矩形”发生的概率.(列表法或树状图)19. 一个几何体的三种视图如图所示,
(1)、从这三个信封中随机抽取1个信封,则抽中A型矩形的概率为;(2)、先从这三个信封中随机抽取1个信封(不放回),再从余下的两个信封中随机抽取1个信封,求事件“两次抽中的矩形卡片能拼成(无重叠无缝隙)一个新矩形”发生的概率.(列表法或树状图)19. 一个几何体的三种视图如图所示,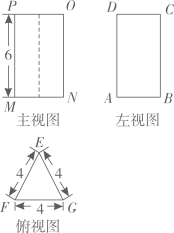
 (1)、这个几何体的名称是 , 其侧面积为;(2)、在右面方格图中画出它的一种表面展开图;(3)、求出左视图中AB的长.20. 某商店进了一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,使库存减少最快,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天多售出2件,当每件衬衫降价多少元时,商场平均每天盈利达到1200元?21. 如图1是一台手机支架,图2是其侧面示意图,AB,BC可分别绕点A,B转动,测量知 , .当AB,BC转动到 , 时,求点C到AE的距离.(结果保留小数点后一位,参考数据: , )
(1)、这个几何体的名称是 , 其侧面积为;(2)、在右面方格图中画出它的一种表面展开图;(3)、求出左视图中AB的长.20. 某商店进了一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,使库存减少最快,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天多售出2件,当每件衬衫降价多少元时,商场平均每天盈利达到1200元?21. 如图1是一台手机支架,图2是其侧面示意图,AB,BC可分别绕点A,B转动,测量知 , .当AB,BC转动到 , 时,求点C到AE的距离.(结果保留小数点后一位,参考数据: , )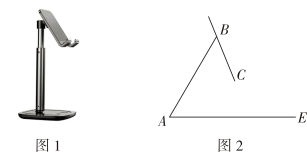 22. 在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:
22. 在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:如图,将矩形ABCD的四边BA,CB,DC,AD分别延长至E,F,G,H,使得 , BF=DH,连接EF,FG,GH,HE.
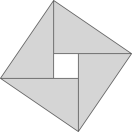
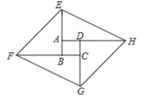 (1)、判断四边形EFGH的形状,并证明;(2)、若矩形ABCD是边长为1的正方形,且 , , 求AE的长.23. 心理学家研究发现,一般情况下,一节课40分钟,学生的注意力随教师讲课时间的变化而变化.学生的注意力指数y随时间x(分)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)、判断四边形EFGH的形状,并证明;(2)、若矩形ABCD是边长为1的正方形,且 , , 求AE的长.23. 心理学家研究发现,一般情况下,一节课40分钟,学生的注意力随教师讲课时间的变化而变化.学生的注意力指数y随时间x(分)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分). (1)、分别求出线段AB和双曲线CD的函数关系式.(2)、上课后的第5分钟与第30分钟相比较,分钟时学生的注意力更集中.(3)、一道数学题,需要讲18分钟,为了学生听课效果较好,要求学生的注意力指数不低于40,那么经过适当的时间安排,教师能否在学生注意力达到所需状态下讲完这道题?
(1)、分别求出线段AB和双曲线CD的函数关系式.(2)、上课后的第5分钟与第30分钟相比较,分钟时学生的注意力更集中.(3)、一道数学题,需要讲18分钟,为了学生听课效果较好,要求学生的注意力指数不低于40,那么经过适当的时间安排,教师能否在学生注意力达到所需状态下讲完这道题?