河南省南阳市南召县2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-01-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列命题中，不正确的是（）

A、对角线相等的平行四边形是矩形． B、有一个角为60°的等腰三角形是等边三角形． C、直角三角形斜边上的高等于斜边的一半． D、正方形的两条对角线相等且互相垂直平分．

查看试题解析
2. 不透明的袋子里共装有4个黑球和6个白球，这些球除了颜色不同外，其余都完全相同，随机从袋子中摸出一个球，摸到黑球的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{6}$ C、 $\frac{2}{3}$ D、 $\frac{2}{5}$

查看试题解析
3. 下列函数是 $y$ 关于 $x$ 的反比例函数的是（）

A、 $y = \frac{1}{x - 1}$ B、 $y = \frac{1}{x^{3}}$ C、 $y = - \frac{3}{x}$ D、 $y = - \frac{x}{4}$

查看试题解析
4. 如图，在△ABC中，DE∥BC，S_△ADE＝S_梯形_DBCE ，则DE：BC为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
5. 某商品经过连续两次降价，售价由原来的每件25元降到每件16元，则平均每次降价的百分率为（）.

A、 $20 %$ B、 $40 %$ C、 $18 %$ D、 $36 %$

查看试题解析
6. 初三(1)班周沫同学拿了A，B，C，D四把钥匙去开教室前、后门的锁，其中A钥匙只能开前门，B钥匙只能开后门，任意取出一把钥匙能够一次打开教室门的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、1 D、 $\frac{1}{4}$

查看试题解析
7. 如图，在菱形ABCD中，DE⊥AB， $\cos A = \frac{3}{5}$ ，BE＝2，则tan∠DBE的值是（　　）

A、 $\frac{1}{2}$ B、2 C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
8. 已知 $(- 3 ， y_{1})$ ， $(1 ， y_{2})$ ， $(5 ， y_{3})$ ，是抛物线 $y = - 2 x^{2} - 4 x + m$ 上的点，则（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{2} > y_{1} > y_{3}$ C、 $y_{1} = y_{2} > y_{3}$ D、 $y_{1} > y_{2} = y_{3}$

查看试题解析
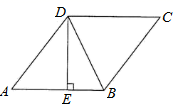9. 某商店今年10月份的销售额是2万元，12月份的销售额是2.88万元，从10月份到12月份，该商店销售额平均每月的增长率为（）

A、44% B、22% C、20% D、10%

查看试题解析
10. 如图是抛物线 $y = - (x + 1)^{2} + k$ 的部分图象，其顶点为M，与y轴交于点（0，3），与x轴的一个交点为A，连接MO，MA.以下结论：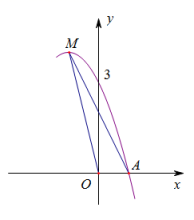
①常数 $k = 3$ ；②抛物线经过点（－2，3）；③ $S_{△ O M A} = 4$ ；④当 $x = - 3 + \frac{2019}{2020}$ 时， $y > 0$ .
其中正确的是（）

A、①③ B、②③ C、②④ D、①④

查看试题解析

二、填空题

11. 一元二次方程x（x﹣3）=3﹣x的根是.

查看试题解析
12. 设a，b是方程x²＋x﹣2021＝0的两个实数根，则a²＋2a＋b的值为.

查看试题解析
13. 如图所示，某商场要在一楼和二楼之间搭建扶梯 $B C$ ，已知一楼与二楼之间的地面高度差为 $3.5$ 米，扶梯 $B C$ 的坡度 $i = \sqrt{3} ： 3$ ，则扶梯 $B C$ 的长度为米.

查看试题解析
14. 如图，四边形ABCD是矩形，AB＝2，AD＝ $\sqrt{2}$ ，以点A为圆心，AB长为半径画弧，交CD于点E，交AD的延长线于点F，则图中阴影部分的面积是．

查看试题解析
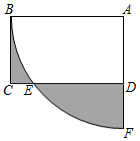15. 如图，在三角形ABC中，∠BAC＝90°，AC＝12，AB＝10，D是AC上一动点，以AD为直径的⊙O交BD于点E，则线段CE的最小值是.

查看试题解析

三、解答题

16. 已知x＝1是一元二次方程（a﹣2）x²+（a²﹣3）x﹣a+1＝0的一个根，求a的值.

查看试题解析
17. 已知：x，y为实数，且 $y < \sqrt{x - 1} + \sqrt{1 - x} + 3$ ，化简： $| y - 3 | - \sqrt{y^{2} - 8 y + 16}$ ．

查看试题解析
18. 已知关于x的方程ax²+（a﹣3）x﹣3＝0（a≠0）.

(1)、求证：方程总有两个实数根；

(2)、若方程有两个不相等的负整数根，求整数a的值.

查看试题解析
19. 如图，AB＝AC，CA平分∠BCD，E点在BC上，且∠BAE＝∠CAD＝90°，求证：CD＝BE.

查看试题解析
20. 如图，在 $R t Δ A B C$ 中， $∠ B A C = 90 °$ ， $∠ C = 30 °$ ，以边 $A C$ 上一点 $O$ 为圆心， $O A$ 为半径作 $⊙ O$ ， $⊙ O$ 恰好经过边 $B C$ 的中点 $D$ ，并与边 $A C$ 相交于另一点 $F$ .

(1)、求证： $B D$ 是 $⊙ O$ 的切线.

(2)、若 $A B = \sqrt{3}$ ， $E$ 是半圆 $\overset{⌢}{A G F}$ 上一动点，连接 $A E$ ， $A D$ ， $D E$ .填空：
①当 $\overset{⌢}{A E}$ 的长度是时，四边形 $A B D E$ 是菱形；

②当 $\overset{⌢}{A E}$ 的长度是时， $Δ A D E$ 是直角三角形.

查看试题解析
21. 在 $R t △ A B C$ 中与 $R t △ D C E$ 中， $∠ A C B = ∠ D C E = 90 ° ， ∠ B A C = ∠ D E C = 30 °$ ， $A C = D C = \sqrt{3}$ ，将 $R t △ D C E$ 绕点 $C$ 顺时针旋转，连接 $B D ， A E$ ，点 $F ， G$ 分别是 $B D ， A E$ 的中点，连接 $C F ， C G$ .

(1)、观察猜想
如图1，当点 $D$ 与点 $A$ 重合时， $C F$ 与 $C G$ 的数量关系是，位置关系是；

(2)、类比探究
当点 $D$ 与点 $A$ 不重合时，（1）中的结论是否成立？如果成立，请仅就图2的情形给出证明；如果不成立，请说明理由.

(3)、问题解决
在 $R t △ D C E$ 旋转过程中，请直接写出 $△ C F G$ 的面积的最大值与最小值.

查看试题解析
22. 如图，已知反比例函数y₁＝ $\frac{k}{x}$ 的图象与一次函数y₂＝x+b的图象交于点A（1，4），点B（﹣4，n）.

(1)、求反比例函数和一次函数的表达式；

(2)、求△OAB的面积；

(3)、直接写出y₂＞y₁时自变量x的取值范围.

查看试题解析
23. 问题探究

(1)、如图1，AB是半圆O的直径，AB＝8.P是 $\overset{⌢}{A B}$ 上一点，且 $\overset{⌢}{P B}$ ＝2 $\overset{⌢}{P A}$ ，连接AP，BP.∠APB的平分线交AB于点C，过点C分别作CE⊥AP、CF⊥BP，垂足分别为E、F.求线段CF的长.

(2)、问题解决
如图2，是某公园内“青少年活动中心”的设计示意图.已知⊙O的直径AB＝70m，点C在⊙O上，且CA＝CB.在AB上任取一点P，连接CP并延长，交⊙O于点D，连接AD、BD.过点P分别作PE⊥AD、PF⊥BD，垂足分别为E、F.按设计要求，四边形PEDF内部为室内活动区，阴影部分是户外活动区，圆内其余部分为绿化区.设AP的长为x（m），阴影部分的面积为y（m²）.
①求y与x之间的函数关系式；

②按照“青少年活动中心”的设计要求，发现当AP的长度为30m时，整体布局比较合理.当AP＝30m时，试求室内活动区（四边形PEDF）的面积.

查看试题解析