贵州省黔西南布依族苗族自治州2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-01-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，y是关于x的二次函数的是（）

A、y＝4x+2 B、y＝（x﹣1）²﹣x² C、y＝3x²+5﹣4x D、y $= \frac{1}{x^{2}}$

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若x＝1是方程x²﹣ax﹣1＝0的一个根，则实数a＝（）

A、0 B、﹣1 C、1 D、2

查看试题解析
4. 下列成语描述的事件为随机事件的是（）

A、偷天换日 B、水涨船高 C、守株待兔 D、旭日东升

查看试题解析
5. 若 $(1 - m) x^{m^{2} + 1} + 3 m x - 2 = 0$ 是关于x的一元二次方程，则该方程的一次项系数是（）

A、﹣1 B、±1 C、﹣3 D、±3

查看试题解析
6. △ABC在平面直角坐标系中的位置如图所示，将其绕点P顺时针旋转得到△A'B'C′，则点P的坐标是（）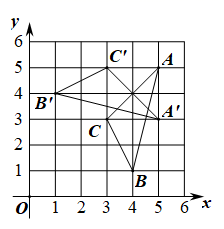

A、（4，5） B、（4，4） C、（3，5） D、（3，4）

查看试题解析
7. 在同一直角坐标系中，一次函数 $y = a x + b$ 与二次函数 $y = b x^{2} + a$ 的大致图象可以是（）

A、 B、 C、 D、

查看试题解析
8. 如图，四边形 $A B C D$ 是半径为2的 $⊙ O$ 的内接四边形，连接 $O A ， O C$ .若 $∠ A O C ： ∠ A B C = 4 ： 3$ ，则 $\overset{⌢}{A C}$ 的长为（）

A、 $\frac{3}{5} π$ B、 $\frac{4}{5} π$ C、 $\frac{6}{5} π$ D、 $\frac{8}{5} π$

查看试题解析
9. 已知关于x的方程x²﹣2（a﹣1）x+a²﹣a﹣2＝0有两个不相等的实数根x₁ ， x₂ ，且x₁ ， x₂满足 $x_{1}^{2} + x_{2}^{2} - x_{1} x_{2} = 16$ ，则a的值为（）

A、6 B、﹣1 C、6或﹣1 D、1或﹣6

查看试题解析
10. 若随意向如图所示的正方形内抛一粒石子，则石子落在阴影部分的概率是（）

A、 $\frac{π}{2} -$ 1 B、1 $- \frac{π}{4}$ C、 $\frac{π}{2}$ D、1

查看试题解析
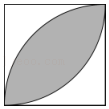11. 如图，⊙O的半径为2 $\sqrt{3}$ ， PA，PB，CD分别切⊙O于点A，B，E，CD分别交PA，PB于点C，D，且P，E，O三点共线.若∠P＝60°，则CD的长为（）

A、4 B、2 $\sqrt{3}$ C、3 $\sqrt{3}$ D、6

查看试题解析
12. 二次函数y＝ax²+bx+c（a，b，c是常数，a≠0）的自变量x与函数值y的部分对应值如表：
x
…
﹣2
﹣1
0
1
2
…
y＝ax²+bx+c
…
t
m
2
2
n
…
且当x $= - \frac{1}{2}$ 时，与其对应的函数值y＜0，有以下结论：①abc＜0；②﹣2和3是关于x的方程ax²+bx+c＝t的两个根；③a $< - \frac{8}{3}$ ；④m+n $＞ - \frac{20}{3}$ .其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 在一个不透明的袋子里装有红球和白球共30个，这些球除颜色外其余都相同.小明通过多次试验发现，摸出白球的频率稳定在0.3左右，则袋子里可能有个红球.

查看试题解析
14. 位于贵州省的射电望远镜（FAT）（如图1）是目前世界上口径最大、精度最高的望远镜.根据有关资料显示，该望远镜的轴截面呈抛物线状，口径AB为500m，最低点P到口径面AB的距离是100m.若按如图2所示建立平面直角坐标系，则该抛物线的解析式为 .

查看试题解析
15. 如图，四边形ABCD为⊙O的内接正四边形，△AEF为⊙O的内接正三角形，连接DF.若DF恰好是同圆的一个内接正多边形的一边，则这个正多边形的边数为 .

查看试题解析
16. 如图，在平面直角坐标系中，将△ABO绕点B顺时针旋转到△A₁BO₁的位置，使点A的对应点A₁落在直线y＝ $\frac{\sqrt{3}}{3}$ x上，再将△A₁BO₁绕点A₁顺时针旋转到△A₁B₁Q₂的位置，使点O₁的对应点O₂落在直线y＝ $\frac{\sqrt{3}}{3}$ x上，依次进行下去…，若点A的坐标是（0，1），点B的坐标是（ $\sqrt{3}$ ， 1），则点A₁₂的横坐标是.

查看试题解析

三、解答题

17. 解方程：

(1)、（x﹣1）² $- \frac{100}{9} =$ 0；

(2)、2x²+8x﹣1＝0.

查看试题解析
18. △ABC在平面直角坐标系中的位置如图所示，已知A（﹣2，3），B（﹣3，1），C（﹣1，2）.

⑴画出△ABC绕点O逆时针旋转90°后得到的△A₁B₁C₁；

⑵画出△ABC关于原点O的对称图形△A₂B₂C₂；

⑶直接写出下列点的坐标：A₁ ， B₂ .

查看试题解析
19. 2019年某县投入100万元用于农村“扶贫工程”，计划以后每年以相同的增长率投入，2021年该县计划投入“扶贫工程”144万元.

(1)、求该县投入“扶贫工程”的年平均增长率；

(2)、若2022年保持从2019年到2021年的年平均增长率不变，求2022年该县将投入“扶贫工程”多少万元？

查看试题解析
20. 如图，已知直线y＝kx﹣3k（k≠0）与x轴、y轴分别交于点B，C，∠OBC＝45°.抛物线y＝ax²+bx+c（a≠0）经过点B，C，且经过点A（﹣1，0）.

(1)、求直线和抛物线的解析式；

(2)、请观察图象，直接写出当kx﹣3k≥ax²+bx+c时x的取值范围.

查看试题解析
21. 如图，有一座圆弧形拱桥，它的跨度 $A B$ 为 $60 m$ ，拱高 $P M$ 为 $18 m$ ，当洪水泛滥到跨度只有 $30 m$ 时，就要采取紧急措施，若某次洪水中，拱顶离水面只有 $4 m$ ，即 $P N = 4 m$ 时，试通过计算说明是否需要采取紧急措施.

查看试题解析
22. 黔西南州山川秀美、景色迷人，是中国西部一个黄金旅游区.为了奖励员工，某公司计划组织一次旅游活动，有以下四个地点供选择：A.花江铁索桥；B.马玲河峡谷；C.二十四道拐；D.万峰林.现随机调查了部分员工最想去的旅游地点，并根据调查结果绘制了如下两幅不完整的统计图.
请你根据统计图中的信息，解决下列问题：

(1)、这次调查一共抽取了名员工；扇形统计图中，旅游地点D所对应的扇形圆心角的度数为 .

(2)、请补全条形统计图.

(3)、在选择旅游地点C的员工中，甲、乙、丙、丁4人表现最为积极，现打算从这4人中任选2人作为本次旅游活动的策划员，请用列表或画树状图的方法求出恰好选中甲和乙的概率.

查看试题解析
23. 某服装批发市场销售一种衬衫，每件衬衫的进货价为50元，规定每件的售价不低于进货价.经市场调查，每月的销售量y（件）与每件的售价x（元）满足一次函数关系，部分数据如表：
售价x（元/件）
55
60
65
销售量y（件）
700
600
500

(1)、求出y与x之间的函数关系式；（不需要求自变量x的取值范围）

(2)、物价部门规定，该衬衫每件的利润不允许高于进货价的50%，设销售这种衬衫每月的总利润为w（元），求w与x之间的函数关系式，当每件衬衫的售价定为多少时，可获得最大利润？最大利润是多少？

查看试题解析
24. 如图，AB是⊙O的直径，点C，D在⊙O上，BD平分∠ABC，过点D作DE⊥BC，交BC的延长线于点E.

(1)、求证：DE是⊙O的切线；

(2)、若CE＝2，DE＝5，求⊙O的半径.

查看试题解析
25. 如图1，二次函数y＝a（x+3）（x﹣4）的图象交坐标轴于点A，B（0，﹣2），点P为x轴上一动点.

(1)、求该二次函数的解析式；

(2)、过点P作PQ⊥x轴，分别交线段AB、抛物线于点Q，C，连接AC.若OP＝1，求△ACQ的面积；

(3)、如图2，连接PB，将线段PB绕点P逆时针旋转90°得到线段PD.当点D在抛物线上时，求点D的坐标.

查看试题解析

x	…	﹣2	﹣1	0	1	2	…
y＝ax²+bx+c	…	t	m	2	2	n	…

售价x（元/件）	55	60	65
销售量y（件）	700	600	500