备考2022年中考数学一轮复习专题：探索图形的规律

试卷更新日期：2022-01-13 类型：一轮复习

进入出卷网下载

一、单选题

1. 如图，一串有趣的图案按一定规律排列，请仔细观察，按此规律第 $2021$ 个图案是（）

A、 B、 C、 D、

查看试题解析
2. 观察下列图形的规律，依照此规律第9个图形中共有（）个点．

A、135 B、140 C、145 D、150

查看试题解析
3. 如图五个正方形中各有四个数，各正方形中的四个数之间都有相同的规律，根据此规律，可推测出m的值为（）

A、0 B、1 C、4 D、8

查看试题解析
4. 在某学校庆祝建党“100周年”的活动上，宇阳同学用围棋棋子按照某种规律摆成如图所示的“100”字样．按照这种规律，第 $n$ 个“100”字样的棋子个数是（）

A、 $11 n$ B、 $n + 10$ C、 $5 n + 6$ D、 $6 n + 5$

查看试题解析
5. 如图是一组有规律的图案，它们是由大小相同的“ ”图案组成的，依此规律，第2021个图案中含有“ ”图案的个数为（）

A、10106 B、10105 C、11005 D、11006

查看试题解析
6. 下列图形是按一定规律排列的.依照此规律，第⑥个图形需（）根火柴棒

A、40 B、41 C、42 D、43

查看试题解析
7. 观察如下图形，它们是按一定规律排列的，依照次规律，第n的图形中共有210个小棋子，则n等于（）

A、20 B、21 C、15 D、16

查看试题解析
8. 将一半径相同的小圆按如图所示的规律摆放，第1个图形有4个小圆，第2个图形有8个小圆，第3个图形有14个小圆，…，依此规律，第9个图形的小圆个数是(　　)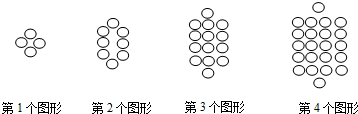

A、36 B、74 C、90 D、92

查看试题解析
9. 观察下列图形：

它们是按一定规律排列的，依照此规律，第 $20$ 个图形共有★个（）

A、 $63$ B、 $57$ C、 $68$ D、 $60$

查看试题解析
10. 下列图形都是有几个黑色和白色的正方形按一定规律组成，图①中有2个黑色正方形，图②中有5个黑色正方形，图③中有8个黑色正方形，图④中有11个黑色正方形，…，按此规律，图⑩中黑色正方形的个数是（）

A、32 B、29 C、28 D、26

查看试题解析

二、填空题

11. 观察如图图形的构成规律，依照此规律，第100个图形中共有个“•”．

查看试题解析
12. 观察下列图形：

它们是按一定规律排列的，依照此规律，用6064个五角星摆出的图案应该是第个图形.

查看试题解析
13. 动脑筋、找规律，李老师给小明出了下面的一道题，请根据数字排列的规律，探索下列问题：

(1)、在A处的数是正数还是负数；

(2)、负数排在A，B，C，D中的位置？

(3)、第2017个数是正数还是负数，排在对应于A，B，C，D中的位置？

查看试题解析
14. 如图，下面每个图形中的四个数都是按相同的规律填写的，根据此规律确定n的值为.

查看试题解析
15. 观察下列图形的构成规律，根据此规律，第10个图形中有个圆.

查看试题解析
16. 从图①中找出规律，并按规律从图②中找出 $a$ ， $b$ ， $c$ 的值，计算 $a + b - c$ 的值是．

查看试题解析

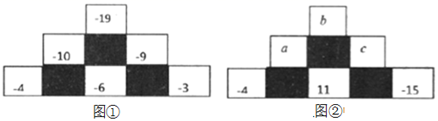
三、综合题

17. 观察下列图形，发现图形中“●”的排列规律：

根据你所发现的规律，解答下列问题．

(1)、在题中横线上补画出第1个图形；

(2)、把第1个图形中“●”的个数记为a₁ ，第2个图形中“●”的个数记为a₂ ，第3个图形中“●”的个数记为a₃ ， …，第n个图形中“●”的个数记为a_n（其中n为正整数）．
①直接写出：第5个图形中“●”的个数a₅=▲ ；

②计算：a₂-a₁−=▲ ， a₃-a₂=▲ ， a₄-a₃−=▲ ；

③由②中的计算结果猜想a_n+1-a_n=▲ ；（用含有n的式子表示）

④模仿②中的方法，猜想a_n+1+a_n ，的结果（用含有n的式子表示），并写出猜想过程．

查看试题解析
18. 下面的图形是边长为 $1 cm$ 的正方形按照某种规律排列而组成的．

(1)、观察图形，填写下表：

图形

①

②

③

正方形的个数

8

18

图形的周长

(2)、推测第 $n$ 个图形中，正方形的个数为多少？周长为多少？

(3)、第2021个图形中，正方形的个数是多少？

查看试题解析
19. 用火柴棒按图中的方式搭图形：

按图示规律填空：

图形标号

①

②

③

④

⑤

火柴棒根数

5

9

13

a

b

(1)、 $a =$ ， $b =$ ；

(2)、按照这种方式搭下去，则搭第n个图形需要火柴棒的根数为；（用含n的代数式来表示）

(3)、按照这种方式搭下去，用（2）中的代数式求第2021个图形需要的火柴棒根数．

查看试题解析
20. 把黑色三角形按如图所示的规律拼图案，其中第①个图案中有1个黑色三角形，第②个图案中有3个黑色三角形，第③个图案中有6个黑色三角形……按此规律排列下去，解答下列问题：

(1)、填写下列表格：

图序

①

②

③

④

…

黑色三角形个数

1

3

6

…

(2)、若第n个图案中黑色三角形的个数有91个，求 $n$ 的值．

查看试题解析
21. 将一些半径相同的小圆按如图所示的规律摆放：

(1)、填写下表：

图形序号

1

2

3

4

5

小圆个数

6

10

16

(2)、照这样的规律摆放，第99个这样的图形需要个小圆；

(3)、第n个这样的图形需要个小圆.

查看试题解析
22. 小丽在用等长的木棒设计图案，她先用 $8$ 根木棒摆成图案①，再按图案①的个数逐渐增加 $1$ 的规律拼成下图中的图案②和图案③.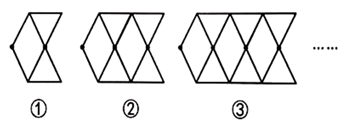

(1)、她在摆第 $5$ 个图案时，用了多少根木棒？

(2)、请你帮她用含 $n$ 的代数式表示第 $n$ 个图案所需木棒的根数.

(3)、如果要摆出第 $50$ 个图案，所需木棒的根数是多少？

查看试题解析
23. 下列是用火柴棒拼出的一列图形．

仔细观察，找出规律，解答下列各题：

(1)、第4个图形中共有根火柴，第6个图形中共有根火柴；

(2)、第n个图形中共有根火柴（用含n的式子表示）；

(3)、请判断上组图形中前2021个图形火柴总数是2021的倍数吗？请说明理由．
（参考： $1 + 2 + 3 + \dots + n = \frac{(1 + n) \times n}{2}$ ，例如求解 $1 + 2 + 3 + \dots + 9 = \frac{(1 + 9) \times 9}{2} = 45$ ）

查看试题解析
24. （规律探索）用同样大小的两种不同颜色的正方形纸片，按如图方式拼成长方形：

第（1）个图形中有2张正方形纸片；

第（2）个图形中有2（1+2）=6=2×3张正方形纸片；

第（3）个图形中有2（1+2+3）=12=3×4张正方形纸片；

第（4）个图形中有2（1+2+3+4）=20=4×5张正方形纸片；

请你观察上述图形与算式，完成下列问题：

（规律归纳）

(1)、第（6）个图形中有张正方形纸片（直接写出结果）；

(2)、根据上面的发现我们可以猜想：1+2+3+…+n= （用含n的代数式表示）；

(3)、（规律应用）根据你的发现计算：121+122+123+…+400．

查看试题解析
25. 观察下面的点阵图和相应的等式，探究其中的规律：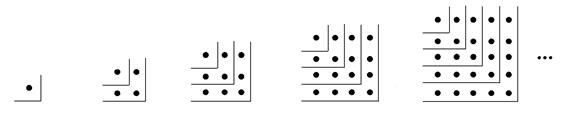

(1)、在④和⑤后面的横线上分别写出相应的等式：
①1＝1²；②1＋3＝2²；③1＋3＋5＝3²；④；⑤；….

(2)、通过猜想写出与第n个点阵图相对应的等式．

查看试题解析
26. 如图，是一组完全相同的黑白小球组成的图形

观察上面各图及对应的关系式，根据发现的规律，解决下列问题：

(1)、写出第6个等式：；

(2)、写出你猜想的第n个等式：（用含 $n$ 的等式表示，并证明其符合题意性）

查看试题解析
27. 如图是一组有规律的图案，它们是由边长相等的等边三角形组合而成，第1个图案有4个三角形，第2个图案有7个三角形，第3个图案有10个三角形…照此规律摆下去：

(1)、照此规律，摆成第5个图案需要个三角形．

(2)、照此规律，摆成第n个图案需要个三角形．（用含n的代数式表示）

(3)、照此规律，摆成第2020个图案需要几个三角形？

查看试题解析
28. 如下图是组有规律的图案，第1个图案由4个基础图形“ ”组成，第2个图案由7个基础图形组成，……

(1)、填表：

第n个图案

1

2

3

4

…

基础图形个数

4

7

…

(2)、试写出第（n是正整数）个图案是由个基础图形组成

(3)、若第n个图案共有基础图形2017个，则n的值是多少？

查看试题解析

图形	①	②	③
正方形的个数	8		18
图形的周长

图形标号	①	②	③	④	⑤
火柴棒根数	5	9	13	a	b

图序	①	②	③	④	…
黑色三角形个数	1	3	6		…

图形序号	1	2	3	4	5
小圆个数	6	10	16