备考2022年中考数学一轮复习专题：探索数与式的规律

试卷更新日期：2022-01-13 类型：一轮复习

进入出卷网下载

一、单选题

1. 已知： $\sqrt{2 + \frac{2}{3}} = 2 \sqrt{\frac{2}{3}}$ ， $\sqrt{3 + \frac{3}{8}} = 3 \sqrt{\frac{3}{8}}$ ， $\sqrt{4 + \frac{4}{15}} = 4 \sqrt{\frac{4}{15}}$ ， $\sqrt{5 + \frac{5}{24}} = 5 \sqrt{\frac{5}{24}}$ ，若 $\sqrt{10 + \frac{b}{a}} = 10 \sqrt{\frac{b}{a}}$ 符合上面规律，则a+b的值为（）

A、179 B、109 C、210 D、104

查看试题解析
2. 正六边形ABCDEF在数轴上的位置如图，点A、F对应的数分别为0和1，若正六边形ABCDEF绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点E所对应的数为2，则连续翻转2021次后，数轴上2021这个数所对应的点是（）

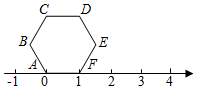A、A点 B、B点 C、C点 D、D点

查看试题解析
3. 按下列规律排成一列数： $\frac{1}{1}$ 、 $\frac{1}{2}$ 、 $\frac{2}{1}$ 、 $\frac{1}{3}$ 、 $\frac{2}{2}$ 、 $\frac{3}{1}$ 、 $\frac{1}{4}$ 、 $\frac{2}{3}$ 、 $\frac{3}{2}$ 、 $\frac{4}{1}$ 、 $\frac{1}{5}$ 、……，则第（）个数是 $\frac{2}{101}$

A、5051 B、5052 C、5152 D、5153

查看试题解析
4. 一本书的页码从1记到n，把所有这些页码加起来，其中漏加了一页，结果得出了不正确的和2021，这个被漏加的页码是（）

A、5 B、20 C、59 D、63

查看试题解析
5. 观察下列等式： $7^{0} = 1$ ， $7^{1} = 7$ ， $7^{2} = 49$ ， $7^{3} = 343$ ， $7^{4} = 2401$ ， $7^{5} = 16807$ ，…根据其中的规律可得 $7^{0} + 7^{1} + \dots + 7^{2022}$ 的结果的个位数字是（）

A、0 B、1 C、7 D、8

查看试题解析
6. 仔细观察，探究规律：
$(x - 1) (x + 1) = x^{2} - 1$

$(x - 1) (x^{2} + x + 1) = x^{3} - 1$

$(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$

$(x - 1) (x^{4} + x^{3} + x^{2} + x + 1) = x^{5} - 1$

则算式 $2^{0} + 2^{1} + 2^{2} + 2^{3} + \dots + 2^{2021}$ 值的个位数字为（）

A、1 B、3 C、5 D、7

查看试题解析
7. 如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着-3，-2，-1，0，且任意相邻四个台阶上的数的和都相等，则前37个台阶上的数的和是（）

A、-3 B、-48 C、-57 D、-51

查看试题解析
8. 观察下列各式：3¹＝3，3²＝9，3³＝27，3⁴＝81，3⁵＝243，3⁶＝729，…则：3²⁰²¹的个位数字是（　　）

A、3 B、9 C、7 D、1

查看试题解析
9. 观察下列算式：2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，2⁶＝64，2⁷＝128，2⁸＝256…，则2＋2²＋2³＋2⁴＋2⁵＋…＋2²⁰²⁴的末位数字是（）

A、8 B、6 C、4 D、0

查看试题解析
10. “书法艺术课”开课后，某同学买了一包纸练习软笔书法，且每逢星期几写几张，即每星期一写1张，每星期二写2张，……，每星期日写7张，若该同学从某年的5月1日开始练习，到5月30日练习完后累积写完的宣纸总数超过120张，请推断出5月30日可能是星期几（）

A、二、三、四 B、三、四、五 C、四、五、六 D、五、六、日

查看试题解析

二、填空题

11. 将相同的长方形卡片按如下方式摆放在一个直角上，每个长方形卡片长为2，宽为1，依此类推，当摆放2021个这样的长方形时，实线部分长为．

查看试题解析
12. 观察下列等式： $7^{0} = 1$ ， $7^{1} = 7$ ， $7^{2} = 49$ ， $7^{3} = 343$ ， $7^{4} = 2401$ ， $7^{5} = 16807$ ，…，根据其中的规律可得 $7^{0} + 7^{1} + 7^{2} + \dots + 7^{2021}$ 的结果的个位数字是．

查看试题解析

13. 有一种密码，将英文26个字母

a

、

b

、

c

、…、

z

（不论大小写）依次对应1、2、3、…、26，这26个自然数（见表格），当明码对应的序号

x

为奇数时，密码对应的序号为

\frac{| x - 25 |}{2}

，当明码对应的序号

x

偶数时，密码对应的序号为

\frac{x}{2} + 3

，按上述规定，将明码“

a g f o

”译成密码是．

字母	$a$	$b$	$c$	$d$	$e$	$f$	$g$	$h$	$i$	$j$	$k$	$l$	$m$
序号	1	2	3	4	5	6	7	8	9	10	11	12	13
字母	$n$	$o$	$p$	$q$	$r$	$s$	$t$	$u$	$v$	$w$	$x$	$y$	$z$
序号	14	15	16	17	18	19	20	21	22	23	24	25	26

查看试题解析

14. 如图所示的运算程序中，皆开始输入x的值为48，第一次输出的结果是24，第二次输出的结果是12，第三次输出的结果是6，……则第2021次输出的结果为．

查看试题解析
15. 请看杨辉三角 $(1)$ ，并观察等式 $(2)$

根据前面各式的规律，则你猜想 ${(a + b)}^{6}$ 的展开式中含 $a^{2} b^{4}$ 项的系数是．

查看试题解析
16. 如图，一个粒子在第一象限内及x轴、y轴上运动，在第一分钟，它从原点运动到点（1，0），第二分钟，它从点（1，0）运动到点（1，1），而后它接着按图中箭头所示在与x轴，y轴平行的方向上来回运动，且每分钟移动1个单位长度，那么在第2022分钟时，这个粒子所在位置的坐标是．

查看试题解析

三、综合题

17. 有一列数，第一个数用 $a_{1}$ 表示，第二个数用 $a_{2}$ 表示，…，第n个数用 $a_{n}$ 表示，n为正整数；已知 $a_{1} = 1 + \frac{2}{1}$ ， $a_{2} = 1 + \frac{2}{2}$ ， $a_{3} = 1 + \frac{2}{3}$ ， $a_{4} = 1 + \frac{2}{4}$ ，…….

(1)、利用以上运算的规律，写出 $a_{n}$ =；

(2)、计算： $a_{1} \cdot a_{2} \cdot a_{3} \cdot \dots a_{100}$ 的值.

查看试题解析
18. 观察下面三行：
-3，9，-27，81，…①

1，-3，9，-27，…②

-2，10，-26，82…③

(1)、第①行的数按什么规律排列？

(2)、第②③行数与第①行数分别有什么关系？

(3)、取每行数的第7个数，计算这三个数的和．

查看试题解析

19. 将图1中的正方形剪开得到图2，则图2中共有4个正方形；将图2中的一个正方形剪开得到图3，图3中共有7个正方形；将图3中4个较小的正方中的一个剪开得到图4，则图4中共有10个正方形，照这个规律剪下去……

(1)、根据图中的规律补全下表：

图形标号	1	2	3	4	5	6	…	n
正方形个数	1	4	7	10			…

(2)、求第几幅图形中有2020个正方形？

查看试题解析

20. 找规律：
一次足球比赛中，有n（n≥2）个球队参加比赛，假设此次比赛为单循环比赛（参加比赛的每一个队都与其他所有的队各赛一场），球队总数与总的比赛场数如表．

球队数（n）

2

3

4

5

6

比赛场数

1

3

6

10

15

(1)、8个球队总共比赛的总场数为．

(2)、当有n个球队参加时，共比多少场？

(3)、当n＝10时，共有多少场比赛？

查看试题解析
21. 一列数a₁ ， a₂ ， a₃ ， …，a_n ，其中a₁＝﹣1，a₂＝ $\frac{1}{1 - a_{1}}$ ，a₃＝ $\frac{1}{1 - a_{2}}$ ，…，a_n＝ $\frac{1}{1 - a_{n - 1}}$ .

(1)、求a₂ ， a₃的值；

(2)、求a₁+a₂+a₃+…+a₂₀₂₁的值.

查看试题解析
22. 观察下列单项式： $x$ ， $- 3 x^{2}$ ， $5 x^{3}$ ， $- 7 x^{4}$ ，…， $37 x^{19}$ ， $- 39 x^{20}$ ，…写出第 $n$ （ $n$ 为正整数）个单项式.为了解这个问题，特提供下面的解题思路.

(1)、请你写出第六项的系数是什么？第七项的次数是什么？

(2)、请你根据猜想，写出第2021个单项式是什么？第 $n$ 个单项式是什么？

查看试题解析
23. 探究：
第1个： $2^{2} - 2^{1} = 2 \times 2^{1} - 1 \times 2^{1} = 2^{1}$ ，

第2个： $2^{3} - 2^{2} = 2 \times 2^{2} - 1 \times 2^{2} = 2^{2}$ ，

第3个： $2^{4} - 2^{3} = 2 \times 2^{3} - 1 \times 2^{3} = 2^{3}$ ，

……

(1)、请仔细观察，写出第6个等式；

(2)、请你找规律，写出第n个等式；

(3)、计算： $2^{1} + 2^{2} + 2^{3} + \dots 2^{2019} + 2^{2020} - 2^{2021}$ ．

查看试题解析
24. 观察下列各算式： $1 + 3 = 4 = 2^{2} ， 1 + 3 + 5 = 9 = 3^{2} ， 1 + 3 + 5 + 7 = 16 = 4$ ．

(1)、试猜想： $1 + 3 + 5 + 7 + \dots + 2005 + 2007$ 的值？

(2)、推广： $1 + 3 + 5 + 7 + 9 + \dots + (2 n - 1) + (2 n + 1)$ 的和是多少？

查看试题解析
25. 观察下面各式的规律：
1²+（1×2）²+2²＝（1×2+1）²；

2²+（2×3）²+3²＝（2×3+1）²；

3²+（3×4）²+4²＝（3×4+1）²；

…

(1)、写出第2021个式子；

(2)、写出第n个式子，并验证你的结论．

查看试题解析
26. 观察下列等式，探究其中的规律并解答问题：

1＝1²

2+3+4＝3²

3+4+5+6+7＝5²

4+5+6+7+8+9+10＝k²

(1)、第4个等式中，k＝；

(2)、写出第s个等式：；

(3)、写出第n个等式：（其中n为正整数）

查看试题解析
27. 下面的图形是边长为 $1 cm$ 的正方形按照某种规律排列而组成的．

(1)、观察图形，填写下表：

图形

①

②

③

正方形的个数

8

18

图形的周长

(2)、推测第 $n$ 个图形中，正方形的个数为多少？周长为多少？

(3)、第2021个图形中，正方形的个数是多少？

查看试题解析
28. 先阅读材料，再解决问题．
⑴ $\sqrt{1^{3}} = \sqrt{1^{2}} = 1$

⑵ $\sqrt{1^{3} + 2^{3}} = \sqrt{3^{2}} = 3$

⑶ $\sqrt{1^{3} + 2^{3} + 3^{3}} = \sqrt{6^{2}} = 6$

⑷ $\sqrt{1^{3} + 2^{3} + 3^{3} + 4^{3}} = \sqrt{10^{2}} = 10$

…

根据上面的规律，解决问题：

(1)、 $\sqrt{1^{3} + 2^{3} + 3^{3} + 4^{3} + 5^{3} + 6^{3}}$ ==

(2)、 $\sqrt{1^{3} + 2^{3} + 3^{3} + \dots + n^{3}}$ （用含n的代数式表示）．

查看试题解析
29. 观察下列各式的规律：
① $1 \times 4 - 2^{2} = 0$ ；② $2 \times 5 - 3^{2} = 1$ ；③ $3 \times 6 - 4^{2} = 2$ ；…

根据上述式子的规律，解答下列问题：

(1)、第④个等式为.

(2)、写出第n个等式，并验证其正确性.

查看试题解析
30. 用数学猜想解决问题
数学猜想即依据已知条件或已有结论，运用实验、观察、归纳、类比的方法，对研究的问题做出由特殊到一般的归纳推测．数学猜想是解决问题的常用方法，也是数学发展的重要思维式．

观察下列等式回答问题：

第一个等式： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$

第二个等式： $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$

第三个等式： $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$

第四个等式： $\frac{1}{4 \times 5} = \frac{1}{4} - \frac{1}{5}$

(1)、由已知等式可猜想第n个等式为： $\frac{1}{n (n + 1)} =$ ．

(2)、求 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{n (n + 1)}$ 的值（要求写出过程，结果用含n的代数式表示）

查看试题解析

球队数（n）	2	3	4	5	6
比赛场数	1	3	6	10	15

图形	①	②	③
正方形的个数	8		18
图形的周长