备考2022年中考数学一轮复习专题:相似三角形及其应用
试卷更新日期:2022-01-13 类型:一轮复习
一、单选题
-
1. 若 , 则等于( )A、 B、 C、 D、2. 如图,直线a,b,c被直线 , 所截,交点分别为点A,C,E和点B,D,F.已知 , 且 , , 则的值是( )
 A、 B、 C、 D、3. 如图,以点为位似中心,把放大为原图形的2倍得到 , 若与的位似比为 , 则以下结论中正确的是( )
A、 B、 C、 D、3. 如图,以点为位似中心,把放大为原图形的2倍得到 , 若与的位似比为 , 则以下结论中正确的是( )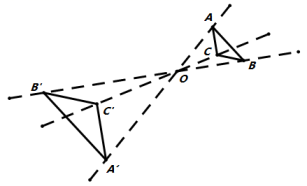 A、 B、 C、 D、4. 如图,在平行四边形中,点在边上, ,连接交于点 , 则的面积与的面积之比为( )
A、 B、 C、 D、4. 如图,在平行四边形中,点在边上, ,连接交于点 , 则的面积与的面积之比为( )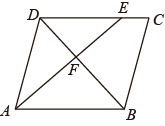 A、 B、 C、 D、5. 如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )
A、 B、 C、 D、5. 如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( ) A、2cm B、5cm C、6cm D、7cm6. 如图,在四边形ABCD中,BC∥AD,∠ADC=90°,点E沿着A→B→C的路径以2cm/s的速度匀速运动,到达点C停止运动,EF始终与直线AB保持垂直,与AD或DC交于点F,记线段EF的长度为dcm,d与时间t的关系图如图所示,则图中a的值为( )
A、2cm B、5cm C、6cm D、7cm6. 如图,在四边形ABCD中,BC∥AD,∠ADC=90°,点E沿着A→B→C的路径以2cm/s的速度匀速运动,到达点C停止运动,EF始终与直线AB保持垂直,与AD或DC交于点F,记线段EF的长度为dcm,d与时间t的关系图如图所示,则图中a的值为( )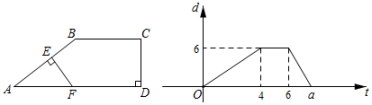 A、7.5 B、7.8 C、9 D、9.67. 如图,在中, , , 为边上的一点,且.若的面积为 , 则的面积为( )
A、7.5 B、7.8 C、9 D、9.67. 如图,在中, , , 为边上的一点,且.若的面积为 , 则的面积为( )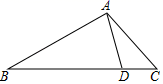 A、 B、 C、 D、8. 如图▱ABCD,F为BC中点,延长AD至E,使 , 连结EF交DC于点G,则=( )
A、 B、 C、 D、8. 如图▱ABCD,F为BC中点,延长AD至E,使 , 连结EF交DC于点G,则=( ) A、2:3 B、3:2 C、9:4 D、4:99. 如图, , 相交于点 ,且 ,点 , , 在同一条直线上.已知 , , ,则 , , 之间满足的数量关系式是( )
A、2:3 B、3:2 C、9:4 D、4:99. 如图, , 相交于点 ,且 ,点 , , 在同一条直线上.已知 , , ,则 , , 之间满足的数量关系式是( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,正方形 与正方形 是以原点 为位似中心的位似图形,且相似比为 ,点 , , 在 轴上,若正方形 的边长为6,则 点坐标为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,正方形 与正方形 是以原点 为位似中心的位似图形,且相似比为 ,点 , , 在 轴上,若正方形 的边长为6,则 点坐标为( )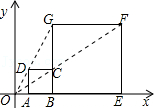 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 点C是线段AB的黄金分割点, , 如果线段AB的长度为2,则AC的长为 .12. 若两个相似三角形的相似比是5:7,则它们的对应高线的比是 .13. 如图,点在的边上,要判断 , 还请你添加一个条件:.
 14. 已知 , 则.15. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果CD=4,那么AD•BD的值是.
14. 已知 , 则.15. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果CD=4,那么AD•BD的值是.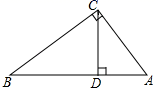 16. 七边形位似于七边形 , 它们的面积比为4∶9,已知位似中心O到A的距离为6,那么O到的距离为.
16. 七边形位似于七边形 , 它们的面积比为4∶9,已知位似中心O到A的距离为6,那么O到的距离为.三、综合题
-
17. 如图1,在△ABC中,AB=AC=10,tanB= , 点D为BC边上的动点(点D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
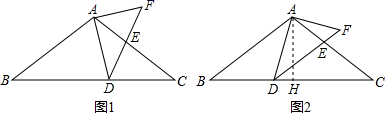 (1)、求证:△ABD∽△DCE;(2)、当AB∥DE时(如图2),求AE的长.(提示:过点A作AH⊥BC交BC于点H)18. 如图,为锐角三角形,是边上的高,正方形的一边在上,顶点G,H分别在 , 上,已知 , .
(1)、求证:△ABD∽△DCE;(2)、当AB∥DE时(如图2),求AE的长.(提示:过点A作AH⊥BC交BC于点H)18. 如图,为锐角三角形,是边上的高,正方形的一边在上,顶点G,H分别在 , 上,已知 , . (1)、求证:;(2)、求正方形的面积19. 如图,平面直角坐标系中, 是坐标原点,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 坐标是 .抛物线与 轴交于点 ,点 是抛物线的顶点,连接 .
(1)、求证:;(2)、求正方形的面积19. 如图,平面直角坐标系中, 是坐标原点,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 坐标是 .抛物线与 轴交于点 ,点 是抛物线的顶点,连接 . (1)、求抛物线的解析式并直接写出顶点 的坐标.(2)、直线 与抛物线对称轴交于点 ,点 为直线 上一动点.
(1)、求抛物线的解析式并直接写出顶点 的坐标.(2)、直线 与抛物线对称轴交于点 ,点 为直线 上一动点.①当 的面积等于 面积的2倍时,求点 的坐标;
②在①的条件下,当点 在 轴上方时,过点 作直线 垂直于 ,直线 交直线 于点 ,点 在直线 上,且 时,求 的长.
20. 如图,在 ABC中,AB=AC,∠A为锐角且不等于60°,AD平分∠BAC交BC于点D,BE⊥AC于点E,AD交BE于点F.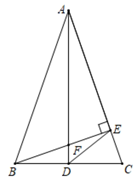 (1)、写出图中所有与 ACD相似的三角形(全等除外);(2)、连接DE,求证: ABF∽△EDF.21. 如图,在△ABC中,点D、E分别在边AB、AC上,∠AED=∠B,AG平分∠BAC,线段AG分别交线段DE、BC于点F、G.
(1)、写出图中所有与 ACD相似的三角形(全等除外);(2)、连接DE,求证: ABF∽△EDF.21. 如图,在△ABC中,点D、E分别在边AB、AC上,∠AED=∠B,AG平分∠BAC,线段AG分别交线段DE、BC于点F、G. (1)、求证: ;(2)、若 ,求 的值;22. 如图1,在 中, , , 是 的中点.过点 作射线 交 于点 (点 不与点 重合),过点 作 于点 ,连接 ,过点 作 交 于点 .
(1)、求证: ;(2)、若 ,求 的值;22. 如图1,在 中, , , 是 的中点.过点 作射线 交 于点 (点 不与点 重合),过点 作 于点 ,连接 ,过点 作 交 于点 .
 (1)、求证: ;(2)、如图2,若 ,连接 并延长到点 ,使 ,连接 , ,求证:四边形 为菱形;(3)、在(2)的条件下,求 的值.23. 如图,矩形 中, 为 上一点, 于点 .
(1)、求证: ;(2)、如图2,若 ,连接 并延长到点 ,使 ,连接 , ,求证:四边形 为菱形;(3)、在(2)的条件下,求 的值.23. 如图,矩形 中, 为 上一点, 于点 . (1)、证明 ;(2)、若 , , ,求 的长.24. 如图,在 和 中, , ,且 ,线段AC与DE交于点G,连接BD,CE.
(1)、证明 ;(2)、若 , , ,求 的长.24. 如图,在 和 中, , ,且 ,线段AC与DE交于点G,连接BD,CE. (1)、如图1,当B,D,E三点共线时,求证: ;(2)、如图2,当B,D,E三点不共线时,延长ED交BC于点F,求证: .25. 如图,在 中, ,AC、BC的长恰好为方程 的两根,且 ,D为AB的中点.
(1)、如图1,当B,D,E三点共线时,求证: ;(2)、如图2,当B,D,E三点不共线时,延长ED交BC于点F,求证: .25. 如图,在 中, ,AC、BC的长恰好为方程 的两根,且 ,D为AB的中点. (1)、求a的值.(2)、动点P从点A出发,沿A→D→C的路线向点C运动;点Q从点B出发,沿B→C的路线向点C运动.若点P、Q同时出发,速度都为每秒2个单位,当点P经过点D时,点P速度变为每秒3单位,同时点Q速度变为每秒1个单位.当其中有一点到达终点时整个运动随之结束.设运动时间为t秒.在整个运动过程中,设 的面积为S,试求S与t之间的函数关系式;并指出自变量t的取值范围.26. 如图,在平行四边形ABCD中,AD=AC,∠ADC=α,点E为射线BA上一动点,且AE<AB,连接DE,将线段DE所在直线绕点D顺时针旋转α交BA延长线于点H,DE所在直线与射线CA交于点G.
(1)、求a的值.(2)、动点P从点A出发,沿A→D→C的路线向点C运动;点Q从点B出发,沿B→C的路线向点C运动.若点P、Q同时出发,速度都为每秒2个单位,当点P经过点D时,点P速度变为每秒3单位,同时点Q速度变为每秒1个单位.当其中有一点到达终点时整个运动随之结束.设运动时间为t秒.在整个运动过程中,设 的面积为S,试求S与t之间的函数关系式;并指出自变量t的取值范围.26. 如图,在平行四边形ABCD中,AD=AC,∠ADC=α,点E为射线BA上一动点,且AE<AB,连接DE,将线段DE所在直线绕点D顺时针旋转α交BA延长线于点H,DE所在直线与射线CA交于点G.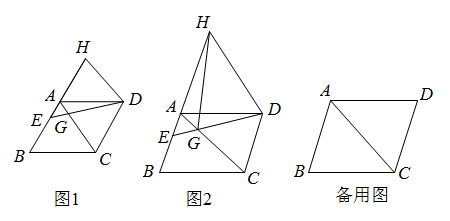 (1)、如图1,当α=60°时,求证:△ADH≌△CDG;(2)、当α≠60°时,
(1)、如图1,当α=60°时,求证:△ADH≌△CDG;(2)、当α≠60°时,①如图2,连接HG,求证:△ADC∽△HDG;
②若AB=9,BC=12,AE=3,请直接写出EG的长.
