备考2022年中考数学一轮复习专题:圆的综合
试卷更新日期:2022-01-13 类型:一轮复习
一、单选题
-
1. 如图,△ABC是一张周长为18cm的三角形纸片,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,若剪下的三角形的周长为8cm,则BC为( )
 A、8cm B、5cm C、6.5cm D、无法确定2. 已知点 , ,如果⊙A的半径为2,⊙B的半径为7,那么⊙A与⊙B的位置关系( )A、内切 B、外切 C、内含 D、外离3. 如图,半圆O的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是 ()
A、8cm B、5cm C、6.5cm D、无法确定2. 已知点 , ,如果⊙A的半径为2,⊙B的半径为7,那么⊙A与⊙B的位置关系( )A、内切 B、外切 C、内含 D、外离3. 如图,半圆O的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是 ()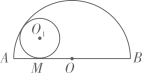 A、 B、 C、 D、4. 如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2 , 连接AO1并延长交⊙O1于点C,则∠ACO2的度数为( )
A、 B、 C、 D、4. 如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2 , 连接AO1并延长交⊙O1于点C,则∠ACO2的度数为( )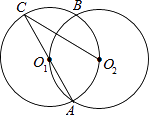 A、60° B、45° C、30° D、20°5. 如图, 的内切圆 与 分别相切于点D , E , F , 连接 , , , , ,则阴影部分的面积为( )
A、60° B、45° C、30° D、20°5. 如图, 的内切圆 与 分别相切于点D , E , F , 连接 , , , , ,则阴影部分的面积为( ) A、 B、 C、 D、6. 一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A、 B、 C、 D、6. 一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )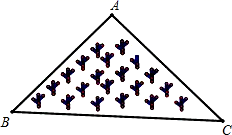 A、 ABC 的三条中线的交点 B、 ABC 三边的垂直平分线线的交点 C、 ABC 三条角平分线的交点 D、 ABC 三条高所在直线的交点7. 如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC=( )
A、 ABC 的三条中线的交点 B、 ABC 三边的垂直平分线线的交点 C、 ABC 三条角平分线的交点 D、 ABC 三条高所在直线的交点7. 如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC=( )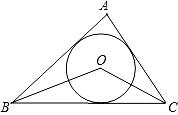 A、130° B、100° C、50° D、65°8. 下列四个命题:①直角三角形斜边上的中线等于斜边的一半;②对角线相等的平行四边形是菱形;⑨一组邻边相等的矩形是正方形;④三角形三条角平分线的交点是三角形的外心.其中真命题共有( )A、1个 B、2个 C、3个 D、4个9. 如图, 中, ,点 是 的内心,则 的度数为( )
A、130° B、100° C、50° D、65°8. 下列四个命题:①直角三角形斜边上的中线等于斜边的一半;②对角线相等的平行四边形是菱形;⑨一组邻边相等的矩形是正方形;④三角形三条角平分线的交点是三角形的外心.其中真命题共有( )A、1个 B、2个 C、3个 D、4个9. 如图, 中, ,点 是 的内心,则 的度数为( ) A、 B、 C、 D、10. 根据尺规作图的痕迹,可以判定点O为 的内心的是( )A、
A、 B、 C、 D、10. 根据尺规作图的痕迹,可以判定点O为 的内心的是( )A、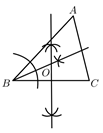 B、
B、 C、
C、 D、
D、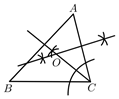
二、填空题
-
11. 已知一个三角形的三边长分别为5、7、8,则其内切的半径为 .12. 如图,已知圆O为 的内切圆,切点分别为D、E、F,且 , , ,则圆O的半径为 .
 13. 若三角形的面积是24cm2 , 周长是24cm,则这个三角形内切圆的半径是 cm.14. 若方程x2-7x+12=0的两个根分别是直角三角形两直角边的长,则这个直角三角形的内切圆半径为.15. 如图,等腰△ABC中,AB=AC,P为其底角平分线的交点,将△BCP沿CP折叠,使B点恰好落在AC边上的点D处,若DA=DP,则∠A的度数为.
13. 若三角形的面积是24cm2 , 周长是24cm,则这个三角形内切圆的半径是 cm.14. 若方程x2-7x+12=0的两个根分别是直角三角形两直角边的长,则这个直角三角形的内切圆半径为.15. 如图,等腰△ABC中,AB=AC,P为其底角平分线的交点,将△BCP沿CP折叠,使B点恰好落在AC边上的点D处,若DA=DP,则∠A的度数为. 16. 如图,⊙O是等边△ABC的内切圆,分别切AB , BC , AC于点E , F , D , P是 上一点,则∠EPF的度数是 .
16. 如图,⊙O是等边△ABC的内切圆,分别切AB , BC , AC于点E , F , D , P是 上一点,则∠EPF的度数是 .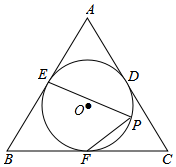
三、综合题
-
17. 如图,ΔABC是直角三角形,∠C=90°.
 (1)、请作出ΔABC的内切圆⊙O(尺规作图,不写作法,保留作图痕迹).(2)、设(1)中作出的⊙O与边AB,BC,CA分别相切于点D,E,F,BC=8,AC=6,①∠AOB=°;②BD=.18. 如图, 是 的外接圆,点E是 的内心,AE的延长线交BC于点F,交 于点D,连接BD,BE.
(1)、请作出ΔABC的内切圆⊙O(尺规作图,不写作法,保留作图痕迹).(2)、设(1)中作出的⊙O与边AB,BC,CA分别相切于点D,E,F,BC=8,AC=6,①∠AOB=°;②BD=.18. 如图, 是 的外接圆,点E是 的内心,AE的延长线交BC于点F,交 于点D,连接BD,BE. (1)、求证: ;(2)、若 , ,求DB的长.19. 如图,在 中, , , 是 的外接圆,连接 并延长交 于点 ,连接 ,点 是 的内心.
(1)、求证: ;(2)、若 , ,求DB的长.19. 如图,在 中, , , 是 的外接圆,连接 并延长交 于点 ,连接 ,点 是 的内心. (1)、请用直尺和圆规作出点 ,证明 ;(2)、求线段 长.20. 如图,点M是 的内心,BM的延长线和 的外接圆相交于D , 连接DC、DA、MA、MC , 四边形MADC是平行四边形.
(1)、请用直尺和圆规作出点 ,证明 ;(2)、求线段 长.20. 如图,点M是 的内心,BM的延长线和 的外接圆相交于D , 连接DC、DA、MA、MC , 四边形MADC是平行四边形. (1)、求证:MA=MC .(2)、若 ,则请直接写出弧 的长为 . (结果保留 )21. 如图,在 中, 平分 交 于E,D是 边上一动点,连接 交 于点P,连接 .已知 ,设B,D两点间的距离为 ,B,P两点间的距离为 ,A,P两点间的距离为 .
(1)、求证:MA=MC .(2)、若 ,则请直接写出弧 的长为 . (结果保留 )21. 如图,在 中, 平分 交 于E,D是 边上一动点,连接 交 于点P,连接 .已知 ,设B,D两点间的距离为 ,B,P两点间的距离为 ,A,P两点间的距离为 .小华根据学习函数的经验,分别对函数 随自变量x的变化而变化的规律进行了探究.

下面是小华的探究过程,请补充完整.
(1)、按照表中自变量x的值进行取点、画图、测量,分别得到了 为与x的几组对应值,如下表:0
1
2
3
4
5
6
2.49
2.64
2.88
3.25
3.80
4.65
6.00
4.59
4.24
3.80
3.25
2.51
0.00
并在平面直角坐标系 中画出了 的图象,如图所示:

①请在同一平面直角坐标系中画出函数 的图象;
②表格中空缺的数据约为 ▲ .
(2)、继续在同一坐标系中,画出所需要的函数图象,并结合函数图象直接写出:当 时, 长度的近似值约为 (结果保留两位小数):(3)、小华继续探究,得到:当 平分 时, 的长度是一个确定的值,请直接写出此时 的长度.22. 如图, 是△ABC的外心,I是△ABC的内心,连AI并延长交BC和⊙O于D、E两点. (1)、求证:EB=EI;(2)、若AB=4,AC=3,BE=2,求AI的长.23. 在梯形ABCD中,AD∥BC , AB⊥BC , AD=3,CD=5,cosC= (如图).M是边BC上一个动点(不与点B、C重合),以点M为圆心,CM为半径作圆,⊙M与射线CD、射线MA分别相交于点E、F .
(1)、求证:EB=EI;(2)、若AB=4,AC=3,BE=2,求AI的长.23. 在梯形ABCD中,AD∥BC , AB⊥BC , AD=3,CD=5,cosC= (如图).M是边BC上一个动点(不与点B、C重合),以点M为圆心,CM为半径作圆,⊙M与射线CD、射线MA分别相交于点E、F . (1)、设CE= ,求证:四边形AMCD是平行四边形;(2)、联结EM , 设∠FMB=∠EMC , 求CE的长;(3)、以点D为圆心,DA为半径作圆,⊙D与⊙M的公共弦恰好经过梯形的一个顶点,求此时⊙M的半径长.24. 如图,已知扇形AOB的半径OA=4,∠AOB=90°,点C、D分别在半径OA、OB上(点C不与点A重合),联结CD . 点P是弧AB上一点,PC=PD .
(1)、设CE= ,求证:四边形AMCD是平行四边形;(2)、联结EM , 设∠FMB=∠EMC , 求CE的长;(3)、以点D为圆心,DA为半径作圆,⊙D与⊙M的公共弦恰好经过梯形的一个顶点,求此时⊙M的半径长.24. 如图,已知扇形AOB的半径OA=4,∠AOB=90°,点C、D分别在半径OA、OB上(点C不与点A重合),联结CD . 点P是弧AB上一点,PC=PD . (1)、当cot∠ODC= ,以CD为半径的圆D与圆O相切时,求CD的长;(2)、当点D与点B重合,点P为弧AB的中点时,求∠OCD的度数;(3)、如果OC=2,且四边形ODPC是梯形,求 的值.25. 如图1,在矩形ABCD中,点E是边CD的中点,点F在边AD上,EF⊥BD , 垂足为G .
(1)、当cot∠ODC= ,以CD为半径的圆D与圆O相切时,求CD的长;(2)、当点D与点B重合,点P为弧AB的中点时,求∠OCD的度数;(3)、如果OC=2,且四边形ODPC是梯形,求 的值.25. 如图1,在矩形ABCD中,点E是边CD的中点,点F在边AD上,EF⊥BD , 垂足为G . (1)、如图2,当矩形ABCD为正方形时,求 的值;(2)、如果 = ,AF=x , AB=y , 求y与x的函数关系式,并写出函数定义域;(3)、如果AB=4cm,以点A为圆心,3cm长为半径的⊙A与以点B为圆心的⊙B外切.以点F为圆心的⊙F与⊙A、⊙B都内切.求 的值.26. 如图,⊙ 和⊙ 相交于A、B两点, 与AB交于点C, 的延长线交⊙ 于点D,点E为AD的中点,AE=AC,联结 .
(1)、如图2,当矩形ABCD为正方形时,求 的值;(2)、如果 = ,AF=x , AB=y , 求y与x的函数关系式,并写出函数定义域;(3)、如果AB=4cm,以点A为圆心,3cm长为半径的⊙A与以点B为圆心的⊙B外切.以点F为圆心的⊙F与⊙A、⊙B都内切.求 的值.26. 如图,⊙ 和⊙ 相交于A、B两点, 与AB交于点C, 的延长线交⊙ 于点D,点E为AD的中点,AE=AC,联结 . (1)、求证: ;(2)、如果 , ,求⊙ 的半径长.
(1)、求证: ;(2)、如果 , ,求⊙ 的半径长.

