备考2022年中考数学一轮复习专题:菱形
试卷更新日期:2022-01-13 类型:一轮复习
一、单选题
-
1. 菱形和矩形都具有的性质是( )A、四条边相等 B、四个角相等 C、对角线互相垂直 D、对角线互相平分2. 如图,在菱形ABCD中,E,F分别是AB,AC的中点,如果EF=2,那么菱形ABCD周长是( )
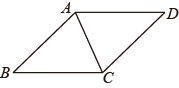
 A、4 B、8 C、12 D、163. 如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是( )
A、4 B、8 C、12 D、163. 如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是( ) A、AB= EF B、AB=2EF C、AB= EF D、AB= EF4. 如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节 间的距离,若 间的距离调节到60 ,菱形的边长 ,则 的度数是( )
A、AB= EF B、AB=2EF C、AB= EF D、AB= EF4. 如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节 间的距离,若 间的距离调节到60 ,菱形的边长 ,则 的度数是( ) A、 B、 C、 D、5. 菱形的周长是24,两邻角的度数之比是1:2,那么较短的对角线的长是( )A、3 B、5 C、6 D、6.56. 如图,在菱形ABCD中, , , 为等边三角形点E,F分别在菱形的边BC,CD上滑动,且E,F不与B,C,D重合,则四边形AECF的面积是( )
A、 B、 C、 D、5. 菱形的周长是24,两邻角的度数之比是1:2,那么较短的对角线的长是( )A、3 B、5 C、6 D、6.56. 如图,在菱形ABCD中, , , 为等边三角形点E,F分别在菱形的边BC,CD上滑动,且E,F不与B,C,D重合,则四边形AECF的面积是( ) A、4 B、 C、8 D、7. 如图,菱形 的对角线 , ,则该菱形的面积为( ).
A、4 B、 C、8 D、7. 如图,菱形 的对角线 , ,则该菱形的面积为( ). A、60 B、80 C、100 D、1208. 矩形具有而菱形不一定具有的性质是( )A、两组对边分别平行且相等 B、邻角互补 C、对角线相等 D、对角线互相垂直9. 如图,在菱形ABCD中,∠A=60°,AB=8cm,则菱形ABCD的面积是( )cm2
A、60 B、80 C、100 D、1208. 矩形具有而菱形不一定具有的性质是( )A、两组对边分别平行且相等 B、邻角互补 C、对角线相等 D、对角线互相垂直9. 如图,在菱形ABCD中,∠A=60°,AB=8cm,则菱形ABCD的面积是( )cm2 A、16 B、32 C、64 D、3210. 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=2,点D是AC边的中点,点E是AB边上一点,将△ADE沿直线DE折叠,得到△FDE,连接FC,EC.若四边形DECF是菱形,则BE的长为( )
A、16 B、32 C、64 D、3210. 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=2,点D是AC边的中点,点E是AB边上一点,将△ADE沿直线DE折叠,得到△FDE,连接FC,EC.若四边形DECF是菱形,则BE的长为( )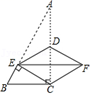 A、1 B、 C、2 D、4﹣
A、1 B、 C、2 D、4﹣二、填空题
-
11. 如图在菱形 中, 是对角线 上一动点过点 作 于 . 于点 .若菱形 的周长为 ,面积为 ,则 的值为 .
 12. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角度数,正方形ABCD变为菱形 ,若 ,且菱形 的面积为16,则正方形ABCD的面积为 .
12. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角度数,正方形ABCD变为菱形 ,若 ,且菱形 的面积为16,则正方形ABCD的面积为 .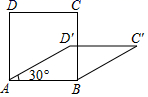 13. 如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是 .
13. 如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是 . 14. 如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=°.
14. 如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=°. 15. 如图,已知四边形ABCD是边长为4cm的菱形,∠BAD=60°,过点O的直线EF交AD于点E , 交BC于点F , 当∠EOD=30°时,CE的长是 .
15. 如图,已知四边形ABCD是边长为4cm的菱形,∠BAD=60°,过点O的直线EF交AD于点E , 交BC于点F , 当∠EOD=30°时,CE的长是 . 16. 在菱形ABCD中, , ,点P是射线BC上一动点,(不与B,C重合),连接PA,PD,当 是等腰三角形时,BP的长为 .
16. 在菱形ABCD中, , ,点P是射线BC上一动点,(不与B,C重合),连接PA,PD,当 是等腰三角形时,BP的长为 .三、综合题
-
17. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作 且 ,连接AE交OD于点F,连接OE
 (1)、求证: ;(2)、若菱形ABCD的边长为4, ,求AE的长.18. 在 中,AE平分 ,交BC于点E,BF平分 ,交AD于点F,AE与BF交于点O,连接EF、OC.
(1)、求证: ;(2)、若菱形ABCD的边长为4, ,求AE的长.18. 在 中,AE平分 ,交BC于点E,BF平分 ,交AD于点F,AE与BF交于点O,连接EF、OC. (1)、求证:四边形ABEF是菱形;(2)、若点E为BC的中点,且 , ,求OC的长.19. 如图,已知菱形ABCD,点E、F是对角线BD所在直线上的两点,且∠AED=45°,DF=BE,连接CE、AF、CF,得四边形AECF.
(1)、求证:四边形ABEF是菱形;(2)、若点E为BC的中点,且 , ,求OC的长.19. 如图,已知菱形ABCD,点E、F是对角线BD所在直线上的两点,且∠AED=45°,DF=BE,连接CE、AF、CF,得四边形AECF. (1)、求证四边形AECF是正方形;(2)、若BD=4,BE=3,求菱形ABCD的面积.20. 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)、求证四边形AECF是正方形;(2)、若BD=4,BE=3,求菱形ABCD的面积.20. 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F. (1)、证明:四边形ADCF是菱形;(2)、若AC=4,AB=5,求出菱形ADCF的面积.21. 如图,在平行四边形ABCD中,对角线AC与BD相交于O点,点E、F分别在OD、BO上,且OE=OF , 连接AE、CF .
(1)、证明:四边形ADCF是菱形;(2)、若AC=4,AB=5,求出菱形ADCF的面积.21. 如图,在平行四边形ABCD中,对角线AC与BD相交于O点,点E、F分别在OD、BO上,且OE=OF , 连接AE、CF . (1)、求证:△ADE≌△CBF .(2)、连接AF、CE , 当BD平分∠ABC时,四边形AFCE是什么特殊的四边形?请说明理由.22. 如图,在菱形ABCD中,对角线AC , BD交于点O , E是CD中点,连接OE . 过点C作CF BD交OE的延长线于点F , 连接DF .
(1)、求证:△ADE≌△CBF .(2)、连接AF、CE , 当BD平分∠ABC时,四边形AFCE是什么特殊的四边形?请说明理由.22. 如图,在菱形ABCD中,对角线AC , BD交于点O , E是CD中点,连接OE . 过点C作CF BD交OE的延长线于点F , 连接DF .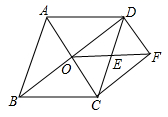 (1)、求证:四边形OCFD是矩形;(2)、若DF=2,CF=3,求菱形ABCD的面积.23. 如图,△ABC中,D是AB上一点,DE⊥AC于点E , F是AD的中点,FG⊥BC于点G , 与DE交于点H , 若FG=AF , AG平分∠CAB , 连接GE , GD .
(1)、求证:四边形OCFD是矩形;(2)、若DF=2,CF=3,求菱形ABCD的面积.23. 如图,△ABC中,D是AB上一点,DE⊥AC于点E , F是AD的中点,FG⊥BC于点G , 与DE交于点H , 若FG=AF , AG平分∠CAB , 连接GE , GD . (1)、求证:△ECG≌△GHD;(2)、当∠B为多少度时,四边形AEGF是否为菱形,请说明理由.24. 如图,在 中, ,D为 边上的一点以 为直径的 交 于点E,过点C作 ,垂足为G,交 于点F,过点E作 ,垂足为P, .
(1)、求证:△ECG≌△GHD;(2)、当∠B为多少度时,四边形AEGF是否为菱形,请说明理由.24. 如图,在 中, ,D为 边上的一点以 为直径的 交 于点E,过点C作 ,垂足为G,交 于点F,过点E作 ,垂足为P, .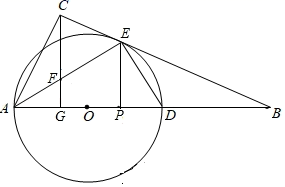 (1)、求证: 是 的切线;(2)、若 , , ,求四边形 的面积.25. 已知四边形ABCD是正方形,点P在线段BC上,点G在线段AD上(P、G不与正方形顶点重合,且在CD的同侧), , 于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF.
(1)、求证: 是 的切线;(2)、若 , , ,求四边形 的面积.25. 已知四边形ABCD是正方形,点P在线段BC上,点G在线段AD上(P、G不与正方形顶点重合,且在CD的同侧), , 于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF. (1)、求证: ;(2)、求证:四边形PEFD是菱形;(3)、若 , .求四边形PEFD的面积.26. (问题发现)数学小组成员小明做作业时遇到以下问题:
(1)、求证: ;(2)、求证:四边形PEFD是菱形;(3)、若 , .求四边形PEFD的面积.26. (问题发现)数学小组成员小明做作业时遇到以下问题:


图1 图2 图3
(1)、若四边形 是菱形, ,点 是射线 上一动点,以 为边向右侧作等边 ,如图1,当点E在菱形 内部或边上时,连接 ,则 与 有怎样的数量关系?请直接写出你的猜想;(2)、(类比探究)数学小组对该问题进行进一步探究:若四边形 是正方形,点P是射线 上一动点,以 为直角边在 边的右侧作等腰 ,其中 .
①如图2,当点 在对角线 上时,小组发现点 恰好在射线 上,求 与 之间的数量关系(过程只用说明点 在线段 上的情况即可);
②如图3,当P是对角线 的延长线上一动点时,小组发现点 恰好在射线 上,连接 ,若 ,求 的面积.
27. 如图,在平面直角坐标系xOy中,过点C的直线y=x+4与y=kx+4分别交x轴于点A,B.点E是AC的中点,点D的坐标是(﹣ ,0).连结OE交CD于F.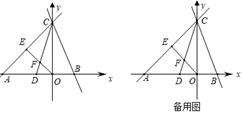 (1)、求点A,F的坐标;(2)、若∠ACD=∠OCB,求k的值;(3)、在(2)的条件下,过点F作直线l垂直于x轴,设点M在直线y=kx+4上,点N在x轴上,问:直线l上是否存在点H,使得以B,M,N,H为顶点的四边形是菱形?若存在,求出符合条件的点H的坐标;若不存在,说明理由.28. 如图,矩形 中, , ,点 是对角线 的中点,过点 的直线分别交 、 边于点 、 .
(1)、求点A,F的坐标;(2)、若∠ACD=∠OCB,求k的值;(3)、在(2)的条件下,过点F作直线l垂直于x轴,设点M在直线y=kx+4上,点N在x轴上,问:直线l上是否存在点H,使得以B,M,N,H为顶点的四边形是菱形?若存在,求出符合条件的点H的坐标;若不存在,说明理由.28. 如图,矩形 中, , ,点 是对角线 的中点,过点 的直线分别交 、 边于点 、 . (1)、求证:四边形 是平行四边形;(2)、当 时,求四边形 的面积.
(1)、求证:四边形 是平行四边形;(2)、当 时,求四边形 的面积.