备考2022年中考数学一轮复习专题：多边形和平行四边形

试卷更新日期：2022-01-13 类型：一轮复习

进入出卷网下载

一、单选题

1. 一个正多边形的外角与相邻的内角的度数之比为1：3，则这个多边形的边数是（）

A、8 B、9 C、6 D、5

查看试题解析
2. 如图，一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合，且与边AB、CD相交于G、H．将多边形OGBCH的面积记为S，三条线段GB、BC、CH的长度之和记为l，在大正六边形绕点O旋转过程中，下列说法正确的是（）．

A、S变化，l不变 B、S不变，l变化 C、S变化，l变化 D、S与l均不变

查看试题解析
3. 下列多边形中，内角和最大的是（）

A、 B、 C、 D、

查看试题解析
4. 正五边形的外角和是（）

A、 $180 °$ B、 $360 °$ C、 $540 °$ D、 $720 °$

查看试题解析
5. 如图，在△ABC中，点E、D、F分别在边AB、BC、CA上，且DE∥CA，DF∥BA．下列四个判断中，错误的是（）

A、四边形AEDF是平行四边形 B、如果∠BAC＝90°，那么四边形AEDF是矩形 C、如果AD平分∠BAC，那么四边形AEDF是菱形 D、如果AD⊥BC且BD＝CD，那么四边形AEDF是正方形

查看试题解析
6. 下列命题是真命题的是（）

A、对角线互相垂直平分的四边形是正方形 B、对角线相等的四边形是平行四边形 C、对角线互相垂直的四边形是菱形 D、对角线互相平分且相等的四边形是矩形

查看试题解析
7. 如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B运动，移动到点B停止，延长EO交CD于点F，则四边形AECF形状的变化依次为（）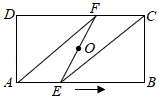

A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形

查看试题解析
8. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90^{°}$ ，以其三边为边向外作正方形，延长EA交BG于点M，连接IM交BC于点N，若M是BG的中点，则 $\frac{I N}{I M}$ 的值是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{1}{2}$

查看试题解析
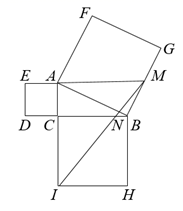9. 如图，直线l是五边形ABCDE的对称轴，其中 $∠ C = 100^{\circ}$ ， $∠ ABC = 130^{\circ}$ ，那么 $∠ BEA$ 的度数等于 $($ $)$

A、 $45^{\circ}$ B、 $50^{\circ}$ C、 $60^{\circ}$ D、 $65^{\circ}$

查看试题解析
10. 若一个多边形的每一个内角均为120°，则下列说法错误的是（）

A、这个多边形的内角和为720° B、这个多边形的边数为6 C、这个多边形是正多边形 D、这个多边形的外角和为360°

查看试题解析

二、填空题

11. 如图， $△ A B C$ 中，D为AC中点，E为BC上一点，连接DE，且 $∠ A B C = 2 ∠ D E C$ ，若 $A B = 7$ ， $C E = 12$ ，则BC的长度为．

查看试题解析
12. 在平面直角坐标系中，抛物线y=x²-3x+1的对称轴交x轴于点A，点B是位于x轴上方的对称轴上一点，BC∥x轴交对称轴右侧的抛物线于点C．若四边形OACB是平行四边形，则点C的坐标为．

查看试题解析
13. 七边形的内角和是

查看试题解析
14. 过 $n$ 边形的一个顶点的所有对角线，把 $n$ 边形分成了8个三角形，则这个多边形的边数是．

查看试题解析
15. 如图，菱形 $A B C D$ 的对角线 $A C ， B D$ 相交于点O，点E是边 $A B$ 的中点，若 $O E = 5.5$ ，则菱形 $A B C D$ 的周长为．

查看试题解析
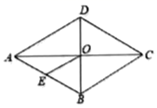16. 如图，矩形ABCD的边CD上有一点E， $∠ D A E = 22.5 °$ ， $E F ⊥ A B$ ，垂足为F，将 $△ A E F$ 绕着点F顺时针旋转，使得点A的对应点M落在EF上，点E恰好落在点B处，连接BE．下列结论：① $B M ⊥ A E$ ；②四边形EFBC是正方形；③ $∠ E B M = 30 °$ ；④ $A B = B E$ ，其中结论正确的为．（填写序号即可）

查看试题解析

三、综合题

17. 如图：在矩形ABCD中， $A B = 6 m$ ， $B C = 8 m$ ，动点Р以 $2 m / s$ 的速度从A点出发，沿AC向C点移动，同时动点Q以 $1 m / s$ 的速度从点C出发，沿CB向点B移动，设P、Q两点移动的时间为t秒 $(0 < t < 5)$ ．

(1)、 $A P =$ m， $P C =$ m， $C Q =$ m（用含t的代数式表示）

(2)、t为多少秒时，以P、Q、C为顶点的三角形与 $△ A B C$ 相似？

(3)、在P、Q两点移动过程中，四边形ABQP与 $△$ CPQ的面积能否相等？若能，求出此时t的值；若不能，请说明理由．

查看试题解析
18. 如图，矩形 $O A B C$ 的顶点A，C分别落在x轴，y轴的正半轴上，顶点 $B (2 ， 2 \sqrt{3})$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与 $B C$ ， $A B$ 分别交于D，E， $B D = \frac{1}{2}$ ．

(1)、求反比例函数关系式和点E的坐标；

(2)、写出 $D E$ 与 $A C$ 的位置关系并说明理由；

(3)、点F在直线 $A C$ 上，点G是坐标系内点，当四边形 $B C F G$ 为菱形时，求出点G的坐标．

查看试题解析
19. 已知，点D是 $△ A B C$ 的边AB上一点，点M为AC的中点，过点C作 $C N ∥ A B$ 交DM的延长线于N，连接CD、AN．

(1)、如图1，求证：四边形ADCN是平行四边形；

(2)、如图2，若 $∠ A M D = 2 ∠ M C D$ ， $∠ A C B = 90 °$ ， $A C = B C$ ，请直接写出图中所有与线段AN相等的线段（线段AN除外）．

查看试题解析
20. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ 点D是边AB上的一个动点，连接CD．作 $A E ∥ D C$ ， $C E ∥ A B$ ，连接ED．

(1)、如图1，当 $C D ⊥ A B$ 时，求证： $A C = E D$ ；

(2)、如图2，当D是AB的中点时，
①四边形ADCE的形状是 ▲ ；请说明理由．

②若 $A B = 5$ ， $E D = 4$ ，则四边形ADCE的面积为 ▲ ．

查看试题解析
21. 综合与探究
如图，在平面直角坐标系中，点 $A (0 ， 10)$ ，点B是x轴的正半轴上的一个动点，连接AB，取AB的中点M，将线段MB绕着点B按顺时针方向旋转90°，得到线段BC．过点B作x轴的垂线交直线AC于点D．设点B坐标是 $(t ， 0)$

(1)、当 $t = 6$ 时，点M的坐标是；

(2)、用含t的代数式表示点C的坐标；

(3)、是否存在点B，使四边形AOBD为矩形？若存在，请求出点B的坐标；若不存在，请说明理由；

(4)、在点B的运动过程中，平面内是否存在一点N，使得以A、B、N、D为顶点的四边形是菱形？若存在，请直接写出点N的纵坐标（不必要写横坐标）；若不存在，请说明理由．

查看试题解析
22. 如图，四边形ABCD中，AD//BC， $∠ A D C = 90^{°}$ ， $A D = 8$ ， $B C = C D = 6$ ，点M从点D出发，以每秒2个单位长度的速度向点A运动，同时，点N从点B出发，以每秒1个单位长度的速度向点C运动．当其中一个动点到达终点时，另一个动点也随之停止运动．过点N作 $N P ⊥ A D$ 于点P，连接AC交NP于点Q，连接MQ，设运动时间为t秒（ $0 < t < 4$ ）

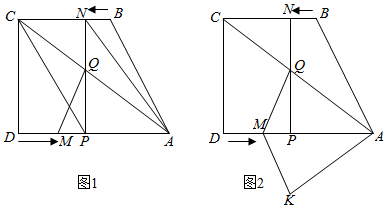(1)、连接AN，CP，当t为何值时，四边形ANCP为平行四边形；

(2)、设四边形DMQC的面积为y，求y与t的函数关系式；

(3)、在运动过程中，是否存在某一时刻t，使四边形DMQC的面积与△ABC的面积相等？若存在，求出t的值；若不存在，请说明理由；

(4)、将△AQM沿AD翻折，得到△AKM．在运动过程中，是否存在某时刻t，使四边形AQMK为菱形，若存在，求出t的值；若不存在，请说明理由．

查看试题解析
23. 已知：如图，在▱ABCD中，点E是BC的中点，连接AE并延长交DC的延长线于点F，连接BF．

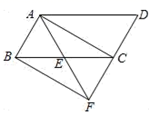(1)、求证：△ABE≌△FCE；

(2)、若AF＝AD，判断四边形ABFC的形状，并说明理由．

查看试题解析
24. 如图，在平行四边形ABCD中，对角线AC、BD相交于点O，以AC为斜边的等腰直角三角形AEC的边CE与AD交于点F，连接OE，使得 $O E = O D$ ．在AD上截取 $A H = C D$ ，连接EH、ED．

(1)、判断四边形ABCD的形状，并说明理由；

(2)、若 $A B = 2$ ， $B C = 6$ ，求EH的长．

查看试题解析
25. 已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．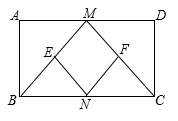

(1)、求证： $△ A B M ≌ △ D C M$ ；

(2)、判断四边形MENF是什么特殊四边形，并证明你的结论；

(3)、当AD，AB满足什么条件时，四边形MENF是正方形．

查看试题解析
26. 已知：平行四边形ABCD的两边AB、BC的长是关于x的方程 $x^{2} - (m + 3) x + 2 m + 2 = 0$ 的两个实数根．

(1)、试说明：无论m取何值方程总有两个实数根

(2)、当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；

(3)、若AB的长为3，那么平行四边形ABCD的周长是多少？

查看试题解析
27. 如图1，已知在Rt△ABC中，AB＝5cm，BC＝12cm，以BC为边作正方形BCDE ，点P从点A出发，沿ABE方向匀速运动，速度为1cm/s；同时，点Q从点C出发，沿CA方向匀速运动，速度为2cm/s，连接PQ ．设运动时间为t（s）（0＜t＜6.5），解答下列问题：

(1)、当t为何值时，PQ∥BC？

(2)、如图2，连接PQ ，交BC于点F ，是否存在某一时刻t ，使△BFP与△QFC相似？

(3)、用含t的代数式表示出五边形PEDCQ的面积．

查看试题解析
28. 综合与实践
如图1，已知点G在正方形ABCD的对角线AC 上，GE⊥BC，垂足为E，GF⊥CD，垂足为F．

(1)、（证明与推断）
①四边形CEGF的形状是；

② $\frac{A G}{B E}$ 的值为；

(2)、（探究与证明）
在图1的基础上，将正方形CEGF绕点C按顺时针方向旋转α角（0°<α<45°），如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；

(3)、（拓展与运用）
如图3，在（2）的条件下，正方形CEGF 在旋转过程中，当B、E、F三点共线时，探究AG和GE的位置关系，并说明理由．

查看试题解析