备考2022年中考数学一轮复习专题：等腰三角形

试卷更新日期：2022-01-13 类型：一轮复习

进入 出卷网 下载

一、单选题

  • 1. 如图所示，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则最小值为（ ）

    A、2 B、3 C、4 D、6

    查看试题解析

  • 2. 如图，在正五边形ABCDE中，连接AD ， 则∠DAE的度数为（    ）

    A、46° B、56° C、36° D、26°

    查看试题解析

  • 3. 已知三角形三个内角的度数之比为3：3：4，则这个三角形是（    ）
    A、等腰三角形 B、直角三角形 C、钝角三角形 D、等边三角形

    查看试题解析

  • 4. 如图， △ABC 是等边三角形，D是线段 AC 上一点（不与点A，C重合），连接 BD ，点E，F分别在线段 BA ， BC 的延长线上，且 DE=DF=BD ，则 △AED 的周长等于（    ）

    A、AB+AE B、BC+CF C、2AC D、AC+BD

    查看试题解析

  • 5. 如图，点D为等边 ΔABC 内部一个动点，运动过程中始终满足 DB=DA ，点C关于 BD 的对称点为点F，连接 BF ， DF ，则 ∠BFD 的度数为（    ）

    A、30° B、20° C、15° D、不确定

    查看试题解析

  • 6. 如图，正方形的网格中，点A ， B是小正方形的顶点，如果C点是小正方形的顶点，且使△ABC是等腰三角形，则点C的个数为（    ）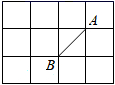

    A、6 B、7 C、8 D、9

    查看试题解析

  • 7. 等腰三角形一腰上的高与另一腰的夹角为20°，则其底角的大小为（　　）
    A、65° B、105° C、55°或35° D、65°或115°

    查看试题解析

  • 8. 等腰三角形的一个底角等于 55° ，则它的顶角等于（    ）
    A、45° B、55° C、70° D、80°

    查看试题解析

  • 9. 已知等腰三角形一腰上的高线与另一腰的夹角为 40° ，那么这个等腰三角形的顶角等于（    ）．
    A、50° 或 130° B、130° C、80° D、50° 或 80°

    查看试题解析

  • 10. 如图，在等边 △ ABC中，AD是它的角平分线，DE⊥AB于E，若AC=8，则BE=（    ）

    A、1 B、2 C、3 D、4

    查看试题解析

二、填空题

  • 11. 如图，在等边三角形ABC中，CD⊥AB于点D，若AB=2，则CD的长是 ．

    查看试题解析

  • 12. 如图， △ABC 中，D为AC中点，E为BC上一点，连接DE，且 ∠ABC=2∠DEC ，若 AB=7 ， CE=12 ，则BC的长度为 ．

    查看试题解析

  • 13. 如图， △ABC 中， AB=AC ， ∠BAC=36° ，以点C为圆心， CB 长为半径画弧，交 AB 于点B和点D．若 BC=1 ，则 AD 的长度是 ．

    查看试题解析

  • 14. 如图，已知点P是射线ON上一动点（即P可在射线ON上运动），∠AON=45°，当∠A=时，△AOP为等腰三角形．

    查看试题解析

  • 15. 如图，△ABC是等边三角形，AD⊥BC于点D ， AE＝AD ， 则∠ADE的度数为 ．

    查看试题解析

  • 16. 等腰三角形的一边长为4cm，周长为14cm，则该三角形的底边长为 ．

    查看试题解析

三、综合题

  • 17. 如图， △ABC 为等边三角形，点D为 BC 延长线上的一点， CE 平分 ∠ACD ，且 CE=BD ，连接 AD ， AE ， DE ．

    (1)、求证： AB∥CE ；
    (2)、试判断 △ADE 的形状，并说明理由．

    查看试题解析

  • 18. 如图，△ABC是等边三角形，点D、E分别在边BC、AC上，AE＝CD ， AD与BE相交于点F ， BG⊥AD ， 垂足为G ．

    (1)、求证：△ABE≌△CAD；
    (2)、若FG＝3，EF＝1，求AD的长．

    查看试题解析

  • 19. 如图，在四边形ABCD中，∠ABC＝90°，AD // BC，AB＝BC．E是AB中点，CE⊥BD．

    (1)、求证：AD＝BE．
    (2)、求证：AC⊥DE．
    (3)、△ DBC是等腰三角形吗？说明理由．

    查看试题解析

  • 20. 如图，在 △ABC 中， AB=AC ，M，N分别是 AB ， AC 边上的点，并且 MN∥BC ．

    (1)、求证： △AMN 是等腰三角形；
    (2)、点P是 MN 上的一点，并且 BP 平分 ∠ABC ，求证： △BPM 是等腰三角形；

    查看试题解析

  • 21. 如图，在等边 △ABC 中，点D是边 AB 上一点，E是 BC 延长线上一点， CE=DA ，连接 DE 交 AC 于点F，过点D作 DG⊥AC 于点G，过点D作 DH∥BC 交 AC 于点H．

    (1)、求证： AG=12AD ；
    (2)、求证： DF=EF ；
    (3)、若 CF=CE ， S△ADG=2 ，求出 △DGF 的面积．

    查看试题解析

  • 22. △ABC 与 △CDE 都是等边三角形，连接AD、BE．

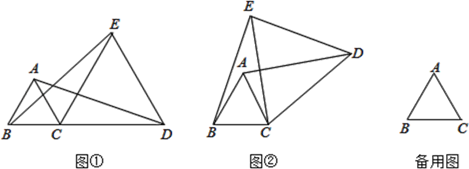    (1)、如图①，当点B、C、D在同一条直线上时，则 ∠BCE= 度；
    (2)、将图①中的 △CDE 绕着点C逆时针旋转到如图②的位置，求证： AD=BE ．

    查看试题解析

  • 23. 我们经常遇到需要分类的问题，画“树形图”可以帮我们不重复、不遗漏地分类．

    （问题提出）

    (1)、在等腰三角形ABC中，若∠A＝80°，根据下面分析、直接写出∠B的度数 ．

    分析：∠A、∠B都可能是顶角或底角，因此需要分成如图所示的3类，这样的图就是树形图．请根据此分析、求出∠B的度数．

    (2)、（问题解决）

    已知等腰三角形ABC周长为19，AB＝7，仿照例题画出树形图，并求出BC的长度．

    查看试题解析

  • 24. 如图， P 为等边三角形 ΔABC 内一点，分别连接 PA ， PB ， PC ， PA=6 ， PB=8 ， PC=10 ．以 PA 为边作等边三角形 ΔAPD ，连接 BD ．

    (1)、求证： BD=PC ．
    (2)、求 ∠APB 的度数．

    查看试题解析

  • 25. 如图，在等边△ABC中，AB＝9cm，点P从点C出发沿CB边向点B以2cm/s的速度移动，点Q从B点出发沿BA边向A点以5cm/s速度移动．Q两点同时出发，它们移动的时间为t秒钟．

    (1)、你能用t表示BP和BQ的长度吗？请你表示出来．
    (2)、请问几秒钟后，△PBQ为等边三角形？
    (3)、若P、Q两点分别从C ． B两点同时出发，并且都按顺时针方向沿AEC三边运动，请问经过几秒钟后点P与点Q第一次在△ABC的哪条边上相遇？．

    查看试题解析

  • 26. 如图，等边△ABC中，A ， B关于y轴对称，AD⊥AC交y轴负半轴于点D ， C（0，6）．

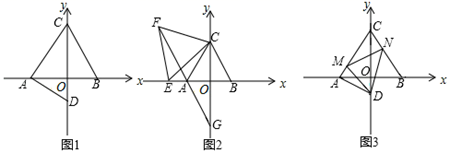    (1)、如图1，求D点坐标；
    (2)、如图2，E为x轴负半轴上任一点，以CE为边作等边△CEF ， FA的延长线交y轴于点G ， 求OG的长；
    (3)、如图3，在（1）的条件下，以D为顶点作60°的角，它的两边分别与CA、BC交于点MN ， 连接MN ． 探究线段AM、MN、NB之间的关系，并予以证明．

    查看试题解析

  • 27. 在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED＝EC ．

    (1)、当点E为AB的中点时，如图1，确定线段A与DB的大小关系，请你直接写出结论：AEDB（填“＞”，“＜”或“＝”）．
    (2)、当E不是AB的中点时，AE与DB的大小关系是：AEDB（填“＞”，“＜”或“＝”）．理由如下：如图2，过点E作EF∥BC ， 交AC点F ． 请你接下来按照这种思路完成全部解答过程．
    (3)、在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED＝EC ． 若△ABC的边长为2，AE＝4，则CD的长为 ．

    查看试题解析

  • 28. 如图，在△ABC中，AB＝AC ， 点D、E、F分别在AB、BC、AC边上，且BE＝CF ， BD＝CE ．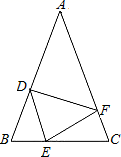

    (1)、求证：△DEF是等腰三角形；
    (2)、当∠A＝40°时，求∠DEF的度数．

    查看试题解析