备考2022年中考数学一轮复习专题:角平分线与线段垂直平分线
试卷更新日期:2022-01-13 类型:一轮复习
一、单选题
-
1. 如图 ABC≌ ,边 过点A且平分∠BAC交BC于点D , ∠B=26°, =94°,则 的度数为( )
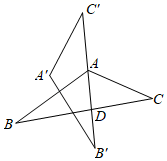 A、34° B、40° C、45° D、60°2. 如图,在 ABC中,AD平分∠BAC , ,AB=7cm,BD=3cm,则 BDE的周长为( )
A、34° B、40° C、45° D、60°2. 如图,在 ABC中,AD平分∠BAC , ,AB=7cm,BD=3cm,则 BDE的周长为( )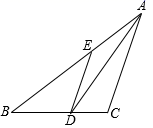 A、13cm B、10cm C、4cm D、7cm3. 如图,在 ABC中,∠ABC的平分线BP与AC的垂直平分线DP相交于点P , 过点P作PF⊥BC于点F , PE⊥AB交BA的延长线于点E . AB=7cm,BC=15cm,则AE的长为( )
A、13cm B、10cm C、4cm D、7cm3. 如图,在 ABC中,∠ABC的平分线BP与AC的垂直平分线DP相交于点P , 过点P作PF⊥BC于点F , PE⊥AB交BA的延长线于点E . AB=7cm,BC=15cm,则AE的长为( ) A、3cm B、4cm C、5cm D、6cm4. 如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E. F,分别以E. F为圆心,以大于 EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法错误的是( )
A、3cm B、4cm C、5cm D、6cm4. 如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E. F,分别以E. F为圆心,以大于 EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法错误的是( ) A、∠ADB=∠ABC B、AB=BD C、AC=AD+BD D、∠ABD=∠BCD5. 如图,AD是△ABC的角平分线,DE⊥AB于点E , S△ABC=10,DE=2,AB=4, 则AC长是( )
A、∠ADB=∠ABC B、AB=BD C、AC=AD+BD D、∠ABD=∠BCD5. 如图,AD是△ABC的角平分线,DE⊥AB于点E , S△ABC=10,DE=2,AB=4, 则AC长是( ) A、9 B、8 C、7 D、66. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ).
A、9 B、8 C、7 D、66. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ). A、在 AC、BC 两边高线的交点处 B、在 AC、BC 两边垂直平分线的交点处 C、在 AC、BC 两边中线的交点处 D、在∠A、∠B两内角平分线的交点处7. 如图,在 的斜边 上截取 ,过点D作 交 于点E。若点E恰好为 的中点,则下列结论中错误的是( )
A、在 AC、BC 两边高线的交点处 B、在 AC、BC 两边垂直平分线的交点处 C、在 AC、BC 两边中线的交点处 D、在∠A、∠B两内角平分线的交点处7. 如图,在 的斜边 上截取 ,过点D作 交 于点E。若点E恰好为 的中点,则下列结论中错误的是( ) A、 B、 C、 D、8. 如图,△ABC中,DE是AB的垂直平分线,△ABC的周长为19cm,△ADC的周长为13cm,则AE的长为( )
A、 B、 C、 D、8. 如图,△ABC中,DE是AB的垂直平分线,△ABC的周长为19cm,△ADC的周长为13cm,则AE的长为( ) A、3cm B、4cm C、6cm D、8cm9. 如图,在△ABC中,∠B=70°,∠C=25°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于M , N , 作直线MN , 交BC于D , 连接AD , 则∠BAD的度数是( )
A、3cm B、4cm C、6cm D、8cm9. 如图,在△ABC中,∠B=70°,∠C=25°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于M , N , 作直线MN , 交BC于D , 连接AD , 则∠BAD的度数是( ) A、50° B、60° C、65° D、75°10. 如图,在 中, 是 的垂直平分线, , 的周长为 ,则 的周长是( ).
A、50° B、60° C、65° D、75°10. 如图,在 中, 是 的垂直平分线, , 的周长为 ,则 的周长是( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在 中, ,边 的垂直平分线 交 于点D, 平分 ,则 .
 12. 如图,AD平分∠BAC , DE AB , DF⊥AB . 若AE=8,∠BAC=30°,则DF的长为 .
12. 如图,AD平分∠BAC , DE AB , DF⊥AB . 若AE=8,∠BAC=30°,则DF的长为 .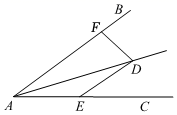 13. 如图,点D在△ABC边BC的延长线上,CE平分∠ACD , ∠A=80°,∠B=30°,则∠ACE的大小为 .
13. 如图,点D在△ABC边BC的延长线上,CE平分∠ACD , ∠A=80°,∠B=30°,则∠ACE的大小为 . 14. 如图,等腰△ABC中,AB=AC=7,BC=6,AB的垂直平分线MN交AC于点D,则△BDC的周长是 .
14. 如图,等腰△ABC中,AB=AC=7,BC=6,AB的垂直平分线MN交AC于点D,则△BDC的周长是 . 15. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是 .
15. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是 .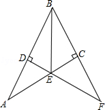 16. 如图,在△ABC中,AB和AC的垂直平分线分别交BC于E、F,若∠BAC=130°,则∠EAF= .
16. 如图,在△ABC中,AB和AC的垂直平分线分别交BC于E、F,若∠BAC=130°,则∠EAF= .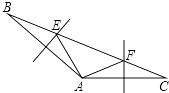
三、综合题
-
17. 如图,在△ABC中,D , E分别是BC和AB上的点,AD、CE相交于F .
 (1)、若AD , CE分别平分∠BAC和∠ACB , 已知∠B=40°,求∠AFE的度数;(2)、设BC=a , AC=b , AB=c , 若△ABD与△ACD的周长相等,△CAE与△CBE的周长相等,求AE和BD的长.(用含a、b、c的式子表示)18. 中, 平分 交 于点 ,从点 作 交 的延长线于点 .
(1)、若AD , CE分别平分∠BAC和∠ACB , 已知∠B=40°,求∠AFE的度数;(2)、设BC=a , AC=b , AB=c , 若△ABD与△ACD的周长相等,△CAE与△CBE的周长相等,求AE和BD的长.(用含a、b、c的式子表示)18. 中, 平分 交 于点 ,从点 作 交 的延长线于点 .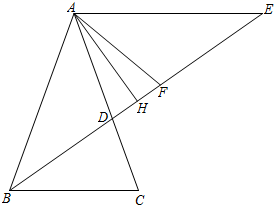 (1)、若 ,求 的度数;(2)、点 是 上一点,且 .取 的中点 ,请问 吗?试说明理由.19.
(1)、若 ,求 的度数;(2)、点 是 上一点,且 .取 的中点 ,请问 吗?试说明理由.19. (1)、我们已经知道,在 中,如果 ,则 ,下面我们继续研究:如图①,在 中,如果 ,则 与 的大小关系如何?为此,我们把 沿 的平分线翻折,因为 ,所以点 落在 边的点 处,如图②所示,然后把纸展平,连接 ,接下来,你能推出 与 的大小关系了吗?试写出说理过程.(2)、如图③,在 中, 是角平分线,且 ,求证: .(3)、在(2)的条件下,若点 、 分别为 、 上的动点,且 , ,则 的最小值为.20. 在四边形ABCD中,∠A=∠C=90°.
(1)、我们已经知道,在 中,如果 ,则 ,下面我们继续研究:如图①,在 中,如果 ,则 与 的大小关系如何?为此,我们把 沿 的平分线翻折,因为 ,所以点 落在 边的点 处,如图②所示,然后把纸展平,连接 ,接下来,你能推出 与 的大小关系了吗?试写出说理过程.(2)、如图③,在 中, 是角平分线,且 ,求证: .(3)、在(2)的条件下,若点 、 分别为 、 上的动点,且 , ,则 的最小值为.20. 在四边形ABCD中,∠A=∠C=90°.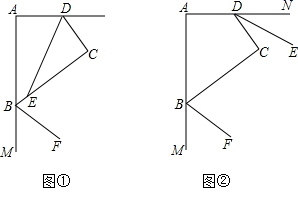 (1)、求:∠ABC+∠ADC=°;(2)、如图①,若DE平分∠ADC , BF平分∠CBM , 写出DE与BF的位置关系.(3)、如图②,若BF , DE分别平分∠ABC , ∠ADC的外角,写出BF与DE的位置关系,对(2)和(3)任选一个加以证明.21. 如图,AD为△ABC的中线,BE为△ABD的中线.
(1)、求:∠ABC+∠ADC=°;(2)、如图①,若DE平分∠ADC , BF平分∠CBM , 写出DE与BF的位置关系.(3)、如图②,若BF , DE分别平分∠ABC , ∠ADC的外角,写出BF与DE的位置关系,对(2)和(3)任选一个加以证明.21. 如图,AD为△ABC的中线,BE为△ABD的中线. (1)、∠ABE=15°,∠BAD=40°,求∠BED的度数;(2)、尺规作图:过点E作EF⊥BC , 垂足为F(保留作图痕迹);(3)、在(2)的条件下,若△ABC的面积为40,BC=10,求EF的长.22.
(1)、∠ABE=15°,∠BAD=40°,求∠BED的度数;(2)、尺规作图:过点E作EF⊥BC , 垂足为F(保留作图痕迹);(3)、在(2)的条件下,若△ABC的面积为40,BC=10,求EF的长.22. (1)、[证明体验]
(1)、[证明体验]如图13-1,AD为△ABC的角平分线,∠ADC=60°,点E在AB上,AE=AC.求证:DE平分∠ADB.
(2)、[思考探究]如图13-2,在(1)的条件下,F为AB上一点,连结FC交AD于点G.若FB=FC,DG=2,CD=3,求BD的长.
(3)、[拓展延伸]如图13-3,在四边形ABCD中,对角线AC平分∠BAD,∠BCA=2∠DCA,点E在AC上,∠EDC=∠ABC.若BC=5,CD=2 ,AD=2AE,求AC的长.
23. 如图,在△ABC中,AB=AC , DE垂直平分AB , 交边AB于点D , 交边AC于点E , BF垂直平分CE , 交AC于点F , 连接BE . (1)、求证:AE=BC;(2)、求∠A的度数.24. 尺规作图,如图,已知三角形△ABC .
(1)、求证:AE=BC;(2)、求∠A的度数.24. 尺规作图,如图,已知三角形△ABC . (1)、尺规作图,作BC的垂直平分线DE , 分别交AB于D、交BC于E(不要求写作法,保留作图痕迹)(2)、连结CD , 若BE=5,△ACD的周长为12,求△ABC的周长.25. 如图1所示,在 中, , 的垂直平分线交 于点 ,交 或 的延长线于点 .
(1)、尺规作图,作BC的垂直平分线DE , 分别交AB于D、交BC于E(不要求写作法,保留作图痕迹)(2)、连结CD , 若BE=5,△ACD的周长为12,求△ABC的周长.25. 如图1所示,在 中, , 的垂直平分线交 于点 ,交 或 的延长线于点 . (1)、如图1所示,若 ,求 的大小;(2)、如图2所示,如果将(1)中的 的度数改为 ,其余条件不变,再求 的大小;(3)、你发现了什么规律?写出猜想,并说明理由.26. 如图,在 中,已知 , 的垂直平分线交 于点D , 交 于点E , 连接 .
(1)、如图1所示,若 ,求 的大小;(2)、如图2所示,如果将(1)中的 的度数改为 ,其余条件不变,再求 的大小;(3)、你发现了什么规律?写出猜想,并说明理由.26. 如图,在 中,已知 , 的垂直平分线交 于点D , 交 于点E , 连接 . (1)、若 ,求 的度数;(2)、若点P为直线 上一点, ,求 周长的最小值.27. 如图,在 中, 边的垂直平分线 交 于点 , 边的垂直平分线 交 于点 , 与 相交于点 ,连结 , , ,若 的周长为 , 的周长为 .
(1)、若 ,求 的度数;(2)、若点P为直线 上一点, ,求 周长的最小值.27. 如图,在 中, 边的垂直平分线 交 于点 , 边的垂直平分线 交 于点 , 与 相交于点 ,连结 , , ,若 的周长为 , 的周长为 . (1)、求线段 的长;(2)、求线段 的长.28. 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,DE⊥AB交BC于点E,CD交AE于点F.
(1)、求线段 的长;(2)、求线段 的长.28. 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,DE⊥AB交BC于点E,CD交AE于点F.
 (1)、求证:△AEB∽△CDB.(2)、若AE⊥CD,求AC:BC的值.(3)、若DF=2EF=4,求AF的值.29. 下面是小明解决一道课本练习题的过程及反思,请认真阅读并完成相应学习任务.
(1)、求证:△AEB∽△CDB.(2)、若AE⊥CD,求AC:BC的值.(3)、若DF=2EF=4,求AF的值.29. 下面是小明解决一道课本练习题的过程及反思,请认真阅读并完成相应学习任务.一道课后练习题的解答与思考:如图,要测量池塘两岸相対两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长.为什么?

理由如下:∵AB⊥BD,ED⊥BD,
∴∠ABC=∠EDC=90°.
∴在 ABC和 EDC中,
∴ ABC≌ EDC(依据1)
∵AB=ED(依据2)
∴测得DE的长就是AB的长.
反思:由于本题中AB ED,且C为BD的中点,因而可以用全等三角形的有关知识把AB的长度转化为DE的长度.所以当我们遇到“平行线和中点”的有关问题时,常常可以构造“X”型全等三角形解决问题,达到转化线段或角的目的.
(1)、任务一:上述材料中的依据1,依据2分别指的是什么?①依据1:;
②依据2: .
(2)、任务二:如图,四边形ABCD中,AD BC,点E是CD的中点,AE⊥BE.求证:AB=AD+BC.