浙教版备考2022年中考数学一轮复习专题12 函数基础知识

试卷更新日期：2022-01-13 类型：一轮复习

进入出卷网下载

一、单选题

1. 2021年春节期间，疫情形势复杂，王丽遵循“防疫当前，本地过年”的原则，给远在家乡的家人打电话拜年．电话费随着时间的变化而变化，在这个过程中，因变量是（）

A、王丽 B、电话费 C、时间 D、家人

查看试题解析
2. 函数 $y = \frac{\sqrt{x}}{x - 1}$ 的自变量取值范围是（）

A、 $x \neq 1$ B、 $x \geq 0$ C、 $x > 0$ D、 $x \geq 0$ 且 $x \neq 1$

查看试题解析
3. 甲、乙两人沿同一条路从A地出发，去往100千米外的B地，甲、乙两人离A地的距离（千米）与时间t（小时）之间的关系如图所示，以下说法正确的是（）

A、甲的速度是 $60km/h$ B、乙的速度是 $30km/h$ C、乙同时到达 D、甲出发两小时后两人第一次相遇

查看试题解析
4. 下列图象中，表示y是x的函数的个数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 已知A ， B两地相距60km，甲从A地去B地，乙从B地去A地，图中l₁ ， l₂分别表示甲、乙两人离B地的距离y（km）与甲出发时间x（h）的函数关系图象．设两人相遇在P处，则PA的距离为（　　）

A、42km B、28km C、24km D、18km

查看试题解析
6. 如图，正方形ABCD中，AB=8cm，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，到点C，D时停止运动，设运动时间为t（s），△OEF的面积为s（cm²），则s（cm²）与t（s）的函数关系可用图象表示为（）

A、 B、 C、 D、

查看试题解析
7. 如图1，四边形ABCD中， $A B / / C D$ ， $∠ B = 90 °$ ， $A C = A D$ ．动点Р从点B出发，沿折线 $B - A - D - C$ 方向以 $a$ 单位/秒的速度匀速运动，在整个运动过程中， $△ B C P$ 的面积S与运动时间t（秒）的函数图象如图2所示，则四边形ABCD的面积是（）

A、75 B、80 C、85 D、90

查看试题解析
8. 习近平总书记在全国教育大会上强调，要坚持中国特色社会主义教育发展道路．培养德智体美劳全面发展的社会主义建设者和接班人．枣庄某学校利用周未开展课外劳动实践活动．如图反映的过程是：小强从家去菜地浇水，又去玉米地除草，然后回家．如果菜地和玉米地的距离为a千米，小强在玉米地除草比在菜地浇水多用的时间为b分钟，则a ， b的值分别为（）

A、1.1，8 B、0.9，3 C、1.1，12 D、0.9，8

查看试题解析
9. 如图，矩形纸片ABCD中，BC=4，AB=3，点P是BC边上的动点（点P不与点B、C重合）．现将△PCD沿PD翻折，得到△PC′D ，作∠BPC′的角平分线，交AB于点E ．设BP=x ， BE=y ，则下列图象中，能表示y与x的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 如图，直线l为抛物线 $y = - x^{2} + 2 x + 3$ 的对称轴，点P为抛物线上一动点（在顶点或顶点的右侧），过点P作 $P A ⊥ x$ 轴于点A ，作PB∥x轴交抛物线于点B ，设 $P A = h$ ， $P B = m$ ，则h与m的函数图象大致为（）

A、 B、 C、 D、

查看试题解析
11. 小明根据某个一次函数关系式填写了如下的表格：其中有一格不慎被墨汁遮住了，想想看，该空格里原来填的数是（）

$x$

－2

-1

0

1

$y$

6

2

0

A、－2 B、0 C、2 D、4

查看试题解析
12. 如图，有一个球形容器，小海在往容器里注水的过程中发现，水面的高度h、水面的面积S及注水量V是三个变量．下列有四种说法：①S是V的函数；②V是S的函数；③h是S的函数；④S是h的函数．其中所有正确结论的序号是（）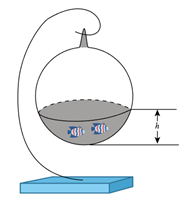

A、①③ B、①④ C、②③ D、②④

查看试题解析

二、填空题

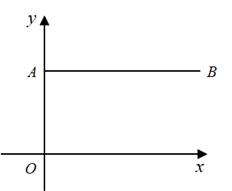
13. 如图，在平面直角坐标系中，点A的坐标为（0，3），点B的坐标为（6，3）．若抛物线y＝mx²＋2mx＋m＋3（m为常数，m≠0）向右平移a（a＞0）个单位长度，平移后的抛物线的顶点在线段AB上，则a的取值范围为．

查看试题解析
14. 甲、乙两人在一条笔直的道路上相向而行，甲骑自行车从A地到B地，乙驾车从B地到A地，他们分别以不同的速度匀速行驶，已知甲先出发6分钟后，乙才出发，在整个过程中，甲、乙两人的距离y（千米）与甲出发的时间x（分）之间的关系如图所示，当乙到达终点A时，甲还需分钟到达终点B．

查看试题解析
15. 小亮从学校步行回家，图中的折线反映了小亮离家的距离S（米）与时间t（分钟）的函数关系，根据图象提供的信息，给出以下结论：①他在前12分钟的平均速度是70米/分钟；②他在第19分钟到家；③他在第15分钟离家的距离和第24分钟离家的距离相等；④他在第33分钟离家的距离是720米．其中正确的序号为．

查看试题解析
16. 笔直的海岸线上依次有A ， B ， C三个港口，甲船从A港口出发，沿海岸线匀速驶向C港口，1小时后乙船从B港口出发，沿海岸线匀速驶向A港口，两船同时到达目的地．甲船的速度是乙船的1.25倍，甲、乙两船与B港口的距离 $y (km)$ 与甲船行驶时间 $x (h)$ 之间的函数关系如图所示．给出下列说法：①A ， B港口相距 $400 km$ ；②乙船的速度为 $80 km / h$ ；③B ， C港口相距 $200 km$ ；④乙船出发 $4 h$ 时，两船相距 $220 km$ ．其中正确的是（填序号）．

查看试题解析
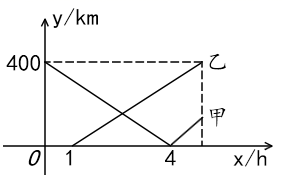17. 下面是王刚和李明两位同学的行程图，如果两人同时在同一地点出发，沿着200米的环形跑道同向行走，那么分钟后两人首次相遇．

查看试题解析
18. 一辆轿车和一辆货车分别从甲、乙两地同时出发，匀速相向而行，相遇后继续前行，已知轿车比货车每小时多行驶10千米，设行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系．根据图象提供的信息，下列说法正确的是．
①甲乙两地的距离为450千米

②点A的实际意义是两车出发2小时相距150千米

③x＝3时，两车相遇

④货车的速度为90千米/小时

查看试题解析

三、综合题

19. 甲、乙两人分别从同一公路上的A ， B两地同时出发骑车前往C地，两人行驶的路程y（km）与甲行驶的时间x（h）之间的关系如图所示，请根据图象所提供的信息解答下列问题：

(1)、A ， B两地相距 km；乙骑车的速度是 km/h；

(2)、请分别求出甲、乙两人在0≤x≤6的时间段内y与x之间的函数关系式；

(3)、求甲追上乙时用了多长时间．

查看试题解析
20. 一次函数 $y = k x + 3$ 的图象经过点 $(- 3 ， 9)$ ．

(1)、求这个函数的解析式；

(2)、试判断点 $(\frac{5}{4} ， - 4)$ 与点 $(- \frac{5}{6} ， \frac{14}{3})$ 是否在这个函数的图象上；

(3)、在如图所示的平面直角坐标系中画出这个函数的图象．

查看试题解析
21. 小聪和小明沿同一条路同时从学校出发到学校图书馆查阅资料，学校与图书馆的路程是 $4$ 千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达图书馆，图中折线 $O \to A \to B \to C$ 和线段 $O D$ 分别表示两人离学校的路程 $S$ （千米）与所经过的时间 $t$ （分钟）之间的函数关系，请根据图象回答下列问题：

(1)、小聪在图书馆查阅资料的时间为分钟，小聪返回学校的速度为千米/分钟；

(2)、请你求出小明离开学校的路程 $S$ （千米）与所经过的时间 $t$ （分钟）之间的函数关系；

(3)、求线段 $B C$ 的函数关系式；

(4)、当小聪与小明迎面相遇时，他们离学校的路程是多少千米？

查看试题解析
22. 已知二次函数y＝x²﹣4x+3．

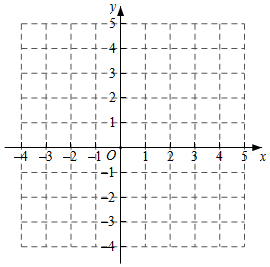(1)、在平面直角坐标系xOy中，描出二次函数图象的顶点A，与x轴的交点B、C，并画出此二次函数的图象（不必列表）；

(2)、根据图象，直接写出当x＜4时y的取值范围．

查看试题解析
23. 如图是二次函数y＝ax²+bx+c（a≠0）图象的一部分，对称轴为直线x＝1，根据图象完成下列问题：

(1)、请补充完整二次函数对称轴直线x＝1左边的函数图象．

(2)、请写出三个正确的结论．

查看试题解析
24. 《九章算术》中记载，浮箭漏（图①）出现于汉武帝时期，它由供水壶和箭壶组成，箭壶内装有箭尺，水匀速地从供水查流到箭壶，箭壶中的水位逐渐上升，箭尺匀速上浮，可通过读取箭尺读数计算时间，某学校STEAM小组仿制了一套浮箭漏，并从函数角度进行了如下实验探究：
（实验观察）实验小组通过观察，每2小时记录次箭尺读数，得到下表：

供水时间x（小时）

0

2

4

6

8

箭尺读数y（厘米）

6

18

30

42

54

（探索发现）

(1)、建立平面直角坐标系，如图②，横轴表示供水时间x ．纵轴表示箭尺读数y ，描出以表格中数据为坐标的各点．

(2)、观察上述各点的分布规律，判断它们是否在同一条直线上，如果在同一条直线上，求出这条直线所对应的函数表达式，如果不在同一条直线上，说明理由．
（结论应用）应用上述发现的规律估算：

(3)、供水时间达到12小时时，箭尺的读数为多少厘米？

(4)、如果本次实验记录的开始时间是上午8：00，那么当箭尺读数为90厘米时是几点钟？（箭尺最大读数为100厘米）

查看试题解析
25. 每年的3月12日是我国的植树节，某市园林局在3月12日当天安排甲、乙两个小组共种植220 棵株体较大的银杏树，要求在5小时内种植完毕．已知第1小时两个小组共植树35棵，甲组植树过程中由于起重机出故障，中途停工1个小时进行维修，然后提高工作效率，直到与乙组共同完成任务为止．设甲、乙两个小组植树的时间为x（小时），甲组植树数量为y_甲（棵），乙组植树数量为y_乙（棵），y_甲， y_乙与x之间的函数关系图象如图所示．

(1)、求y_乙与x之间的函数关系式，并写出x的取值范围；

(2)、求m ， n的值，并说明n的实际意义．

查看试题解析
26. 民族要复兴，乡村必振兴.2月21日发布的2021年中央一号文件，主题是全面推进乡村振兴，加快农业农村现代化．乡村振兴战略的实施效果要用农民生活富裕水平来评价，某合作社为尽快打开市场，对本地新产品进行线上和线下销售相结合的模式，具体费用标准如下：
线下销售模式：标价5元/千克，八折出售；

线上销售模式：标价5元/千克，九折出售，超过6千克时，超出部分每千克再让利1.5元．

根据以上信息回答下列问题：

(1)、请分别求出两种销售模式下所需费用y（元）与购买产品数量x（千克）之间的函数关系式；

(2)、当购买产品数量为多少时，两种销售模式所需费用相同；

(3)、若想购买这种产品10千克，请问选择哪种销售模式购买最省钱？

查看试题解析
27. 已知图形ABCDEF的相邻两边垂直，AB＝8cm．当动点M以2cm/s的速度沿图①的边框按B→C→D→E→F→A的路径运动时，△ABM的面积S随时间t的变化如图②所示．回答下列问题：

(1)、求a的值和EF的长度；

(2)、当点M运动到DE上时，求S与t的关系式．

查看试题解析
28. 如图1是一个大长方形减去一个小长方形后形成的图形，已知动点P以1cm/s的速度沿边框A→B→C→D→E→F的路径移动，相应的△AFP的面积S（cm²）与时间x（s）之间的关系如图2，若AF＝3cm，请求出：

(1)、图1中的BC的长是多少？

(2)、图2中的a是多少？

(3)、图1中的图形面积是多少？

(4)、图2中的b是多少？

查看试题解析
29. 如图，在平面直角坐标系中，函数y＝－x＋2的图象与x轴，y轴分别交于点A ， B ，与函数y＝ $\frac{1}{3}$ x＋b的图象交于点C（－2，m）．

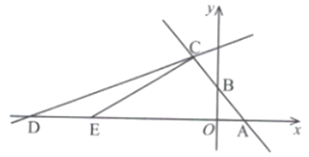(1)、求m和b的值；

(2)、函数y＝ $\frac{1}{3}$ x＋b的图象与x轴交于点D ，点E从点D出发沿DA向，以每秒2个单位长度匀速运动到点M（到A停止运动），设点E的运动时间为1秒．
①当ΔACE的面积为12时，求t的值；

②在点E运动过程中，是否存在t的值，使ΔACE为直角三角形？若存在，请求出t的值；若不存在，请说明理由．

查看试题解析