浙教版备考2022年中考数学一轮复习专题44 定义新运算
试卷更新日期:2022-01-13 类型:一轮复习
一、单选题
-
1. 若“!”是一种数学运算符号,并且1!=1, 2!=2 1=2, 3!=3 2 1=6,……,则 的值为( )A、 B、99! C、9900 D、 2!2. 现规定一种新运算“*”:a*b=(a﹣b)﹣|b﹣a|.则(﹣3)*2的值为( )A、10 B、0 C、-10 D、123. 对于有理数a、b定义一种新运算“⊙";规定: a⊙b =|a+b|+|a-b|则2⊙(-4)的值为( )A、8 B、6 C、4 D、24. 已知a , b是实数,定义:a※b=ab+a+b . 若m是常数x※(mx)=﹣1,下列说法正确的是( )A、方程一定有实数根 B、当m取某些值时,方程没有实数根 C、方程一定有两个实数根 D、方程一定有两个不相等的实数根5. 若存在一条线段把一个图形分钢成两个部分,使其中一个部分绕该线段中点旋转 后能与另一个部分重合,则我们把这个图形叫做旋转重合图形.下列图形中,属于旋转重合图形的是( )A、直角三角形 B、等边三角形 C、平行四边形 D、正五边形6. 现规定一种运算:a※b=ab+a-b,其中a,b为实数,则 ※ 等于( )A、-6 B、-2 C、2 D、67. 任意实数a,可用[a]表示不超过a的最大整数,如[4]=4,[ ]=1,现对72进行如下操作:72→[ ]=8→[ ]=2→[ ]=1,这样对72只需进行3次操作后变为1.类似地:对数字900进行了n次操作后变为1,那么n的值为( )A、3 B、4 C、5 D、68. 定义运算 ,若p≠1,q≠1,则下列等式中不正确的是( )A、
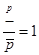 B、
B、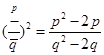 C、
C、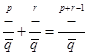 D、
D、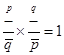 9. 刘谦的魔术表演风靡全国,小明也学起了刘谦发明了一个魔术盒,当有理数对(a,b)进入其中时,会得到一个新有理数:a2+b+1,例如把(3,-2)放入其中,就会得到32+(-2)+1=8.现将数对(-m,n)和数对(m,-n)分别放入其中,若得到的新有理数的值分别为x和y,则(x+y)是( )
9. 刘谦的魔术表演风靡全国,小明也学起了刘谦发明了一个魔术盒,当有理数对(a,b)进入其中时,会得到一个新有理数:a2+b+1,例如把(3,-2)放入其中,就会得到32+(-2)+1=8.现将数对(-m,n)和数对(m,-n)分别放入其中,若得到的新有理数的值分别为x和y,则(x+y)是( )
A、正数 B、非负数 C、0 D、负数10. 定义运算a⊕b=a(1﹣b),下面给出了这种运算的四个结论:①2⊕(﹣2)=6;②若a+b=0,则(a⊕a)+(b⊕b)=2ab;③a⊕b=b⊕a;④若a⊕b=0,则a=0或b=1.其中结论正确的有( )
A、①② B、①②③ C、②③④ D、①②④二、填空题
-
11. 符号“ ”表示和,如 ,则 .12. 对于任意实数对(a,b)和(c,d),规定运算“*”为(a,b)*(c,d)=(ac,bd);运算“⨁”为(a,b)⨁(c,d)=(a+c,b+d).若(1,2)*(p,q)=(2,﹣4),则(1,2)⨁(p,q)= .13. 我们把[a,b]称为-次函数y=ax+b的“特征数”.如果“特征数"是[2,n+1]的一次函数为正比例函数,则n的值为14. 定义:[a,b,c]为函数y=ax2+bx+c(a,b,c为实数)的“关联数”.若“关联数”为[m-2,m,1]的函数为一次函数,则m的值为15. 在实数的原有运算法则中,我们补充新运算法则“*”如下:当a≥b时,a*b=b2;当a<b时,a*b=a.那么,当x=2时,(1 * x)·x-(3* x)=(“·”和“-”仍为实数运算中的乘号和减号)16. 材料一:对于个位数字不为零的任意三位数M,将其个位数字与百位数字对调得到M',则称M'为M的“倒序数”,将一个数与它的“倒序数”的差的绝对值与99的商记为 .
例如523为325的“倒序数”, = =2;
材料二:对于任意三位数 满足,c>a,则称这个数为“登高数”.
(1)、 =;(2)、任意三位数M= ,求 的值是 .三、综合题
-
17. 符号“ ”称为二阶行列式,规定它的运算法规为: =ad-bc(1)、计算: =;(直接写出答案)(2)、化简二阶行列式:18. 定义新运算:a b=a(1-b) ,其中等号右边是常规的乘法和减法运算,例如:(-1) 1=(-1)×(1-1)=0.(1)、计算:(1+ ) ;(2)、小嘉说:“若a+b=0,则a a+b b= 2ab.”你是否同意他的观点?请说明理由.19. 在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的长方形的周长与面积的数值相等,则这个点叫做和谐点,如图,过点P分别作x轴、y轴的垂线,若与坐标轴围成的长方形OAPB的周长与面积的数值相等,则点P是和谐点.
 (1)、请判断点M(1,3),N(3,6)是不是和谐点,并说明理由;(2)、若和谐点P(a,3)在直线y=x+3b(b为常数)上,求a、b的值.20. 先阅读下面一段文字,再回答后面的问题:已知在平面直角坐标系内两点P1(x1 , y1) ,P2(x2 , y2),P1、P2两点间的距离P1P2= ,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2-x1|或|y2-y1| .(1)、已知A(1,3) ,B(-3,-5) ,试求A ,B两点间的距离;(2)、已知线段MN∥y轴,MN=4,若点M的坐标为(2,-1),试求点N的坐标;(3)、已知三角形DEF各顶点的坐标分别为D(0,6),E(-3,2),F(3,2) ,请判断该三角形的形状,并说明理由.21. 请你根据王老师所给的内容,完成下列各小题:
(1)、请判断点M(1,3),N(3,6)是不是和谐点,并说明理由;(2)、若和谐点P(a,3)在直线y=x+3b(b为常数)上,求a、b的值.20. 先阅读下面一段文字,再回答后面的问题:已知在平面直角坐标系内两点P1(x1 , y1) ,P2(x2 , y2),P1、P2两点间的距离P1P2= ,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2-x1|或|y2-y1| .(1)、已知A(1,3) ,B(-3,-5) ,试求A ,B两点间的距离;(2)、已知线段MN∥y轴,MN=4,若点M的坐标为(2,-1),试求点N的坐标;(3)、已知三角形DEF各顶点的坐标分别为D(0,6),E(-3,2),F(3,2) ,请判断该三角形的形状,并说明理由.21. 请你根据王老师所给的内容,完成下列各小题: (1)、如果x=-5,2⊙4=-18,求y的值;(2)、若1⊙1=8,4⊙2=20,求x,y的值.22. 对于任意四个有理数a , b , c , d , 可以组成两个有理数对(a , b)与(c , d).规定:(a , b)★(c , d)=ad-bc . 如:(1,2)★(3,4)=1×4-2×3=-2.
(1)、如果x=-5,2⊙4=-18,求y的值;(2)、若1⊙1=8,4⊙2=20,求x,y的值.22. 对于任意四个有理数a , b , c , d , 可以组成两个有理数对(a , b)与(c , d).规定:(a , b)★(c , d)=ad-bc . 如:(1,2)★(3,4)=1×4-2×3=-2.根据上述规定解决下列问题:
(1)、有理数对(5,-3)★(3,2)=;(2)、若有理数对(-3,x-1)★(2,2x+1)=15,则x=;(3)、若有理数对(2,x-1)★(k , 2x+k)的值与x的取值无关,求k的值.23. 对于有理数 , ,规定一种新运算: .(1)、计算:
(2)、若方程 ,求 的值.(3)、计算: 的值.24. 我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA ,容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题: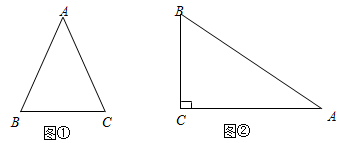 (1)、sad60°= , sad120°=(2)、如图②,在Rt△ABC中,∠ACB=90°,已知sinA ,试求sadA的值.(3)、直线y x+6与x轴,y轴分别交于点A,B,点M,N分别在线段AB,OA上,且△MON是等腰三角形,设△MON的顶角为θ,当sadθ 时,求点M的坐标.(请直接㝍出结果)25. 定义:在一个三角形中,若存在两条边x和y,使得 ,则称此三角形为“平方三角形”,x称为平方边.(1)、“若等边三角形为平方三角形,则面积为 ”是命题;“有一个角为30°且有一条直角边为2的直角三角形是平方三角形”是命题;(填“真”或“假”)(2)、如图,在△ABC中,D是BC上一点,若∠CAD=∠B,CD=1,求证:△ABC为平方三角形;
(1)、sad60°= , sad120°=(2)、如图②,在Rt△ABC中,∠ACB=90°,已知sinA ,试求sadA的值.(3)、直线y x+6与x轴,y轴分别交于点A,B,点M,N分别在线段AB,OA上,且△MON是等腰三角形,设△MON的顶角为θ,当sadθ 时,求点M的坐标.(请直接㝍出结果)25. 定义:在一个三角形中,若存在两条边x和y,使得 ,则称此三角形为“平方三角形”,x称为平方边.(1)、“若等边三角形为平方三角形,则面积为 ”是命题;“有一个角为30°且有一条直角边为2的直角三角形是平方三角形”是命题;(填“真”或“假”)(2)、如图,在△ABC中,D是BC上一点,若∠CAD=∠B,CD=1,求证:△ABC为平方三角形; (3)、若a,b,c是平方三角形的三条边,平方边a=2,若三角形中存在一个角为60°,求c的值.26. 在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x1 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“衍生矩形”.图为点P,Q的“衍生矩形”的示意图.
(3)、若a,b,c是平方三角形的三条边,平方边a=2,若三角形中存在一个角为60°,求c的值.26. 在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x1 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“衍生矩形”.图为点P,Q的“衍生矩形”的示意图. (1)、已知点A的坐标为(-1,0),点B的坐标为(2,4),求点A,B的“衍生矩形”的面积;(2)、已知点A的坐标为(-1,0),点C在直线x=2上,若点A,C的“衍生矩形"为正方形,求直线AC的解析式27. 阅读下面的文字,解答问题:
(1)、已知点A的坐标为(-1,0),点B的坐标为(2,4),求点A,B的“衍生矩形”的面积;(2)、已知点A的坐标为(-1,0),点C在直线x=2上,若点A,C的“衍生矩形"为正方形,求直线AC的解析式27. 阅读下面的文字,解答问题:大家知道 是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部写出来,于是小明用 -1来表示 的小数部分,你同意小明的表示方法吗? .
事实上,小明的表示方法是有道理的,因为 的整数部分是1,将 减去其整数部分,差就是 的小数部分.
例如: < < ,即2< <3, 的整数部分为2,小数部分为 -2.请解答:
(1)、 的整数部分是 , 小数部分是;(2)、如果 的小数部分为a, 的整数部分为b,求a+b- 的值;(3)、已知10+ =x+y,其中x是整数,且0<y<1,求x-y的相反数.28. 在实数范围内,方程x2=﹣1无解,为使开方运算在负数范围内可以进行,我们规定i2=﹣1.定义一种新数:Z=a+bi({a、b为实数}),并规定实数范围内的所有运算法则对于新数Z=a+bi({a、b为实数});仍然成立.例如:Z2=(a+bi)2=(a+bi)•(a+bi)=a2+2a•bi+(bi)2=a2﹣b2+2abi,若 ,则 ,依据上述规定,(1)、若 ,试求Z3的值;(2)、若 ,试求z2008的值.29. 在一个m(m≥3,m为整数)位的正整数中,若从左到右第n(n≤m,n为正整数)位上的数字与从右到左第n位上的数字之和都等于同一个常数k(k为正整数),则称这样的数为“对称等和数”.例如在正整数3186中,因为3+6=1+8=9,所以3186是“对称等和数”,其中k=9.再如在正整数53697中,因为5+7=3+9=6+6=12,所以53697是“对称等和数”,其中k=12.(1)、已知在一个能被11整除的四位“对称等和数”中k=4.设这个四位“对称等和数”的千位上的数字为s(1≤s≤9,s为整数),百位上的数字为t(0≤t≤9,t为整数), 是整数,求这个四位“对称等和数”;
(2)、已知数A,数B,数C都是三位“对称等和数”.A= (1≤a≤9,a为整数),设数B十位上的数字为x(0≤x≤9,x为整数),数C十位上的数字为y(0≤y≤9,y为整数),若A+B+C=1800,求证:y=﹣x+15.