2021-2022学年苏科版数学七年级下册7.2探索平行线的性质同步练习（培优）
试卷更新日期：2022-01-13 类型：同步测试
一、单选题
-
1. 如图，直线a // b，点B在直线b上，且AB⊥BC，∠2＝65°，则∠1的度数为 （ ）
A、65° B、45° C、35° D、25°2. 某人在练车场上练习驾驶汽车，两次拐弯后的行驶方向与原来的方向相反，则两次拐弯的角度可能是（ ）A、第一次向左拐40°，第二次向右拐40° B、第一次向左拐50°，第二次向右拐130° C、第一次向左拐70°，第二次向右拐110° D、第一次向左拐70°，第二次向左拐110°3. 如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=35°，则∠2的度数为（ ）
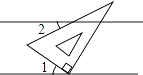A、10° B、20° C、25° D、30°4. 如图，AB∥CD，则根据图中标注的角，下列关系中成立的是（ ）
A、∠1=∠3 B、∠2+∠3=180° C、∠2+∠4＜180° D、∠3+∠5=180°5. 如图，AB∥CD，EMNF是直线AB、CD间的一条折线．若∠1=40°，∠2=60°，∠3=70°，则∠4的度数为（ ）
A、55° B、50° C、40° D、30°6. 如图，将长方形ABCD沿线段OG折叠到OB'C'G的位置，∠OGC'等于100°，则∠DGC'的度数为（ ）
A、20° B、30° C、40° D、50°7. 如图，给出下列推理：①∵∠B＝∠BEF，∴AB∥EF；②∵∠B＝∠CDE，∴AB∥CD；③∵∠B＋∠BEC＝180°，∴AB∥EF；④∵AB∥ CD，CD∥EF，∴AB∥EF.其中正确的推理是（ ）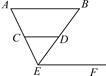
A、①②③ B、①②④ C、①③④ D、②③④8. 若将一副三角板按如图所示的方式放置，则下列结论不正确的是（ ）
A、∠1＝∠3 B、如果∠2＝30°，则有AC∥DE C、如果∠2＝30°，则有BC∥AD D、如果∠2＝30°，必有∠4＝∠C9.如图，给出下列条件：
①∠1=∠2；
②∠3=∠4；
③AD∥BE，且∠D=∠B；
④AD∥BE，且∠DCB=∠BAD；
其中能推出AB∥DC的条件为（ ）
A、①② B、②④ C、②③ D、②③④二、填空题
-
10. 如图，现将一块含有30°角的直角三角板的顶点放在平行线的一条直线上，与另一条直线的夹角为∠2，若∠1＝2∠2，那么∠1＝°.
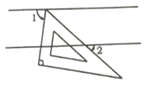11. 如图，直线l1∥l2 ， CD⊥AB于点D，∠1=40°，则∠2=度．
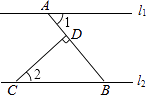12. 如图，把一张对面互相平行的纸条折成如图那样，EF是折痕，若∠EFB=34°，则下列结论正确有个1）∠C′EF=34°；（2）∠AEC=112°；（3）∠EFD=112°；（4）∠BGE=68°．
13.如图，AB∥CD，EG⊥AB于G，∠1=50°，则∠E =.
14. 如图，点D、E分别在AB、BC上，DE∥AC，AF∥BC，∠1=70°，则∠2=°．
15. 已知，如图，AB∥CD，则∠α、∠β、∠γ之间的关系为
16. 如果∠α与∠β的两边分别平行，∠α比∠β的3倍少36°，则∠α的度数是.三、综合题
-
17. 如图
(1)、已知：如图，直线AB、CD、EF被直线BF所截， ， .求证： ；(2)、你在（1）的证明过程中应用了哪两个互逆的真命题.18. 如图，在四边形ABCD中，连接BD，点E，F分别在AB和CD上，连接CE，AF，CE与AF分别交B于点N，M．已知∠AMD=∠BNC．
(1)、若∠ECD=60°，求∠AFC的度数；(2)、若∠ECD=∠BAF，试判断∠ABD与∠BDC之间的数量关系，并说明理由．19. 如图，AD⊥BC，垂足为D，点E、F分别在线段AB、BC上，∠CAD＝∠DEF，∠C+∠ADE＝90°.
(1)、求证：DE∥AC；(2)、判断EF与AD的位置关系，并证明你的猜想.20. 如图，已知AF分别与BD、CE交于点G、H，∠1=50°，∠2=130°.
(1)、BD与CE平行吗？为什么？(2)、若∠A=∠F，探索∠C与∠D的数量关系，并说明理由.21. 如图（a），已知∠BAG+∠AGD=180°，AE、EF、EG是三条折线段．
(1)、若∠E=∠F，如图（b）所示，求证：∠1=∠2；
(2)、根据图（a），写出∠1+∠E与∠2+∠F之间的关系，不需证明．22. 如图
(1)、问题情境：如图1，AB∥CD，∠PAB=135°，∠PCD=125°.求∠APC度数.小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可求得∠APC的度数.请写出具体求解过程.
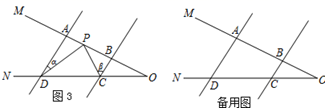
(2)、问题迁移：如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系？请说明理由；
(3)、在(1)的条件下，如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合)，请你直接写出∠CPD、∠α、∠β间的数量关系.