浙教版备考2022年中考数学一轮复习专题40 概率
试卷更新日期:2022-01-13 类型:一轮复习
一、单选题
-
1. 下列事件是必然事件的是( )A、任意选择某电视频道,它正在播新闻联播 B、温州今年元旦当天的最高气温为15℃ C、在装有白色和黑色的袋中摸球,摸出红球 D、不在同一直线上的三点确定一个圆2. 如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是( )
 A、 B、 C、 D、3. 投掷一枚普通的正方体骰子,有下列事件:①掷得的点数是6;②掷得的点数是奇数;③掷得的点数不大于4;④掷得的点数不小于2,这些事件发生的可能性由大到小排列正确的是( ).A、①②③④ B、④③②① C、③④②① D、②③①④4. 2012~2013年NBA整个常规赛季中,科比罚球投篮的命中率大约是83.3%,下列说法错误的是( ).A、科比罚球投篮2次,一定 全部命中 B、科比罚球投篮2次,不一定全部命中 C、科比罚球投篮1次,命中的可能性较大 D、科比罚球投篮1次,不命中的可能性较小5. 某小组做“用频率估计概率”的实验时,给出的某一结果出现的频率分布折线图,则符合这一结果的实验可能是( )
A、 B、 C、 D、3. 投掷一枚普通的正方体骰子,有下列事件:①掷得的点数是6;②掷得的点数是奇数;③掷得的点数不大于4;④掷得的点数不小于2,这些事件发生的可能性由大到小排列正确的是( ).A、①②③④ B、④③②① C、③④②① D、②③①④4. 2012~2013年NBA整个常规赛季中,科比罚球投篮的命中率大约是83.3%,下列说法错误的是( ).A、科比罚球投篮2次,一定 全部命中 B、科比罚球投篮2次,不一定全部命中 C、科比罚球投篮1次,命中的可能性较大 D、科比罚球投篮1次,不命中的可能性较小5. 某小组做“用频率估计概率”的实验时,给出的某一结果出现的频率分布折线图,则符合这一结果的实验可能是( ) A、抛一枚硬币,出现正面朝上 B、掷一个正六面体的骰子,出现3点朝上 C、从一个装有2个红球和1个黑球的袋子中任取一球,取到的是黑球 D、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃6. 在一个不透明的袋子中装有2个黄球和2个红球,它们除颜色外没有其他差别,从袋中任意摸出一个球,然后放回搅匀,再从袋中任意摸一个球,那么两次都摸到黄球的概率是( )A、 B、 C、 D、7. 下列说法正确的是( )A、掷一枚质地均匀的骰子,掷得的点数为3的概率是 B、某种彩票中奖的概率是 ,那么买10000张这种彩票一定会中奖 C、掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”的概率与“一枚硬币正面朝上,一枚硬币反面朝上”的概率相同 D、通过大量重复试验,可以用频率估计概率8. 某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的实验是( )
A、抛一枚硬币,出现正面朝上 B、掷一个正六面体的骰子,出现3点朝上 C、从一个装有2个红球和1个黑球的袋子中任取一球,取到的是黑球 D、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃6. 在一个不透明的袋子中装有2个黄球和2个红球,它们除颜色外没有其他差别,从袋中任意摸出一个球,然后放回搅匀,再从袋中任意摸一个球,那么两次都摸到黄球的概率是( )A、 B、 C、 D、7. 下列说法正确的是( )A、掷一枚质地均匀的骰子,掷得的点数为3的概率是 B、某种彩票中奖的概率是 ,那么买10000张这种彩票一定会中奖 C、掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”的概率与“一枚硬币正面朝上,一枚硬币反面朝上”的概率相同 D、通过大量重复试验,可以用频率估计概率8. 某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的实验是( )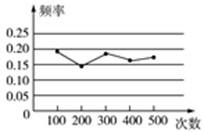 A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副去掉大、小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、掷一个质地均匀的正六面体骰子,向上的面点数是49. 某电视台一档综艺栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸,就不得奖,参与这个游戏的观众有三次翻牌机会(翻过的牌不能再翻).某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是( ).A、 B、 C、 D、10. 如图有6张写有数字的卡片,它们的背面都相同,现将它们背面朝上,从中任意一张是数字3的概率是( )
A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副去掉大、小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、掷一个质地均匀的正六面体骰子,向上的面点数是49. 某电视台一档综艺栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸,就不得奖,参与这个游戏的观众有三次翻牌机会(翻过的牌不能再翻).某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是( ).A、 B、 C、 D、10. 如图有6张写有数字的卡片,它们的背面都相同,现将它们背面朝上,从中任意一张是数字3的概率是( )
 A、
A、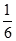 B、
B、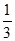 C、
C、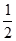 D、
D、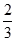 11. 在a2□4a□4的空格□中,任意填上“+”或“-”,在所得到的代数式中,能构成完全平方式的概率是( )A、1 B、0.5 C、0.75 D、0.25
11. 在a2□4a□4的空格□中,任意填上“+”或“-”,在所得到的代数式中,能构成完全平方式的概率是( )A、1 B、0.5 C、0.75 D、0.25二、填空题
-
12. 从分别写有2,4,5,6的四张卡片中任取一张,卡片上的数是偶数的概率为.13. 从甲、乙、丙三人中任选两人参加“青年志愿者”活动,甲被选中的概率为。14. 把一转盘先分成两个半圆,再把其中一个半圆等分成三等份,并标上数字如图所示,任意转动转盘,当转盘停止时,指针落在偶数区域的概率是.
 15. 小红的邮箱密码是一个六位数,每位上的数字都是0~9中的任一个,她忘了密码的最后一个数字,如果随意输人最后一位数字,则她正好能打开邮箱的概率是.16. 转动如图所示的一些可以自由转动的转盘,当转盘停止时,猜想指针落在黑色区域内的可能性大小,将转盘的序号按可能性从小到大的顺序排列为.
15. 小红的邮箱密码是一个六位数,每位上的数字都是0~9中的任一个,她忘了密码的最后一个数字,如果随意输人最后一位数字,则她正好能打开邮箱的概率是.16. 转动如图所示的一些可以自由转动的转盘,当转盘停止时,猜想指针落在黑色区域内的可能性大小,将转盘的序号按可能性从小到大的顺序排列为. 17. 任意选择电视的某一频道,正在播放新闻,这个事件是事件(填“必然”“不可能”或“随机”).
17. 任意选择电视的某一频道,正在播放新闻,这个事件是事件(填“必然”“不可能”或“随机”).三、综合题
-
18. 在一个不透明的口袋中装着大小、外形等一模一样的5个红球、3个蓝球和2个白球,它们已经在口袋中被搅匀了.请判断以下事件是可能发生,还是不可能发生,或者必然发生.(1)、从口袋中任意取出1个球,是一个白球;(2)、从口袋中一次任意取出5个球,全是蓝球;(3)、从口袋中一次任意取出5个球,只有蓝球和白球,没有红球;(4)、从口袋中一次任意取出6个球,恰好红、蓝、白三种颜色的球都齐全了;(5)、从口袋中一次任意取出6个球,有红色的球19. 如图,转盘黑色扇形和白色扇形的圆心角分别为120°和240°。

(注:当指针恰好指在分界线上时,无效重转)
(1)、让转盘自由转动一次,指针落在白色区域的概率是多少?(2)、让转盘自由转动两次,请用树状图或者列表法求出两次指针都落在白色区域的概率.20. 某同学报名参加校运动会,有以下5个项目可供选择:径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示)。
(1)、该同学从5个项目中任选一个,恰好是田赛项目的概率为;(2)、该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率。21. 2016年3月,我市某中学举行了“爱我中国•朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题: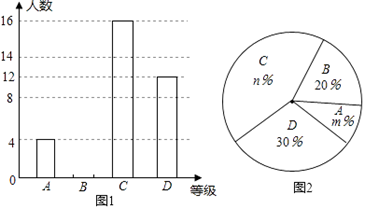 (1)、参加朗诵比赛的学生共有人,并把条形统计图补充完整;(2)、扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;(3)、学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.22. 深圳市某校艺术节期间,开展了“好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布表和频数分布直方图(如图),请你根据图中提供的信息,解答下列问题:
(1)、参加朗诵比赛的学生共有人,并把条形统计图补充完整;(2)、扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;(3)、学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.22. 深圳市某校艺术节期间,开展了“好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布表和频数分布直方图(如图),请你根据图中提供的信息,解答下列问题: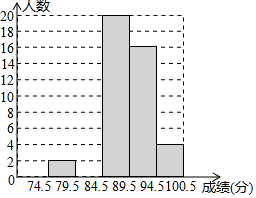
分组
频数
频率
74.5≤x<79.5
2
0.04
79.5≤x<84.5
a
0.16
84.5≤x<89.5
20
0.40
89.5≤x<94.5
16
0.32
94.5≤x<100.5
4
b
合计
50
1
(1)、频数、频率分布表中a= , b=;(2)、补全频数分布直方图;(3)、初赛成绩在94.5≤x<100.5分的四位同学恰好是七年级、八年级各一位,九年级两位,学生处打算从中随机挑选两位同学谈一下决赛前的训练,则所选两位同学恰好都是九年级学生的概率为 .23. 某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:九(1)班.88,91,92,93,93,93,94,98,98,100
九(2)班.89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级
最高分
平均分
中位数
众数
方差
九(1)班
100
m
93
93
12
九(2)班
99
95
n
93
8.4
(1)、直接写出表中m,n的值;(2)、依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;(3)、若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.24. 某中学号召学生利用假期开展社会实践活动,开学初学校随机地通过问卷形式进行了调查,将学生参加社会实践活动的天数,绘制成了下列两幅不完整的统计图:
请根据图中提供的信息,完成下列问题(填入结果和补全图形):
(1)、问卷调查的学生总数为人;(2)、扇形统计图中a的值为;(3)、补全条形统计图;(4)、该校共有1500人,请你估计“活动时间不少于5天”的大约有人;
(5)、如果从全校1 500名学生中任意抽取一位学生准备做交流发言,则被抽到的学生,恰好也参加了问卷调查的概率是 .25. 商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.(1)、若他去买一瓶饮料,则他买到奶汁的概率是;(2)、若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.26. 四张小卡片上分别写有数字1、2、3、4.它们除数字外没有任何区别,现将它们放在盒子里搅匀.(1)、随机地从盒子里抽取一张,求抽到数字2的概率;(2)、随机地从盒子里拙取一张.不放回再抽取第二张.请你用画树状图或列表的方法表示所有等可能的结果,并求抽到的数字之和为5的概率.27. 某中学为了预测本校应届毕业生“一分钟跳绳”项目的考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图1的部分频数分布直方图(从左到右依次为六个小组,每小组含最小值,不含最大值)和图2扇形统计图.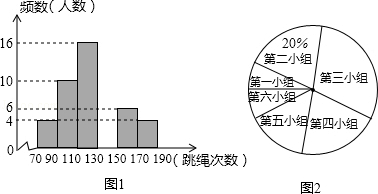
根据统计图提供的信息解答下列问题:
(1)、补全图1频数分布直方图,并指出这个样本数据的中位数落在第小组;(2)、若“一分钟跳绳”不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩的优秀人数;(3)、若“一分钟跳绳”成绩不低于170次的为满分,不低于130次的为优秀,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?28. 大家看过中央电视台“购物街”节目吗?其中有一个游戏环节是大转轮比赛,游戏工具是一个可绕轴心自由转动的圆形转轮,转轮按圆心角均匀划分为20等份,并在其边缘标记5、10、15、...、100共20个5的整数倍的数.选手依次转动转轮,每个人最多有两次机会,选手转动的数字之和最大且不超过100者为胜出;若超过100则成绩无效,称为“爆掉”.
(1)、某选手第一次转到了数字5,再转第二次,则他两次数字之和为100的可能性有多大?(2)、现在某选手第一次转到了数字65,若再转第二次了则有可能“爆掉”,请你分析“爆掉”的可能性有多大?29. 如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)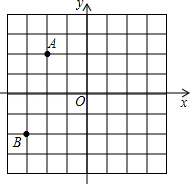 (1)、若点C与点A关于原点O对称,则点C的坐标为;(2)、将点A向右平移5个单位得到点D,则点D的坐标为;(3)、由点A,B,C,D组成的四边形ABCD内(不包括边界)任取一个横、纵坐标均为整数的点,求所取的点横、纵坐标之和恰好为零的概率.
(1)、若点C与点A关于原点O对称,则点C的坐标为;(2)、将点A向右平移5个单位得到点D,则点D的坐标为;(3)、由点A,B,C,D组成的四边形ABCD内(不包括边界)任取一个横、纵坐标均为整数的点,求所取的点横、纵坐标之和恰好为零的概率.