2021-2022学年苏科版数学七年级下册7.1探索直线平行的条件同步练习(培优)
试卷更新日期:2022-01-13 类型:同步测试
一、单选题
-
1. 如图,在四边形 中,连接 ,下列判断正确的是( )
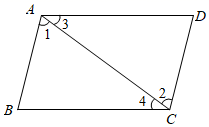 A、若 ,则 B、若 ,则 C、若 ,则 D、若 , ,则2. 如图,将一副三角板按如图放置,∠BAC=∠DAE=90°,∠B=45°,∠E=60°,则下列结论正确的有( )个.
A、若 ,则 B、若 ,则 C、若 ,则 D、若 , ,则2. 如图,将一副三角板按如图放置,∠BAC=∠DAE=90°,∠B=45°,∠E=60°,则下列结论正确的有( )个.
①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=30°,则有AC∥DE;④如果∠2=30°,则有BC∥AD.
A、4 B、3 C、2 D、13.如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的( )
 A、∠1=∠2 B、∠2=∠AFD C、∠1=∠AFD D、∠1=∠DFE4. 如图,已知∠1=∠2,其中能判定AB∥CD的是( )A、
A、∠1=∠2 B、∠2=∠AFD C、∠1=∠AFD D、∠1=∠DFE4. 如图,已知∠1=∠2,其中能判定AB∥CD的是( )A、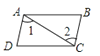 B、
B、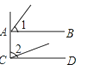 C、
C、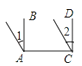 D、
D、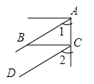 5. 下列说法正确的是( )A、如果两条直线被第三条直线所截,那么内错角必相等 B、如果两条直线被第三条直线所截,那么同位角的角平分线必平行 C、如果同旁内角互补,那么它们的角平分线必互相垂直 D、如果两角的两边分别平行,那么这两个角必相等6. 如图,下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+∠4=180°中,能判断直线l1∥l2的有( )
5. 下列说法正确的是( )A、如果两条直线被第三条直线所截,那么内错角必相等 B、如果两条直线被第三条直线所截,那么同位角的角平分线必平行 C、如果同旁内角互补,那么它们的角平分线必互相垂直 D、如果两角的两边分别平行,那么这两个角必相等6. 如图,下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+∠4=180°中,能判断直线l1∥l2的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
7.
如图,EF⊥AB于点F,CD⊥AB于点D,E是AC上一点,∠1=∠2,则图中互相平行的直线有 对.
 8. 长方形ABCD中,∠ADB=20°,现将这一长方形纸片沿AF折叠,若使AB′∥BD,则折痕AF与AB的夹角∠BAF应为
8. 长方形ABCD中,∠ADB=20°,现将这一长方形纸片沿AF折叠,若使AB′∥BD,则折痕AF与AB的夹角∠BAF应为 9.
9.如图所示,已知∠1=∠2,请你添上一个适当的条件 ,使AB∥CD.
 10. 一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数.
10. 一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数.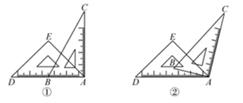 11. 如图,因为∠1=∠B,所以 . 理由是: . 因为∠2=∠B,所以 . 理由是: .
11. 如图,因为∠1=∠B,所以 . 理由是: . 因为∠2=∠B,所以 . 理由是: .
三、解答题
-
12.
如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么直线AB,CD的位置关系如何?
 13. 如图,四边形ABCD中,∠A=∠C=90°,BE、DF分别平分∠ABC、∠ADC,判断BE、DF是否平行,并说明理由.
13. 如图,四边形ABCD中,∠A=∠C=90°,BE、DF分别平分∠ABC、∠ADC,判断BE、DF是否平行,并说明理由.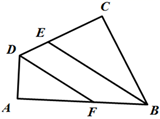 14.
14.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
 (1)、若∠DCE=45°,则∠ACB的度数为(2)、若∠ACB=140°,求∠DCE的度数(3)、由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.(4)、当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.15.
(1)、若∠DCE=45°,则∠ACB的度数为(2)、若∠ACB=140°,求∠DCE的度数(3)、由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.(4)、当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.15.如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数
(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.
(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过多少秒后边OC与边ON互相垂直.(直接写出答案)


