浙教版备考2022年中考数学一轮复习专题27 菱形
试卷更新日期：2022-01-13 类型：一轮复习
一、单选题
-
1. 如图，在△ABC中，点E 、D、F分别在边AB、BC、CA上，且DE∥AC，DF∥AB.下列说法中错误的是（ ）
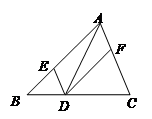A、四边形AEDF是平行四边形 B、如果∠BAC=90 °，那么四边形AEDF是矩形 C、如果AD⊥BC，那么四边形AEDF是正方形 D、如果AD平分∠BAC，那么四边形AEDF是菱形2. 如图，要拧开一个边长为a＝8mm的正六边形螺帽，扳手张开的开口b至少为（ ）
A、8 mm B、16mm C、8 mm D、4mm3. 如图，菱形ABCD的对角线AC与BD相交于点O，AC＝6，BD＝8，动点P从点B出发，沿着B→A→D在菱形ABCD的边AB，AD上运动，运动到点D停止.点P′是点P关于BD的对称点，连接PP'交BD于点M，若BM＝x（0＜x＜8），△DPP′的面积为y，下列图象能正确反映y与x的函数关系的是（ ）
A、
B、
C、
D、
4. 如图，已知AB＝8，P为线段AB上一个动点，分别以AP，PB为边在AB的同侧作菱形APCD和PBFE，点P，C，E在一条直线上，∠DAP＝60°，M，N分别是对角线AC，BE的中点，当点P在线段AB上移动时，点M，N之间的距离最短为（ ）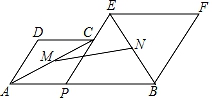
A、 B、 C、4 D、35. 如图，菱形ABCD的边长为a，点O是对角线AC上的一点，且OA＝a，OB＝OC＝OD＝1，则a等于（ ）
A、1 B、2 C、 D、6. 菱形有一个内角是120，且较短的对角线长为6cm，则菱形的边长为（ ）.A、6cm B、2 cm C、6 cm D、12 cm7. 如图，将边长为 的正方形ABCD沿对角线AC平移，使点A移至线段AC的中点A′处，得新正方形A′B′C′D′，新正方形与原正方形重叠部分（图中阴影部分）的面积是（ ）
A、 B、
C、1
D、
8. 如图，在▱ABCD中，对角线AC⊥AB，O为AC的中点，经过点O的直线交AD于E交BC于F，连结AF、CE，现在添加一个适当的条件，使四边形AFCE是菱形，下列条件：①OE＝OA；②EF⊥AC；③E为AD中点，正确的有（ ）个。
A、0 B、1 C、2 D、39. 如图，两张等宽的纸条交叉重叠在一起，重叠的部分为四边形ABCD，若测得A，C之间的距离为12cm，点B，D之间的距离为16m，则线段AB的长为（ ）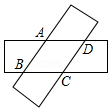
A、9.6cm B、10cm C、20cm D、12cm10. 如图，四边形ABCD是菱形，对角线AC＝8cm，BD＝6cm，DH⊥AB于点H，且DH与AC交于点G，AG＝ cm，则GH的长为（ ）
A、
cm
B、
cm
C、
cm
D、
cm
二、填空题
-
11. 如图，△ABC中，∠BAC=60°，∠B=45°，AB=2 ，点D是BC上的一个动点，D点关于AB，AC的对称点分别是E和F，四边形AEGF是平行四边形，则四边形AEGF的面积的最小值是.
12. 如图1，是一个 三节段式伸缩晾衣架，其支架侧面图（如图2）的基本图形是菱形。MN为衣架的墙体固定端，A为固定支点，B为滑动支点，四边形DFGI和四边形EIJH是菱形，且AF=BF=CH=DF=EH.点B在AN上滑动时，衣架外延钢体发生角度形变，其外延长度（点A和点C之间的距离）也随之变化，形成衣架伸缩效果。伸缩衣架为初始状态时，衣架外延长度（线段AC）为42cm。当点B向点A移动8cm时，外延长度（线段AC）为90cm.如图3，当外延长度(线段AC)为120cm时，则BD和GE的间距PQ长度为。
13. 如图，菱形中，对角线AC，BD交于点O，E为AD边中点，菱形ABCD的周长为28，则OE的长等于.
14. 如图，在菱形A BCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF=.
15. 已知一菱形的两对角线长为6cm和8cm，则其周长为cm，面积为cm。16. 如图，⊙O的半径为2，圆心O到直线l的距离为4，有一内角为60°的菱形，当菱形的一边在直线l上，另有两边所在的直线恰好与⊙O相切，此时菱形的边长为 ．
三、综合题
-
17. 如图，菱形 的对角线 与 交于点E， ， 的外接圆为 ．
(1)、求 的半径；(2)、分别判断点D和点E与 的位置关系，并说明理由．18. 如图，AB是⊙O的直径，C是半圆上任意一点，连接BC并延长到点D，使得CD＝CB，连接AD，点E是弧 的中点.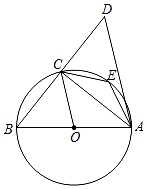
(1)、证明：△ABC≌△ADC.(2)、①当∠E＝°时，△ABD是直角三角形；②当∠D＝°时，四边形OAEC是菱形.
19. 如图，在△ABC中，D、E分别是AB、AC的中点，BE＝2DE，延长DE到点F，使得EF＝BE，连接CF.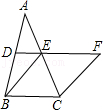
(1)、求证：四边形BCFE是菱形；(2)、若CE＝4，∠BCF＝120°，求菱形BCFE的面积.20. 如图，将△ABC沿着射线BC方向平移至△A′B′C′，使点A′落在∠ACB的外角平分线CD上，连结AA′．
(1)、判断四边形ACC′A′的形状，并说明理由；(2)、在△ABC中，∠B=90°，AB=8，cos∠BAC= ，求CB′的长．21. 已知，四边形ABCD是正方形，点P在直线BC上，点G在直线AD上(P，G不与正方形顶点重合，且在CD的同侧)，PD=PG， DF⊥PG于点H，交直线AB于点F，将线段PG绕点P逆时针旋转 ，连接EF．
(1)、如图1，当点P与点G分别在线段BC与线段AD上时．①求证：DG=2PC；
②求证：四边形PEFD是菱形；
(2)、如图2，当点P与点G分别在线段BC与线段AD的延长线上时，请猜想四边形PEFD是怎样的特殊四边形，并证明你的猜想．22. 菱形ABCD中，∠B=60°，点E在边BC上，点F在边CD上．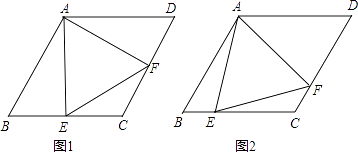
(1)、如图1，若E是BC的中点，∠AEF=60°，求证：BE=DF；(2)、如图2，若∠EAF=60°，求证：△AEF是等边三角形．23. 如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，
(1)、求证：∠DHO=∠DCO．(2)、若OC=4，BD=6，求菱形ABCD的周长和面积．24. 如图1，△ABD和△BDC都是边长为1的等边三角形．
(1)、四边形ABCD是菱形吗？为什么？(2)、如图2，将△BDC沿射线BD方向平移到△B1D1C1的位置，则四边形ABC1D1是平行四边形吗？为什么？(3)、在△BDC移动过程中，四边形ABC1D1有可能是矩形吗？如果是，请求出点B移动的距离（写出过程）；如果不是，请说明理由（图3供操作时使用）．25. 如图，在等边△ABC中，BC＝8cm，射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，同时点F从点B出发沿射线BC以2cm/s的速度运动，设运动时间为t（s）．
(1)、连接EF，当EF经过AC边的中点D时，求证：△ADE≌△CDF；(2)、填空：①当t为s时，以A、F、C、E为顶点的四边形是平行四边形；
②当t为s时，四边形ACFE是菱形．
26. 已知，如图，在平行四边形ABCD中，BF平分∠ABC交AD于点F，AE⊥BF于点O，交BC于点E，连接EF．
(1)、求证：四边形ABEF是菱形；(2)、若AE＝10，BF＝24，CE＝7，求四边形ABCD的面积．27. 如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD相交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE.
(1)、求证：四边形ABCD是菱形；(2)、若AB＝ ，BD＝2，求OE的长．
