浙教版备考2022年中考数学一轮复习专题25 多边形和平行四边形
试卷更新日期：2022-01-13 类型：一轮复习
一、单选题
-
1. 如图，在四边形ABCD 中，∠A+∠D=α，∠ABC 的平分线与∠BCD 的平分线交于点 P，则∠P=（ ）
A、90°﹣ α B、90°+ α C、 α D、360°﹣ α2. 如图是一枚“八一”建军节纪念章，其外轮廓是一个正五边形， 则图中∠1 的大小为（ ）．
A、120° B、36° C、108° D、90°3. 如图，在Rt△ABC中，AC＝BC＝3，∠ACB＝90°，将边长为1的正方形BDEF绕点B旋转一周，连结AE，点M为AE的中点，连结FM，则线段FM的最大值为（ ）
A、 B、 +1 C、2 D、 +14. 多边形的每个内角都等于150°，则从此多边形的一个顶点出发可作的对角线共有（ ）A、8条 B、9条 C、10条 D、11条5. 如图，AB，BC是⊙O的弦，∠B=60°，点O在∠B内，点D为 上的动点，点M，N，P分别是AD，DC，CB的中点.若⊙O的半径为2，则PN+MN的长度的最大值是（ ）
A、 B、 C、 D、6. 下列关于正多边形的叙述，正确的是（ ）A、正九边形既是轴对称图形又是中心对称图形 B、存在一个正多边形，它的外角和为720° C、任何正多边形都有一个外接圆 D、不存在每个外角都是对应每个内角两倍的正多边形7. 如图，在平行四边形 中， 是 延长线上一点， 与 、 分别交于点 、 ．则下列说法错误的是（ ）
A、 B、 C、 D、8. 如图，△ABC的中线BD，CE交于点O，连接OA，点G，F分别为OC，OB的中点，BC=8，A0=6，则四边形DEFG的周长为（ ）.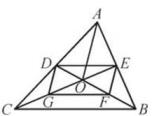
A、12 B、14 C、16 D、189. 如图，已知矩形ABCD中，R， P分别是DC，BC上的点，E，F分别是AP，RP的中点.当点P在BC上从点B向点C移动而点R不动时，那么下列结论成立的是（ ）.
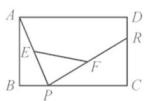A、线段EF的长逐渐增大 B、线段EF的长逐渐减少 C、线段EF的长不变 D、线段EF的长不能确定10. 如图，正方形ABCD的边长为6，点E在边CD上，且CD＝3DE.将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG，CF.则下列结论：①△ABG≌△AFG；②∠AGB+∠AED＝135°；③BG＝CG；④S△EGC＝S△AFE.其中正确的个数是（ ）
A、1 B、2 C、3 D、4二、填空题
-
11. 正五边形每个内角的度数为。12. 已知：如图，直线 AB、CD 相交于点 O，PE⊥AB 于点 E，PF⊥CD 于点 F，如果∠AOC=50°，那么∠EPF=度．
13. 如图，将 沿 、 翻折，顶点 均落在点O处，且 与 重合于线段 ，若 ，则 的度数 .
14. 若一个扇形的弧长为π，半径为2，则该扇形的面积为 ；若一个正多边形的外角为120度，则这个正多边形是正 边形.15. 如图，△ABC中，D，E分别是AB，AC的中点，F是DE上一点，且AF⊥FC，若BC=9，DF=1，则AC的长为.
16. 如图，四边形ABCD中，AD=BC，F，E，G分别是AB，CD，AC的中点，若∠DAC=20°，∠ACB=60°，则∠FEG=.
三、综合题
-
17. 如图，将六边形纸片 沿虚线剪去一个角 后，得到 ．
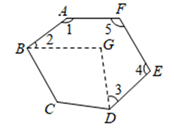(1)、求六边形 的内角和；(2)、求 的度数．18. 如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D，E分别在AC，BC上，且CD＝CE．
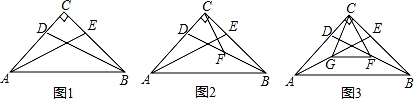(1)、如图1，求证：∠CAE＝∠CBD；(2)、如图2，F是BD的中点，求证：AE⊥CF；(3)、如图3，F，G分别是BD，AE的中点，若AC＝2 ，CE＝1，求△CGF的面积．19. 如图，在平行四边形ABCD中，对角线AC，BD交于点O，AC⊥BC，延长BC到点E，使得BC=CE，连结DE．
(1)、求证：四边形ACED是矩形；(2)、若AC=4，BD=6，求CD的长．20. 如图，在四边形ABCD中，AD// BC，AD=5cm， BC=8 cm，M是CD的中点，P是BC边上的一个动点(点P与点B， C不重合)，连接PM并延长交A D的延长线于点Q.
(1)、求证：△PCM≌OQDM；(2)、当BP取何值时，四边形A BPQ是平行四边形?并说明理由.21. 如图，在平行四边形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，AE=CG，AH=CF，且EG平分∠HEF.求证：
(1)、△AEH≌△CGF；(2)、四边形EFGH是菱形.22. 如图，将▱ABCD沿过点A的直线 折叠，使点D落到AB边上的点D ‘处，折痕 交CD边于点E，连接BE.
(1)、求证：四边形BCED’是平行四边形；(2)、若BE平分∠ABC，求证：AB2=AE2+BE2.23. 如图，请复制并剪出若干个纸样，通过拼图解答以下问题．
(1)、这种图形能密铺平面吗？如果你认为能，请用这种图形组成一幅镶嵌图案．(2)、若AB=4cm，AD=BC=1.5cm，由20个这种图形组成的镶嵌图形面积有多大？24. 正在改造的人行道工地上，有两种铺设路面材料：一种是长为acm、宽为bcm的矩形板材（如图1），另一种是边长为ccm的正方形地砖（如图2）．
(1)、用多少块如图2所示的正方形地砖能拼出一个新的正方形？（只要写出一个符合条件的答案即可），并写出新正方形的面积；(2)、现用如图1所示的四块矩形板材铺成一个大矩形（如图3）或大正方形（如图4），中间分别空出一个小矩形和一个小正方形．①试比较中间的小矩形和中间的小正方形的面积哪个大？大多少？
②如图4，已知大正方形的边长比中间小正方形的边长多20cm，面积大3200cm2 ． 如果选用如图2所示的正方形地砖（边长为20cm）铺设图4中间的小正方形部分，那么能否做到不用切割地砖就可直接密铺（缝隙忽略不计）呢？若能，请求出密铺所需地砖的块数；若不能，至少要切割几块如图2的地砖？
25. 如图，在四边形ABCD中，AB∥CD，BF=DE，AE⊥BD，CF⊥BD，垂足分别为E，F．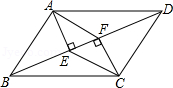
(1)、求证：△ABE≌△CDF；(2)、若AC与BD交于点O，求证：AC与BD互相平分．26. 如图，在△ABC中，∠ACB=90°，点D，E分别是BC，AB上的中点，连接DE并延长至点F，使EF=2DE，连接CE，AF．
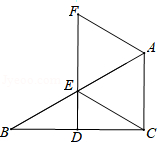(1)、证明：AF=CE；(2)、若∠B=30°，AC=2，连接BF，求BF的长．27. 乐乐和数学小组的同学们研究多边形对角线的相关问题，邀请你也加入其中！请仔细观察下面的图形和表格，并回答下列问题：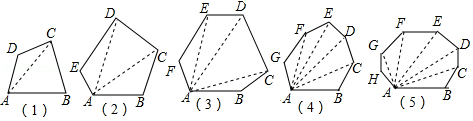
多边形的顶点数
4
5
6
7
8
……
n
从一个顶点出发的对角线的条数
1
2
3
4
5
……
①
多边形对角线的总条数
2
5
9
14
20
……
②
(1)、观察探究 请自己观察上面的图形和表格，并用含n的代数式将上面的表格填写完整，其中①；②；(2)、实际应用 数学社团共分为6个小组，每组有3名同学．同学们约定，大年初一时不同组的两位同学之间要打一个电话拜年，请问，按照此约定，数学社团的同学们一共将拨打电话多少个？(3)、类比归纳 乐乐认为（1）、（2）之间存在某种联系，你能找到这两个问题之间的联系吗？请用语言描述你的发现．28. Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．
(1)、若点 P 在线段 AB 上，如图（1）所示，且∠α=50°，则∠1+∠2=°；(2)、若点 P 在边 AB 上运动，如图（2）所示，则∠α、∠1、∠2 之间的关系为：；(3)、若点P运动到边 AB 的延长线上，如图（3）所示，则∠α、∠1、∠2 之间有何关系？猜想并说明理由．(4)、若点P运动到△ABC 形外，如图（4）所示，则∠α、∠1、∠2 之间的关系为： ．29. 操作与证明：
如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点c重合，点E，F分别在正方形的边CB，CD上，连接AF．取AF中点M，EF的中点N，连接MD，MN．
(1)、连接AE，求证：△AEF是等腰三角形；(2)、猜想与发现：在(1)的条件下，请判断DM，MN的数量关系和位置关系，得出结论．
结论1：DM，MN的数量关系是；
结论2：DM，MN的位置关系是；
(3)、拓展与探究：如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则(2)中的两个结论还成立吗?若成立，请加以证明；若不成立，请说明理由．