浙教版备考2022年中考数学一轮复习专题23 等腰三角形
试卷更新日期：2022-01-13 类型：一轮复习
一、单选题
-
1. 如图，将△ABC绕点B按逆时针方向旋转40°到△DBE（其中点D与点A对应，点E与点C对应），连接AD，若AD∥BC，则∠ABE的度数为（ ）
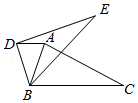A、25° B、30° C、35° D、40°2. 如图，△ABC与△CED均为等边三角形，且B，C，D三点共线.线段BE，AD相交于点O，AF⊥BE于点F.若OF＝1，则AF的长为（ ）
A、1 B、 C、 D、23. 如图，在等边△ABC中，D、E分别是BC、AC上的点，且AE＝CD，AD、BE相交于F点，BH⊥AD于H点，FH＝3，EF＝0.5，则AD的长为（ ）
A、6 B、6.5 C、7 D、7.54. 如图是一个6×6的正方形网格，每个小正方形的顶点都是格点，等腰△ABC的顶点都是图中的格点，其中点A、点B的位置如图所示，则点C可能的位置共有（ ）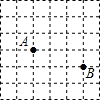
A、10个 B、9个 C、8个 D、7个5. 如图：BD⊥AC于点B，G是线段BD上一点(不与点B，点D重合)，且AB=BG，BD=BC，E，F分别为AD，CG的中点，AD=6，连结EF，DF，若△DEF为直角三角形，则DF的长度为（ ）
A、3 B、 C、3或 D、3或 或6. 已知等腰 中， 于点D，且 ，则 底角的度数为（ ）A、45°或75° B、60°或75° C、15°或75° D、45°或75°或15°7. 已知等腰三角形的周长为20，且一边长为12，则底边长为（ ）A、4 B、12 C、4或12 D、不存在8. 如图所示，在△ABC中，AB= AC，已知BD= 40，AB=50，AD=30，则△ABC的面积为（ ）
A、900 B、600 C、1200 D、24009. 如图，在△ABC中，AC=BC，∠C=36°，AD平分∠BAC，则图中等腰三角形的个数是（ ）
A、1 B、2 C、3 D、410. 如图， 和 均为等边三角形，且点E在 内， ，若 是不等边三角形，那么 的度数可能是（ ）
A、110° B、125° C、140° D、150°二、填空题
-
11. 如图，已知△ABC，AB=AC，∠A=70°。O，D分别为BC，AB的中点，以O为圆心，OD为半径作圆，与AB的另一个交点为E，与AC交于点G，F，则∠DOE+∠FOG的度数是.
12. 如图，在Rt△ABC中，∠A 90°，∠B 38°，点E，F分别在边BC，AC上，将△CEF沿EF所在的直线折叠，使C的对应点 落在AB上，且 E=B ，则∠AF = ．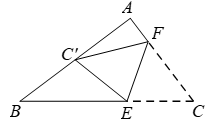
13. 如图所示，在△ABC中，AB=AC，AD是∠BAC的平分线，已知AB=5，AD=3，则BC的长为
14. 如图所示，在等腰△ABC中，AB= BC= 10，AC=16．则△ABC的面积为
15. 含30°角的直角三角板与直线l1 ， l2的位置关系如图所示，已知l1∥l2 ， ∠1=60°，以下三个结论中正确的是 (只填序号)．①AC=2BC；②△BCD为等边三角形；③AD=BD．
16. 如图，分别以线段BC的两个端点为圆心，大于 BC的长为半径画弧，两弧分别相交于D、E两点，直线DE交BC于点F，点A是直线DE上的一点，连接AB、AC，若AB=12 cm，∠C=60°，则CF= cm．
三、综合题
-
17. 定义：在一个三角形中，若存在两条边x和y，使得y＝x2 ， 则称此三角形为“平方三角形”，x称为平方边．
(1)、“若等边三角形为平方三角形，则面积为 ”是 命题；“有一个角为30°且有一条直角边为2的直角三角形是平方三角形”是 命题；（填“真”或“假”）
(2)、如图，在△ABC中，D是BC上一点，若∠CAD＝∠B，CD＝1，求证：△ABC为平方三角形；(3)、若a，b，c是平方三角形的三条边，平方边a＝2，若三角形中存在一个角为60°，求c的值．18. 如图，在△ABC中，∠ACB＝90°，AC＝BC，O是AB的中点，连接OC，点F、E分别在边AB和BC上，过E点作EM⊥AB，垂足为M，满足∠FCO＝∠EFM．
(1)、求证：CF＝EF；(2)、求证： ．19. 如图所示，直线y= x+ 与两坐标轴分别交于A，B两点．
(1)、求∠ABO的度数；(2)、过点A的直线l交x轴正半轴于点C，AB=AC，求直线l的函数解析式．20. 如图所示，把16个边长为1cm的正方形拼在一起，试解决下列问题：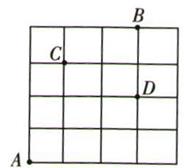
(1)、连接A到B，C，D的线段，哪几条的长度是无理数？(2)、△BCD是什么三角形，为什么？21. 如图所示，在△ABC中，∠ACB= 90°，以点B为圆心，BC长为半径画弧，交线段AB于点D；以点A为圆心，AD长为半径画弧，交线段AC于点E，连接CD．
(1)、若∠A=28°，求∠ACD的度数；(2)、设BC=3，AC=4，求AD的长．22. 数学课上，张老师举了下面的例题：例1：在等腰三角形ABC中，∠A=110°，求∠B的度数． (答案：35°)
例2：在等腰三角形ABC中，∠A=40°，求∠B的度数． (答案：40°或70°或100°)
张老师启发同学们进行变式，小敏编了如下一题：
变式：在等腰三角形ABC中，∠A=80°，求∠B的度数．
(1)、请你解答以上的变式题．(2)、解(1)后，小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同，如果在等腰三角形ABC中，设∠A=x°，当∠B有三个不同的度数时，请你探索x的取值范围．
23. 如图所示，△ABC是边长为6的等边三角形，P是AC边上一动点，由点A向点C运动(与A，C不重合)，Q是CB延长线上的一点，与点P同时以相同的速度由点B向CB延长线方向运动(Q不与B重合)，过点P作PE⊥AB于点E，连接PQ交AB于点D．
(1)、当∠BQD=30°时，求AP的长．(2)、试说明：在运动过程中，点D是线段PQ的中点．(3)、在运动过程中，线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化，请说明理由．24. 如图所示，已知线段AC∥y轴，点B在第一象限，且AO平分∠BAC，AB交y轴于点G，连接OB，OC．
(1)、判断△AOG的形状，并说明理由．(2)、若点B，C关于y轴对称，试说明：AO⊥BO．25. 先阅读下面一段文字，再回答后面的问题．已知在平面内两点P(x1 ， y1)、P(x2 ， y2)，这两点间的距离公式为P1P2= ，同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于
坐标轴时，两点间距离公式可简化为|x2-x1|或|y2-y1|
(1)、已知A(2，4)、B(-3，-8)，试求A、B两点间的距离；(2)、已知A、B在平行于y轴的直线上，点A的纵坐标．为5，点B的纵坐标为-1，试求A、B两点间的距离；(3)、已知一个三角形各顶点坐标为A(0，6)、B(-3，2)、C(3，2)，你能判断此三角形的形状吗？说明理由．26. 如图所示，已知等腰三角形ABC的底边BC=13cm，D是腰AB上一点，且CD=12cm，BD=5cm．
(1)、试说明：△BDC是直角三角形．(2)、求△ABC的周长．27. 如图1，在Rt△ABC中，∠C＝90°，AC＝BC＝4，点D、E分别在边AC、AB上，AD＝DE＝ AB，连接DE．将△ADE绕点A逆时针方向旋转，记旋转角为θ．
(1)、问题发现①当θ＝0°时， ＝；②当θ＝180°时， ＝ ．(2)、拓展探究：试判断：当0°≤θ＜360°时，BE的大小有无变化？请就图2的情形给出证明；(3)、问题解决：当△ADE旋转至B、D、E三点共线时，求线段CD的长．28. 如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连接AP并延长AP交CD于F点.
(1)、求证：四边形AECF为平行四边形；(2)、若△AEP是等边三角形，连接即，求证：△APB≌△EPC；(3)、若矩形ABCD的边AB=6，BC=4，求△CPF的面积.