浙教版备考2022年中考数学一轮复习专题19 图形初步
试卷更新日期:2022-01-13 类型:一轮复习
一、单选题
-
1. “三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任意一角.这个三等分角仪由两根有槽的棒OA、OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动,若∠ODE=99°,则∠CDE的度数是( )
 A、68° B、69° C、72° D、75°2. 已知 ,用尺规作图的方法在 BC上取一点P,使 ,下列选项正确的是( )A、
A、68° B、69° C、72° D、75°2. 已知 ,用尺规作图的方法在 BC上取一点P,使 ,下列选项正确的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列命题中,①在同一平面内,若 a⊥b , ,则 ;②相等的角是对顶角;③能被2整除的数也能被4整除;④两点之间线段最短.真命题有( )A、1个 B、2个 C、3个 D、4个4. 如图所示是一个三级台阶,它的每一级的长、宽、高分别2F为20 dm,3 dm,2 dm,A和B是这个台阶。上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )
3. 下列命题中,①在同一平面内,若 a⊥b , ,则 ;②相等的角是对顶角;③能被2整除的数也能被4整除;④两点之间线段最短.真命题有( )A、1个 B、2个 C、3个 D、4个4. 如图所示是一个三级台阶,它的每一级的长、宽、高分别2F为20 dm,3 dm,2 dm,A和B是这个台阶。上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )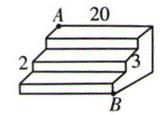 A、20dm B、25 dm C、30 dm D、35 dm5. 如图,已知∠1=∠2,则∠3的角平分线与∠4的角平分线( )
A、20dm B、25 dm C、30 dm D、35 dm5. 如图,已知∠1=∠2,则∠3的角平分线与∠4的角平分线( )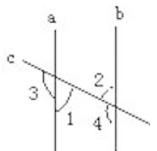 A、互相平行 B、相交 C、平行或相交 D、重合6. 将一个直角三角形绕它的最长边(斜边)旋转一周,得到的几何体是( ).A、
A、互相平行 B、相交 C、平行或相交 D、重合6. 将一个直角三角形绕它的最长边(斜边)旋转一周,得到的几何体是( ).A、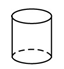 B、
B、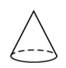 C、
C、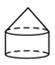 D、
D、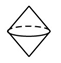 7. 如图 ,以 为边作 ,使 ,那么下列说法正确的是( )
7. 如图 ,以 为边作 ,使 ,那么下列说法正确的是( ) A、 B、∠AOC=∠AOB C、 D、 或8. 如图,在Rt△ABC中,∠ABC=90°,AB=BC,点P在△ABC内一点,连接PA,PB,PC,若∠BAP=∠CBP,且AP = 6,则PC的最小值是( )
A、 B、∠AOC=∠AOB C、 D、 或8. 如图,在Rt△ABC中,∠ABC=90°,AB=BC,点P在△ABC内一点,连接PA,PB,PC,若∠BAP=∠CBP,且AP = 6,则PC的最小值是( )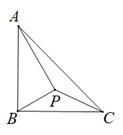 A、 B、 C、 D、9. 如图,在 中, ,AB=AC=5,点 在 上,且 ,点E是AB上的动点,连结 ,点 ,G分别是BC,DE的中点,连接 , ,当AG=FG时,线段 长为( )
A、 B、 C、 D、9. 如图,在 中, ,AB=AC=5,点 在 上,且 ,点E是AB上的动点,连结 ,点 ,G分别是BC,DE的中点,连接 , ,当AG=FG时,线段 长为( ) A、 B、 C、 D、410. 如图,一张矩形纸片沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于( )
A、 B、 C、 D、410. 如图,一张矩形纸片沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于( )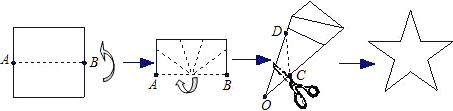 A、108° B、114° C、126° D、129°
A、108° B、114° C、126° D、129°二、填空题
-
11.
(1)、十边形的一个顶点的对角线把十边形分成个三角形.(2)、正多边形是指 , 的多边形.12. 如图,在直角三角形ABC中,∠ACB=90°,AB=7,点D是AB的中点,点P是斜边AB上的一个动点,FG是线段CP的垂直平分线,Q是FG上的一个动点,则PQ+QD的最小值为. 13. 如图,若∠α=38°,根据尺规作图的痕迹,则∠AOB的度数为 .
13. 如图,若∠α=38°,根据尺规作图的痕迹,则∠AOB的度数为 . 14. 从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
14. 从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 . 15. 在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为cm.(结果保留π)
15. 在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为cm.(结果保留π) 16. 一块方形蛋糕,一刀切成相等的两块,两刀最多切成4块,试问:五刀最多可切成块相等体积的蛋糕,十刀最多可切成块(要求:竖切,不移动蛋糕).
16. 一块方形蛋糕,一刀切成相等的两块,两刀最多切成4块,试问:五刀最多可切成块相等体积的蛋糕,十刀最多可切成块(要求:竖切,不移动蛋糕).三、综合题
-
17. 如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E,F.
 (1)、求证:DE=DF;(2)、若∠BDE =40°,求∠BAC的度数.18. 如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于点D,以点A为圆心,AD长为半径画弧,交线段AC于点E,连接CD.
(1)、求证:DE=DF;(2)、若∠BDE =40°,求∠BAC的度数.18. 如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于点D,以点A为圆心,AD长为半径画弧,交线段AC于点E,连接CD. (1)、若CA=28° ,求∠ACD的度数;(2)、若BC=3,AC=4,求AD的长.19. 在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC、BC于点M、N.
(1)、若CA=28° ,求∠ACD的度数;(2)、若BC=3,AC=4,求AD的长.19. 在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC、BC于点M、N. (1)、如图①,若∠BAC=110°,求∠EAN的度数;(2)、如图②,若∠BAC=80°,求∠EAN的度数;(3)、若∠BAC=α(α≠90°),直接写出∠EAN的大小(用含α的代数式表示).20. 用一块纸板做一个有底无盖的正方体粉笔盒,已知粉笔盒的容积为216cm3 .(1)、这个粉笔盒的棱长为多少?(2)、这块纸板的面积至少要多大?21. 如图所示是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:
(1)、如图①,若∠BAC=110°,求∠EAN的度数;(2)、如图②,若∠BAC=80°,求∠EAN的度数;(3)、若∠BAC=α(α≠90°),直接写出∠EAN的大小(用含α的代数式表示).20. 用一块纸板做一个有底无盖的正方体粉笔盒,已知粉笔盒的容积为216cm3 .(1)、这个粉笔盒的棱长为多少?(2)、这块纸板的面积至少要多大?21. 如图所示是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题: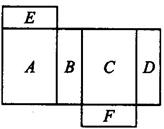 (1)、如果面A在多面体的上面,那么哪一面会在下面?(2)、如果面F在多面体的后面,从左面看是面B,那么哪一面会在上面?(3)、从右面看是面A,从上面看是面E,那么哪一面会在前面?22. 如图,圆锥底面的半径为10cm,高为10 cm.
(1)、如果面A在多面体的上面,那么哪一面会在下面?(2)、如果面F在多面体的后面,从左面看是面B,那么哪一面会在上面?(3)、从右面看是面A,从上面看是面E,那么哪一面会在前面?22. 如图,圆锥底面的半径为10cm,高为10 cm.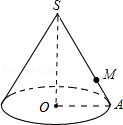 (1)、求圆锥的全面积;(2)、若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.23. 如图,直线 相交于点 于点 ,连接 .
(1)、求圆锥的全面积;(2)、若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.23. 如图,直线 相交于点 于点 ,连接 .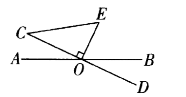 (1)、若 ,则 =;(2)、若 =2 cm, =1.5 cm, =2.5 cm,则点 到 的距离是cm.24. 已知∠A=72°15′48″,∠B=35°30′43″.(1)、求∠B的余角与∠A的补角的和;(2)、求∠A+2∠B的度数.25. 一副三角板ABC、DBE如图1放置,(∠D=30°、∠BAC=45°)
(1)、若 ,则 =;(2)、若 =2 cm, =1.5 cm, =2.5 cm,则点 到 的距离是cm.24. 已知∠A=72°15′48″,∠B=35°30′43″.(1)、求∠B的余角与∠A的补角的和;(2)、求∠A+2∠B的度数.25. 一副三角板ABC、DBE如图1放置,(∠D=30°、∠BAC=45°) (1)、求∠DBA的度数;(2)、若三角板DBE绕B点逆时针旋转,(如图2)在旋转过程中BM、BN分别平分∠DBA、∠EBC,则∠MBN如何变化;(3)、若三角板DBE绕B点逆时针旋转到如图3时,其它条件不变,则(2)的结论是否变化?
(1)、求∠DBA的度数;(2)、若三角板DBE绕B点逆时针旋转,(如图2)在旋转过程中BM、BN分别平分∠DBA、∠EBC,则∠MBN如何变化;(3)、若三角板DBE绕B点逆时针旋转到如图3时,其它条件不变,则(2)的结论是否变化?
26. (阅读理解):A,B,C为数轴上三点,若点C到A的距离CA是点C到B的距离CB的2倍,就称点C是(A,B)的好点.例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离CA是2,到点B的距离CB是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离DA是1,到点B的距离DB是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.(知识运用):
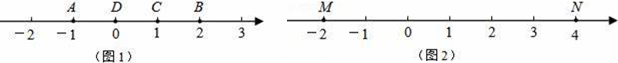
 (1)、如图1,表示数和的点是(A,B)的好点;(2)、如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.
(1)、如图1,表示数和的点是(A,B)的好点;(2)、如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.①表示数的点是(M,N)的好点;
②表示数的点是(N,M)的好点;
(3)、如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动.当t为何值时,P、A和B中恰有一个点为其余两点的好点?
27. 如图 (1)、【新知理解】
(1)、【新知理解】点 在线段 上, 若 或 , 则称点 是线段 的 “优点”, 线段 称 作互为"优点"伴侣线段。例如, 图1, 线段 的长度为6 , 点 在 上, 的长度为2 , 则点 是线段 的其中一个 “优点”。
①若点 为图1中线段 的 “优点” , 则 。
②若点 也是图1中线段 的 “优点” (不同于点 ), 则ACBD.(填 “ 或 “#”)
(2)、【解决问题 】如图 2, 数轴上有一点 表示的数为1, 向右平移3个单位到达点 ;
③若不同的两点 都在线段OF上, 且 均为线段OF的“优点”, 求线段 MN 的长;
④如图2, 若点 在射线 上, 且线段 与以 中某两个点为端点的线段互为 “优 点” 伴侣线段, 求点 表示的数 (写出所有可能)。
28. 已知:在四边形ABCD中,对角线AC,BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点G,∠BGE=∠ADE. (1)、如图①所示,试说明:AD=CD. .(2)、如图②所示,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图②中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.29. 已知线段AB=6.
(1)、如图①所示,试说明:AD=CD. .(2)、如图②所示,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图②中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.29. 已知线段AB=6. (1)、取线段AB的三等分点,这些点连同线段AB的两个端点可以组成多少条线段?求这些线段长度的和;(2)、再在线段AB上取两种点:第一种是线段AB的四等分点;第二种是线段AB的六等分点,这些点连同(1)中的三等分点和线段AB的两个端点可以组成多少条线段?求这些线段长度的和。
(1)、取线段AB的三等分点,这些点连同线段AB的两个端点可以组成多少条线段?求这些线段长度的和;(2)、再在线段AB上取两种点:第一种是线段AB的四等分点;第二种是线段AB的六等分点,这些点连同(1)中的三等分点和线段AB的两个端点可以组成多少条线段?求这些线段长度的和。