浙教版备考2022年中考数学一轮复习专题13 一次函数的图象与性质
试卷更新日期:2022-01-12 类型:一轮复习
一、单选题
-
1. 抛物线的顶点坐标是( )A、(3,1) B、(3,-1) C、(-3,1) D、(-3,-1)2. 一次函数y=x+2的图象与y轴的交点坐标为( )A、(2,0) B、(0,﹣2) C、(﹣2,0) D、(0,2)3. 把抛物线先向上平移2个单位,再向右平移3个单位,所得抛物线的解析式是( )A、 B、 C、 D、4. 数形结合是解决数学问题常用的思想方法.如图,直线y=2x-1与直线y=kx+b(k≠0)相交于点P(2,3).根据图象可知,关于x的不等式2x-1>kx+b的解集是( )
 A、x<2 B、x<3 C、x>3 D、x>25. 直线y=x+2与y轴的交点坐标是( )A、(0,2) B、(0,﹣2) C、(2,0) D、(﹣2,0)6. 小强和爷爷去爬山,爷爷先出发一段时间后小强再出发,途中小强追上了爷爷并最终先爬到山顶,两人所爬的高度h(米)与小强出发后的时间t(分钟)的函数关系如图所示,给出结论①山的高度是720米,②l1表示的是爷爷爬山的情况,l2表示的是小强爬山的情况;③小强爬山的速度是爷爷的2倍,④爷爷比小强先出发20分钟.其中正确的有( )
A、x<2 B、x<3 C、x>3 D、x>25. 直线y=x+2与y轴的交点坐标是( )A、(0,2) B、(0,﹣2) C、(2,0) D、(﹣2,0)6. 小强和爷爷去爬山,爷爷先出发一段时间后小强再出发,途中小强追上了爷爷并最终先爬到山顶,两人所爬的高度h(米)与小强出发后的时间t(分钟)的函数关系如图所示,给出结论①山的高度是720米,②l1表示的是爷爷爬山的情况,l2表示的是小强爬山的情况;③小强爬山的速度是爷爷的2倍,④爷爷比小强先出发20分钟.其中正确的有( ) A、1个 B、2个 C、3个 D、4个7. 若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )A、
A、1个 B、2个 C、3个 D、4个7. 若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )A、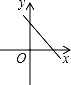 B、
B、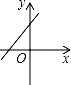 C、
C、 D、
D、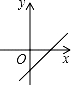 8. 大明因急事在运行中的自动扶梯上行走去二楼,图1中线段OA、OB分别大致表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )
8. 大明因急事在运行中的自动扶梯上行走去二楼,图1中线段OA、OB分别大致表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( ) A、
A、 B、
B、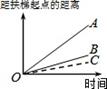 C、
C、 D、
D、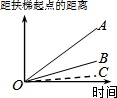 9. 若 则一次函数y=tx+t2的图象一定经过的象限是( )A、第一、二象限 B、第三、四象限 C、第一、二、三象限 D、第二、三、四象限10. 如图,直线y=ax+b与x轴交于点A(4,0),与直线y=mx交于点B(2,n),则关于x的不等式组0<ax-b<mx的解集为( )
9. 若 则一次函数y=tx+t2的图象一定经过的象限是( )A、第一、二象限 B、第三、四象限 C、第一、二、三象限 D、第二、三、四象限10. 如图,直线y=ax+b与x轴交于点A(4,0),与直线y=mx交于点B(2,n),则关于x的不等式组0<ax-b<mx的解集为( ) A、2<x<4 B、﹣4<x<﹣2 C、x>4 D、x<﹣211. 在平面直角坐标系中,点A(-3,3),B(-4,1),C(-2,1),点M(2,m)绕坐标原点O逆时针旋转90°后,恰好落在△ABC内部(不包括边界),则m的取值范围为( )
A、2<x<4 B、﹣4<x<﹣2 C、x>4 D、x<﹣211. 在平面直角坐标系中,点A(-3,3),B(-4,1),C(-2,1),点M(2,m)绕坐标原点O逆时针旋转90°后,恰好落在△ABC内部(不包括边界),则m的取值范围为( ) A、 <m< B、 <m< C、 <m< D、 <m<
A、 <m< B、 <m< C、 <m< D、 <m<二、填空题
-
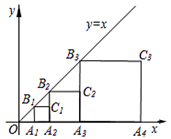
12. 某正比例函数的图象经过点( ,3),则此函数关系式为 .13. 若点A(1,y1),B(3,y2)在一次函数y=﹣x+b的图象上,则y1y2(填“>”“<”或“=”).14. 如图,已知直线 ,过点 作x轴的垂线交直线l于点 ,以 为边作正方形 ,过点 作x轴的垂线交直线l于点 ,以 为边作正方形 ,…;则点 的坐标为.
 15. 在平面直角坐标系中,点O为坐标原点,若直线y=﹣5x+5与x轴、y轴分别交于点A , B , 则△AOB的面积为 .16. 已知y与2z成反比例,比例系数为k1 , z与 x成正比例,比例系数为k2 , k1和k2是已知数,且k1•k2≠0,则y关于x成 比例.(填“正”或“反”)17. 等腰三角形中,底角的度数用x表示,顶角的度数用y表示,写出y关于x的函数解析式 , 函数的定义域 .
15. 在平面直角坐标系中,点O为坐标原点,若直线y=﹣5x+5与x轴、y轴分别交于点A , B , 则△AOB的面积为 .16. 已知y与2z成反比例,比例系数为k1 , z与 x成正比例,比例系数为k2 , k1和k2是已知数,且k1•k2≠0,则y关于x成 比例.(填“正”或“反”)17. 等腰三角形中,底角的度数用x表示,顶角的度数用y表示,写出y关于x的函数解析式 , 函数的定义域 .三、综合题
-
18. 已知y与3x﹣2成正比例,且当x=2时,y=8.(1)、求y与x的函数关系式;(2)、求当x=﹣2时的函数值;(3)、如果y与x的函数图象与x轴相交于点A , 图象与y轴相交于点B , 求 AOB的面积.19. 在弹性限度内,弹簧的长度与所挂物体质量满足一次函数关系,某数学兴趣小组通过实验发现弹簧的长度y(cm)与所挂物体质量x(kg)之间的关系如下表:
x/kg
0
1
2
3
⋯
y/cm
14.5
15
15.5
16
⋯
(1)、根据上表数据求出y与x之间的关系式;(2)、求当所挂物体的质量为6千克时弹簧的长度.20. 如图,直线y=kx+4与x轴相交于点A , 与y轴相交于点B , 且AB=2 . (1)、求点A的坐标;(2)、求k的值;(3)、C为OB的中点,过点C作直线AB的垂线,垂足为D , 交x轴正半轴于点P , 试求点P的坐标及直线CP的函数表达式.21. 甲、乙两商场出售相同的某种商品,每件售价均为3000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一件按原价收费,其余每件优惠20%;乙商场的优惠条件是:每件优惠25%.设所买商品为x(x>1)件,甲商场收费为 元,乙商场收费为y2元.(1)、分别求出y1 , y2与x之间的关系式;(2)、当所买商品为5件时,选择哪家商场更优惠?请说明理由.22. 2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价每件40元,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)、求点A的坐标;(2)、求k的值;(3)、C为OB的中点,过点C作直线AB的垂线,垂足为D , 交x轴正半轴于点P , 试求点P的坐标及直线CP的函数表达式.21. 甲、乙两商场出售相同的某种商品,每件售价均为3000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一件按原价收费,其余每件优惠20%;乙商场的优惠条件是:每件优惠25%.设所买商品为x(x>1)件,甲商场收费为 元,乙商场收费为y2元.(1)、分别求出y1 , y2与x之间的关系式;(2)、当所买商品为5件时,选择哪家商场更优惠?请说明理由.22. 2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价每件40元,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示. (1)、直接写出每月的销售量y(件)与销售单价x(元)之间的函数关系式 .(2)、设每月获得的利润为W(元),当销售单价为多少元时,销售这款文化衫每天所获得的利润最大,最大利润为多少元?(3)、该网店的营销部结合上述情况,提出了A,B两种营销方案:
(1)、直接写出每月的销售量y(件)与销售单价x(元)之间的函数关系式 .(2)、设每月获得的利润为W(元),当销售单价为多少元时,销售这款文化衫每天所获得的利润最大,最大利润为多少元?(3)、该网店的营销部结合上述情况,提出了A,B两种营销方案:方案A:销售单价高于进价且不超过进价20元.
方案B:每天销售量不少于220件,且每件文化衫的利润至少为35元.
请比较哪种方案的最大利润更高,并说明理由.
23. 已知一次函数y=1.5x-3. (1)、请在平面直角坐标系中画出此函数的图象.(2)、求出此函数与坐标轴围成的三角形的面积.24. 已知函数 的图象经过点 ,点
(1)、请在平面直角坐标系中画出此函数的图象.(2)、求出此函数与坐标轴围成的三角形的面积.24. 已知函数 的图象经过点 ,点 (1)、求直线 的解析式;(2)、若在直线 上存在点 ,使 ,求出点 坐标.25. 某经销商销售一种产品,这种产品的成本价为10元/件,规定销售价不低于成本价,且不高于35元,市场调查发现,该产品每天的销售量 (件)与销售价 (元/件)满足一次函数关系,如图所示.
(1)、求直线 的解析式;(2)、若在直线 上存在点 ,使 ,求出点 坐标.25. 某经销商销售一种产品,这种产品的成本价为10元/件,规定销售价不低于成本价,且不高于35元,市场调查发现,该产品每天的销售量 (件)与销售价 (元/件)满足一次函数关系,如图所示. (1)、求 与 之间的函数关系式;(2)、若经销商想要每天获得550元的利润,销售价应该定为多少?(3)、设每天的销售利润为 (元),当销售价为多少元时,每天获得的利润最大,最大利润是多少?26. 如图,直线y=kx﹣2与x轴,y轴分别交于B , C两点,其中OB=1.
(1)、求 与 之间的函数关系式;(2)、若经销商想要每天获得550元的利润,销售价应该定为多少?(3)、设每天的销售利润为 (元),当销售价为多少元时,每天获得的利润最大,最大利润是多少?26. 如图,直线y=kx﹣2与x轴,y轴分别交于B , C两点,其中OB=1. (1)、求k的值;(2)、若点A(x , y)是第一象限内的直线y=kx﹣2上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;(3)、在(2)的条件下,探索:
(1)、求k的值;(2)、若点A(x , y)是第一象限内的直线y=kx﹣2上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;(3)、在(2)的条件下,探索:①当点A运动到什么位置时,△AOB的面积是1;
②在①成立的情况下,x轴上是否存在一点P , 使△POA是等腰三角形?若存在,请写出满足条件的所有P点的坐标;若不存在,请说明理由.
27. 某剧院举行新年专场音乐会,成人票每张40元,学生票每张10元,剧院制定了两种优惠方案,且每个团体购票时只能选择其中一种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%付款.某校有4名老师与x(x≥4)名学生去观赏这次音乐会,设用方案1和方案2付款的总金额分别为y1(元)和y2(元).(1)、分别求出y1、y2与x之间的函数关系式;(2)、当学生人数为20名时,请通过计算说明哪种方案更优惠;(3)、请通过计算说明:当学生人数为多少时,选择两种方案一样优惠?28. 如图,直线l1:y1=ax﹣a , l1与x轴交于点B , 直线l2:y2= x+b , l2与x轴交于点A , 直线l1 , l2交于点C(2,﹣3). (1)、a=;点B的坐标为;(2)、求直线l2的解析表达式;(3)、求△ABC的面积.29. 我国边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防部迅速派出快艇B追赶(如图1).图2中l1、l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.根据图象回答问题:
(1)、a=;点B的坐标为;(2)、求直线l2的解析表达式;(3)、求△ABC的面积.29. 我国边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防部迅速派出快艇B追赶(如图1).图2中l1、l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.根据图象回答问题: (1)、直线l1与直线l2中表示B到海岸的距离与追赶时间之间的关系(2)、A与B比较,速度快;(3)、l1与l2对应的两个一次函数表达式S1=k1t+b1与S2=k2t+b2中,k1、k2的实际意义各是什么?并直接写出两个具体表达式(4)、15分钟内B能否追上A?为什么?(5)、当A逃离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?为什么?
(1)、直线l1与直线l2中表示B到海岸的距离与追赶时间之间的关系(2)、A与B比较,速度快;(3)、l1与l2对应的两个一次函数表达式S1=k1t+b1与S2=k2t+b2中,k1、k2的实际意义各是什么?并直接写出两个具体表达式(4)、15分钟内B能否追上A?为什么?(5)、当A逃离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?为什么?