2022届江苏省南京市中考数学零模卷

试卷更新日期：2022-01-12 类型：中考模拟

进入出卷网下载

一、单选题

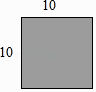
1. 据中央电视台新闻联播报道：今年4月我国国际收支口径的国际货物和服务贸易顺差337亿美元.用科学记数法表示337亿正确的是（）

A、337×10⁸ B、3.37×10¹⁰ C、3.37×10¹¹ D、0.337×10¹¹

查看试题解析
2. 下列运算正确的是（）

A、2a﹣a＝2 B、a³·a²＝a⁶ C、a³÷a＝a² D、（2a²）³＝6a⁵

查看试题解析
3. 如图是边长为10cm的正方形铁片，过两个顶点剪掉一个三角形，以下四种剪法中，裁剪线长度所标的数据（单位：cm）不正确的是（）

A、 B、 C、 D、

查看试题解析
4. 甲、乙两支同样的温度计按如图所示的位置放置，如果向左平移甲温度计，使其度数30正对着乙温度计的度数-20，那么此时甲温度计的度数-15正对着乙温度计的度数是（）

A、5 B、15 C、25 D、30

查看试题解析
5. 对于实数a，b，给出以下4个判断：①若|a|=|b|，则a=b；②若a＜b，则|a|＜|b|； ③若x²=81，则x=9；④若m=﹣5，则m²=25，其中正确的判断有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
6. 下列命题正确的是（）

A、三视图是中心投影 B、小华观察牡丹花，牡丹花就是视点 C、球的三视图均是半径相等的圆 D、阳光从矩形窗子里照射到地面上，得到的光区仍是矩形

查看试题解析

二、填空题

7. 若1<a<2，化简 $| a - 2 | + | 1 - a |$ 的结果是.

查看试题解析
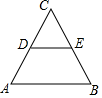
8. 在函数 $y = \frac{\sqrt{x + 1}}{2 x - 1}$ 中，自变量x的取值范围是.

查看试题解析
9. 计算： $\sqrt{\frac{1}{2}}$ ﹣ $\sqrt{8}$ + $\sqrt{32}$ = ．

查看试题解析
10. 设 $a ， b$ 是方程 $x^{2} + x - 2019 = 0$ 的两个实数根，则 $a^{2} + 2 a + b$ 的值为 .

查看试题解析
11. 如图，在△ABC中，D，E分别是AC，BC边上的中点，则三角形CDE的面积与四边形ABED的面积比等于

查看试题解析
12. 如图，在⊙O中，AE是直径，半径OD⊥弦AB，垂足为C，连接CE．若OC＝3，△ACE的面积为12，则CD＝．

查看试题解析
13. 如图，点A，B在反比例函数y＝ $\frac{k}{x}$ （k＞0）的图象上，线段AB分别交x轴、y轴于点C，D，AE⊥x轴于点E，BF⊥x轴于点F，若BF＝2AE，△ACE的面积是1，则k的值是.

查看试题解析
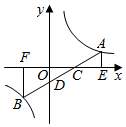14. 如图，⊙O经过A，B，C三点， $P A ， P C$ 分别与⊙O相切于点A，C，若 $∠ P = 40 °$ ，点B在优弧 $A C$ 上，则 $∠ B$ 的度数为 $°$ ．

查看试题解析
15. 在△ABC中，AB、AC的垂直平分线分别交BC于D、E，∠DAE＝20°，则∠BAC＝°.

查看试题解析
16. 如图，在平行四边形ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=4，则△CEF的周长为．

查看试题解析

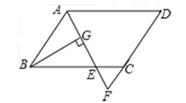
三、解答题

17. 解不等式 $2 (x - 1) < 4 - x$ ，并在数轴上表示出它的解集．

查看试题解析
18. 解分式方程： $\frac{3}{2 x - 4} - \frac{x}{x - 2} = \frac{1}{2}$ .

查看试题解析
19. 化简： $(1 - \frac{5}{x + 2}) \div \frac{x^{2} - 6 x + 9}{x + 2}$ .

查看试题解析
20. 如图，两车分别从路段AB两端同时出发，沿平行路线AC、BD行驶，CE和DF的长分别表示两车到道路AB的距离．

(1)、求证：△ACE∽△BDF；

(2)、如果两车行驶速度相同，求证：△ACE≌△BDF．

查看试题解析

21. 某工厂甲、乙两个部门各有员工400人，为了了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整.

收集数据从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如表：

甲	78	86	74	81	75	76	87	70	75	90
甲	75	79	81	70	74	80	86	69	83	77
乙	93	73	88	81	72	81	94	83	77	83
乙	80	81	70	81	73	78	82	80	70	40

整理、描述数据按如下分数段整理、描述这两组样本数据：

成绩x人数

部门

40≤x≤49

50≤x≤59

60≤x≤69

70≤x≤79

80≤x≤89

90≤x≤100

甲

乙

（说明：成绩80分及以上为生产技能优秀，70～79分为生产技能良好，60～69分为生产技能合格，60分以下为生产技能不合格）

分析数据两组样本数据的平均数、中位数、众数如表所示：

部门	平均数	中位数	众数	方差
甲	78.3	77.5	m	33.61
乙	78	n	81	117.5

得出结论

(1)、上表中m＝， n＝；

(2)、甲、乙两个部门员工的生产技能水平比较均衡的是部门，估计乙部门生产技能优秀的员工人数为；

(3)、可以推断出部门员工的生产技能水平较高，理由为.（至少从两个不同的角度说明推断的合理性）

查看试题解析

22. 4张相同的卡片分别写有数字1，2，3，4，将卡片的背面朝上，洗匀后从中任意抽取1张，将卡片上的数字作为被减数；一只不透明的袋子中装有标号为1，2，3的3个小球，这些球除标号外都相同，搅匀后从中任意摸出一个球，将摸到的球的标号作为减数．

(1)、求这两个数的差为0的概率；（用列表法或树状图说明）

(2)、如果游戏规则规定：当抽到的这两个数的差为非负数时，则甲获胜；否则，乙获胜．你认为这样的规则公平吗？如果不公平，请设计一个你认为公平的规则，并说明理由．

查看试题解析
23. 如图，1号楼在2号楼的南侧，楼间距为AB.冬至日正午，太阳光线与水平面所成的角为32.3°，1号楼在2号楼墙面上的影高为CA；春分日正午，太阳光线与水平面所成的角为55.7°，1号楼在2号楼墙面上的影高为DA.已知CD=35m.请求出两楼之间的距离AB的长度（结果保留整数）
（参考数据：sin32.3°≈0.53，cos32.3°≈0.85，tan32.3°≈0.63，sin55.7°≈0.83，cos55.7°≈0.56，tan55.7°≈1.47）

查看试题解析
24. 如图，平行四边形ABCD中，点E在BC上，且AE＝EC，试分别在下列两个图中按要求使用无刻度直尺画图.（保留作图痕迹）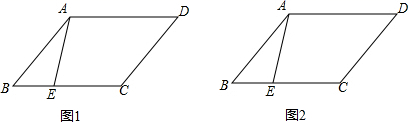

(1)、在图1中，画出∠DAE的平分线；

(2)、在图2中，画出∠AEC的平分线.

查看试题解析
25. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} - 4 a x + 3 a$ 与 $y$ 轴交于点A．

(1)、求点A的坐标（用含 $a$ 的式子表示）；

(2)、求抛物线与x轴的交点坐标；

(3)、已知点 $P (a, 0)$ ， $Q (0, a - 2)$ ，如果抛物线与线段 $P Q$ 恰有一个公共点，结合函数图象，求a的取值范围．

查看试题解析
26. 已知锐角 $△ A B C$ 的外接圆圆心为 $O$ ，半径为 $R$ .

(1)、求证： $\frac{A C}{\sin B} = 2 R$ ；

(2)、若 $△ A B C$ 中 $∠ A = 45 ° ， ∠ B = 60 ° ， A C = \sqrt{3}$ ，求 $B C$ 的长及 $\sin C$ 的值.

查看试题解析
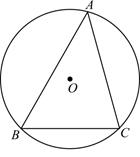27. 为了“创建文明城市，建设美丽家园”，我市某社区将辖区内的一块面积为1000m²的空地进行绿化，一部分种草，剩余部分栽花，设种草部分的面积为x（m²），种草所需费用y₁（元）与x（m²）的函数关系式为 $y_{1} = {\begin{matrix} k_{1} x (0 \leq x < 600) \\ k_{2} x + b (600 \leq x \leq 1000) \end{matrix}$ ，其图象如图所示：栽花所需费用y₂（元）与x（m²）的函数关系式为y₂=﹣0.01x²﹣20x+30000（0≤x≤1000）．

(1)、请直接写出k₁、k₂和b的值；

(2)、设这块1000m²空地的绿化总费用为W（元），请利用W与x的函数关系式，求出绿化总费用W的最大值；

(3)、若种草部分的面积不少于700m² ，栽花部分的面积不少于100m² ，请求出绿化总费用W的最小值．

查看试题解析

甲	78	86	74	81	75	76	87	70	75	90
甲	75	79	81	70	74	80	86	69	83	77
乙	93	73	88	81	72	81	94	83	77	83
乙	80	81	70	81	73	78	82	80	70	40

甲	78	86	74	81	75	76	87	70	75	90
甲	75	79	81	70	74	80	86	69	83	77
乙	93	73	88	81	72	81	94	83	77	83
乙	80	81	70	81	73	78	82	80	70	40

甲	78	86	74	81	75	76	87	70	75	90
甲	75	79	81	70	74	80	86	69	83	77
乙	93	73	88	81	72	81	94	83	77	83
乙	80	81	70	81	73	78	82	80	70	40