高中数学新人教A 必修一 函数性质 20道经典试题 期末复习练习卷
试卷更新日期:2022-01-12 类型:复习试卷
一、单选题
-
1. 下列函数不具备奇偶性的是( )A、 B、 C、 D、2. 下列函数中,既是奇函数,又是减函数的是( )A、 B、 C、 D、3. 若函数 为奇函数,则实数 ( ).A、-2 B、-1 C、0 D、14. 已知函数 , 为非零常数,则下列函数中为奇函数的是( )A、 B、 C、 D、5. 已知 是定义在 上的偶函数,则 ( )A、1 B、 C、-1 D、36. 已知是定义在R上的偶函数,且在上单调递增,则不等式的解集为( )A、 B、 C、 D、7. 函数在区间上单调递增,则的取值范围是有( )A、 B、 C、 D、8. 函数 的图像大致为( )A、
 B、
B、 C、
C、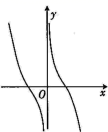 D、
D、 9. 奇函数 在区间 上是增函数,最大值为6,最小值为 ,则 的值为( )A、3 B、9 C、-3 D、-910. 已知函数 , 若 , 则的取值范围为( )A、 B、 C、 D、11. 已知是定义在上的减函数,那么的取值范围是( )A、 B、 C、 D、12. 函数 的图象可能是( )A、
9. 奇函数 在区间 上是增函数,最大值为6,最小值为 ,则 的值为( )A、3 B、9 C、-3 D、-910. 已知函数 , 若 , 则的取值范围为( )A、 B、 C、 D、11. 已知是定义在上的减函数,那么的取值范围是( )A、 B、 C、 D、12. 函数 的图象可能是( )A、 B、
B、 C、
C、 D、
D、 13. 已知偶函数 在 上单调递增,设 , , ,则a,b,c的大小关系为( )A、 B、 C、 D、14. 函数 在 上单调递增,且函数 是偶函数,则下列结论成立的是( )A、 B、 C、 D、15. 已知 是定义在 上的奇函数,且当 时, ,则当 时, ( )A、 B、 C、 D、16. 已如 的图像关于点 对称,且对 ,都有 成立,当 时, ,则 ( )A、-2 B、2 C、0 D、-817. 已知函数 满足对任意 ,都有 成立,则 的取值范围是( )A、(0,3) B、 C、(0,2] D、(0,2)
13. 已知偶函数 在 上单调递增,设 , , ,则a,b,c的大小关系为( )A、 B、 C、 D、14. 函数 在 上单调递增,且函数 是偶函数,则下列结论成立的是( )A、 B、 C、 D、15. 已知 是定义在 上的奇函数,且当 时, ,则当 时, ( )A、 B、 C、 D、16. 已如 的图像关于点 对称,且对 ,都有 成立,当 时, ,则 ( )A、-2 B、2 C、0 D、-817. 已知函数 满足对任意 ,都有 成立,则 的取值范围是( )A、(0,3) B、 C、(0,2] D、(0,2)