四川省内江市2022届高三理数第一次模拟考试试卷

试卷更新日期：2022-01-11 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知 $A = {x | - 2 < x < 1}$ ， $B = {y | y = x^{2}}$ ，则 $A \cup B =$ （）

A、 $(- 2 ， 0]$ B、 $(- 2 ， 0)$ C、 $(- 2 ， + \infty)$ D、 $[0 ， 1)$

查看试题解析
2. 已知 $i$ 为虚数单位，在复平面内，复数 $\frac{1 + i}{i} + i^{3}$ 对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. “事件A与事件B是对立事件”是“事件A与事件B是互斥事件”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 小李于2016年底贷款购置了一套房子，将通过10年期每月向银行还数额相同的房贷，且截止2020年底，他没有再购买第二套房子．下图是2017年和2020年小李的家庭收入用于各项支出的比例分配图，根据以上信息，判断下列结论中正确的是（）

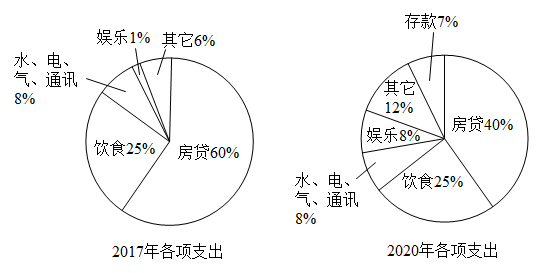A、小李一家2020年用于饮食的支出费用与2017年相同 B、小李一家2020年用于其他方面的支出费用是2017年的3倍 C、小李一家2020年的家庭收入比2017年增加了1倍 D、小李一家2020年用于房贷的支出费用比2017年减少了

查看试题解析
5. $(x - y) (x + y)^{5}$ 的展开式中， $x^{2} y^{4}$ 的系数为（）

A、-10 B、-5 C、5 D、10

查看试题解析
6. 记数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，若 $S_{n} = 2 a_{n} + 1$ ，则（）

A、 $a_{n} = 1$ B、 ${a_{n}}$ 是等差数列 C、 ${a_{n}}$ 是等比数列 D、 $S_{4} = - 30$

查看试题解析
7. 设 $a = 3^{\frac{1}{3}}$ ， $b = 6^{\frac{1}{6}}$ ， $c = l o g_{3} 2$ ，则（）

A、 $c < b < a$ B、 $b < c < a$ C、 $c < a < b$ D、 $a < c < b$

查看试题解析
8. 已知函数 $f (x) = 2 c o s (ω x + φ)$ （ $ω > 0$ ， $| φ | < \frac{π}{2}$ ）的部分图象如图所示，则 $f (x)$ 的解析式是（）

A、 $f (x) = 2 c o s (2 x - \frac{π}{3})$ B、 $f (x) = 2 c o s (2 x + \frac{π}{3})$ C、 $f (x) = 2 c o s (\frac{14}{11} x - \frac{π}{3})$ D、 $f (x) = 2 c o s (\frac{14}{11} x + \frac{π}{3})$

查看试题解析
9. 已知函数 $f (x)$ 是 $R$ 上单调递减的奇函数，数列 ${a_{n}}$ 为等差数列．若 $a_{2} > 0$ ，则 $f (a_{1}) +$ $f (a_{2}) + f (a_{3})$ 的值（）

A、恒为0 B、恒为正数 C、恒为负数 D、可正可负

查看试题解析
10. 已知α为锐角，且 $c o s α \cdot (1 + \sqrt{3} t a n 10 °) = 1$ ，则α的值为（）

A、70° B、60° C、50° D、40°

查看试题解析
11. 一种药在病人血液中的量保持在1500mg以上才有效，而低于500mg病人就有危险．现给某病人注射了这种药2500mg，如果药在血液中以每小时10%的比例衰减，为了充分发挥药物的利用价值，应该经过（）小时向病人的血液补充这种药．（附：lg2≈0.3010，lg3≈0.4771，答案采取四舍五入精确到0.1）

A、8.8小时 B、4.8小时 C、3.5小时 D、2.3小时

查看试题解析
12. 设 $a > 0$ ， $b > 0$ ，则 $\frac{8 a + 8 b}{3 a + 4 \sqrt{a b}}$ 的最小值是（）

A、4 B、 $2 \sqrt{2}$ C、2 D、1

查看试题解析

二、填空题

13. 已知向量 $\vec{a} = (2 ， λ)$ ， $\vec{b} = (3 ， - 6)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $λ =$ ．

查看试题解析
14. 已知 $f (x)$ 是定义在 $R$ 上的奇函数，且 $f (1 - x) = f (5 - x)$ ，当 $x \in (0 ， 2]$ 时， $f (x) = x + m$ ，则m= ．

查看试题解析
15. 如图，某小区有一块扇形OPQ空地，现打算在 $\overset{⌢}{P Q}$ 上选取一点C，按如图方式规划一块矩形ABCD土地用于建造文化景观．已知扇形OPQ的半径为6米，圆心角为60°，则矩形ABCD土地的面积（单位：平方米）的最大值是．

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} e^{x + 1} ， x \leq - 1 ， \\ l n (x + 1) ， x > - 1 ， \end{array}$ ， $g (x) = f (x) - m x - m + 1$ ，若 $g (x)$ 存在2个零点，则实数m的取值范围是．

查看试题解析

三、解答题

17. 在 $△ A B C$ 中，内角A、B、C的对边分别为a、b、c，满足 $2 a c o s A = b c o s C + c c o s B$ ．

(1)、求A的大小；

(2)、若 $a = 2 \sqrt{7}$ ， $△ A B C$ 的面积为 $6 \sqrt{3}$ ，求 $△ A B C$ 的周长．

查看试题解析
18. 某兴趣小组为了研究昼夜温差大小与患感冒人数多少之间的关系，请一所中学校医务室人员统计近期昼夜温差情况和到该校医务室就诊的患感冒学生人数，如下是2021年10月、11月中的5组数据：
日期
10月8日
10月18日
10月28日
11月8日
11月18日
昼夜温差x（℃）
8
11
6
15
5
就诊人数y
13
17
12
19
9

(1)、通过分析，发现可用线性回归模型拟合就诊人数y与昼夜温差x之间的关系，请用以上5组数据求就诊人数关于昼夜温差的线性回归方程 $y = b x + a$ （结果精确到0.01）；

(2)、一位住校学生小明所患感冒为季节性流感，传染给同寝室每个同学的概率为0.6．若该寝室的另3位同学均未患感冒，在与小明近距离接触后有X位同学被传染季节性流感，求 $X$ 的分布列和期望．
参考数据： $\sum_{i = 1}^{5} (x_{i} - x) (y_{i} - y) = 63$ ， $\sum_{i = 1}^{5} {(_{x} - x)}^{2} = 66$ ．
参考公式： $b = \frac{\sum_{i = 1}^{n} (x_{i} - x) (y_{i} - y)}{\sum_{i = 1}^{n} {(_{x} - x)}^{2}}$ ， $a = y - b x$ ．

查看试题解析
19. 在① $S_{2} = 2 S_{1} + S_{24} - 2$ ， ② $\frac{S_{9}}{9} = \frac{S_{15}}{15} + 6$ ， ③ $\frac{a_{10}^{2} - a_{6}^{2}}{a_{7}^{2} - a_{3}^{2}} = \frac{3}{5}$ 这三个条件中任选一个，补充在下面问题中．
问题：已知 ${a_{n}}$ 是等差数列，其前n项和为 $S_{n}$ ， $a_{12} = 1$ ， ▲ ，是否存在正整数m，n， $1 \leq m < n$ ，使得 $S_{m} = S_{n}$ 成立？若存在，求出正整数m，n满足的关系式；若不存在，请说明理由．
注：若选择多个条件分别解答，则按第一个解答计分．

查看试题解析
20. 已知a， $b \in R$ ，函数 $f (x) = a x^{3} + b x^{2} - x + 2$ ．

(1)、若函数 $f (x)$ 在点 $(1 ， 1)$ 处的切线与x轴平行，求a，b的值；

(2)、 $b = 3 a$ ，过点 $(0 ， 0)$ 可以作曲线 $y = f (x)$ 的三条切线，求实数a的取值范围．

查看试题解析
21. 已知函数 $f (x) = l n (a x + 1) - \frac{x - 1}{x + 1} (x > 0)$ ．

(1)、设 $a > 0$ ，讨论 $f (x)$ 的单调性；

(2)、若 $f (x) + (x - 2) e^{x} > l n 2 - e$ 恒成立，求实数a的取值范围．

查看试题解析
22. 在平面直角坐标系xOy中，已知曲线C的参数方程为 ${\begin{array}{l} x = 2 c o s α \\ y = 3 s i n α \end{array}$ （α为参数），直线l的参数方程为 ${\begin{array}{l} x = t c o s β \\ y = t s i n β \end{array}$ （t为参数），以原点O为极点，以x轴正半轴为极轴建立极坐标系．

(1)、写出曲线C和直线l的极坐标方程；

(2)、设直线l与曲线C交于A、B两点，点P的直角坐标为 $(\frac{1}{2} ， \frac{\sqrt{3}}{2})$ ，若点P在直线l上，求 $| P A | \cdot | P B |$ 的值．

查看试题解析
23. 已知函数 $f (x) = | x - 2 | + | 2 x - 1 |$ ．

(1)、求不等式 $f (x) ≥ 3$ 的解集；

(2)、记函数f（x）的最小值为m，若a，b，c均为正实数，且 $\frac{1}{2} a + b + c = m$ ，求a²+b²+c²的最小值．

查看试题解析

日期	10月8日	10月18日	10月28日	11月8日	11月18日
昼夜温差x（℃）	8	11	6	15	5
就诊人数y	13	17	12	19	9