上海市奉贤区2022届高三数学一模试卷

试卷更新日期：2022-01-11 类型：高考模拟

进入出卷网下载

一、填空题

1. 已知集合 $A = {1 ， 2} ， B = {2 ， a}$ ，若 $A ∪ B = {1 ， 2 ， 3}$ ，则 $a =$ .

查看试题解析
2. 计算 $\underset{n \to \infty}{l i m} \frac{7 n + 4}{5 - 3 n} =$ .

查看试题解析
3. 已知圆的参数方程为 ${\begin{array}{l} x = 2 c o s θ \\ y = 2 s i n θ \end{array}$ （ $θ$ 为参数），则此圆的半径是.

查看试题解析
4. 函数 $y = \sqrt{3} s i n x - c o s x$ 的最小正周期是.

查看试题解析
5. 函数 $y = x^{3} + a c o s x$ 是奇函数，则实数 $a =$ .

查看试题解析
6. 若圆锥的底面面积为 $π$ ，母线长为2，则该圆锥的体积为.

查看试题解析
7. 函数 $y = l g \frac{3 - 2^{x}}{3 + 2^{x}}$ 的定义域是.

查看试题解析
8. 等差数列 ${a_{n}}$ 满足 $a_{3} + a_{2} = 8 ， a_{4} + a_{3} = 12$ ，则数列 ${a_{n}}$ 前 $n$ 项的和为.

查看试题解析
9. 汽车前灯反射镜与轴截面的交线是抛物线的一部分，灯口所在的圆面与反射镜的轴垂直，灯泡位于抛物线焦点处，已知灯口的直径是24 cm，灯深10 cm，那么灯泡与反射镜顶点(即截得抛物线顶点)间的距离是.

查看试题解析
10. 已知曲线 $\frac{x^{2}}{a} + \frac{y^{2}}{16} = 1$ 的焦距是10，曲线上的点 $P$ 到一个焦点的距离是2，则点 $P$ 到另一个焦点的距离为.

查看试题解析
11. 从集合 ${0 ， 1 ， 2 ， 3 ， 4 ， 5 ， 6 ， 7 ， 8 ， 9}$ 中任取3个不同元素分别作为直线方程 $A x + B y + C = 0$ 中的 $A ， B ， C$ ，则经过坐标原点的不同直线有条（用数值表示）

查看试题解析
12. 设平面上的向量 $a ， b ， x ， y$ 满足关系 $a = y - x ， b = m x - y (m \geq 2)$ ，又设 $a$ 与 $b$ 的模均为1且互相垂直，则 $x$ 与 $y$ 的夹角取值范围为.

查看试题解析

二、单选题

13. 下列函数中为奇函数且在 $R$ 上为增函数的是（）

A、 $y = 2^{x}$ B、 $y = | x |$ C、 $y = s i n x$ D、 $y = x^{3}$

查看试题解析
14. 已知 ${(\sqrt{x} + \frac{1}{2 \sqrt[4]{x}})}^{n}$ 的二项展开式中，前三项系数成等差数列，则 $n$ 的值为（）

A、7 B、8 C、9 D、10

查看试题解析
15. 对于下列命题：
①若 $a > b > 0 ， c > d > 0 ，$ 则 $\frac{a + c}{d} > \frac{b + d}{c}$ ；
②若 $a > b > 0 ， c > d > 0$ ，则 $a^{c} > b^{d}$ .
关于上述命题描述正确的是（）

A、①和②均为真命题 B、①和②均为假命题 C、①为真命题，②为假命题 D、①为假命题，②为真命题

查看试题解析
16. 复数 $(c o s 2 θ + i s i n 3 θ) \cdot (c o s θ + i s i n θ)$ 的模为1，其中 $i$ 为虚数单位， $θ \in [0 ， 2 π]$ ，则这样的 $θ$ 一共有（）个.

A、9 B、10 C、11 D、无数

查看试题解析

三、解答题

17. 在 $△ A B C$ 中， $A ､ B ､ C$ 所对边 $a ､ b ､ c$ 满足 $(a + b - c) (a - b + c) = b c$ .

(1)、求 $A$ 的值；

(2)、若 $a = \sqrt{3}$ ， $c o s B = \frac{4}{5}$ ，求 $△ A B C$ 的周长.

查看试题解析
18. 第一象限内的点 $P$ 在双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 上，双曲线的左､右焦点分别记为 $F_{1} ､ F_{2}$ ，已知 $P F_{1} ⊥ P F_{2} ， | P F_{1} | = 2 | P F_{2} | ， O$ 为坐标原点.

(1)、求证： $b = 2 a$ ；

(2)、若 $△ O F_{2} P$ 的面积为2，求点 $P$ 的坐标.

查看试题解析
19. 图1是某会展中心航拍平面图，由展览场馆､通道等组成，可以假设抽象成图2，图2中的大正方形 $A A_{1} A_{2} A_{3}$ 是由四个相等的小正方形（如 $A B C D$ ）和宽度相等的矩形通道组成.展览馆可以根据实际需要进行重新布局成展览区域和休闲区域，展览区域由四部分组成，每部分是八边形，且它们互相全等.图2中的八边形EFTSHQMG是小正方形 $A B C D$ 中的展览区域，小正方形 $A B C D$ 中的四个全等的直角三角形是休闲区域，四个八边形是整个的展览区域，16个全等的直角三角形是整个的休闲区域.设 $A B C D$ 的边长为300米， $△ A E F$ 的周长为180米.

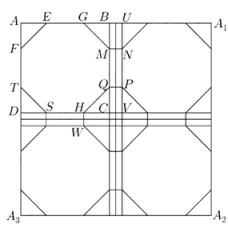(1)、设 $A E = x$ ，求 $△ A E F$ 的面积 $y$ 关于 $x$ 的函数关系式；

(2)、问 $A E$ 取多少时，使得整个的休闲区域面积最大.( $\sqrt{2} \approx 1.414$ ，长度精确到1米，利用精确后的长度计算面积，面积精确到1平方米)

查看试题解析
20. 如图，在正四棱锥 $P - A B C D$ 中， $P A = A B = 2 \sqrt{2}$ ， $E ､ F$ 分别为 $P B ､ P D$ 的中点，平面 $A E F$ 与棱 $P C$ 的交点为 $G$ .

(1)、求异面直线 $A E$ 与 $P F$ 所成角的大小；

(2)、求平面 $A E G F$ 与平面 $A B C D$ 所成锐二面角的大小；

(3)、求点 $G$ 的位置.

查看试题解析
21. 已知数列 ${a_{n}}$ 满足 $a_{n} = {\begin{array}{l} 2 (n = 1) \\ q a_{n - 1} + \frac{t}{a_{n - 1}} (q \geq 0 ， t \geq 0 ， q^{2} + t^{2} \neq 0 ， n \geq 2 ， n \in N) \end{array}$ .

(1)、当 $q > 1$ 时，求证：数列 ${a_{n}}$ 不可能是常数列；

(2)、若 $q t = 0$ ，求数列 ${a_{n}}$ 的前 $n$ 项的和；

(3)、当 $q = \frac{1}{2} ， t = 1$ 时，令 $b_{n} = \frac{2}{\sqrt{a_{n}^{2} - 2}} (n \geq 2 ， n \in N)$ ，判断对任意 $n \geq 2 ， n \in N$ ， $b_{n}$ 是否为正整数，请说明理由.

查看试题解析