2021-2022学年江苏省九年级上学期数学期末模拟试卷
试卷更新日期:2022-01-11 类型:期末考试
一、单选题
-
1. 一元二次方程x2﹣9=0的两根分别是a,b,且a>b,则2a﹣b的值为( )A、3 B、﹣3 C、6 D、92. 一组数据1,1,1,3,5,9,17,若加入一个整数a,一定不会发生变化的统计量是( )A、平均数 B、中位数 C、方差 D、众数3. 如图,在⊙O中, , ,则 的度数是( )
 A、 B、 C、 D、4. AD是△ABC的中线,E是AD上一点,AE= AD,BE的延长线交AC于F,则 的值为( )
A、 B、 C、 D、4. AD是△ABC的中线,E是AD上一点,AE= AD,BE的延长线交AC于F,则 的值为( ) A、 B、 C、 D、5. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1.与X轴的一个交点坐标为(-1,0),其图象如图所示:下列结论①4ac<b2. ②方程ax2+bx+c=0的两个根是x=-1,x=3. ③3a+c>0. ④当y>0时,x的取值范围是-1≤x<3. ⑤当x<0时,y随x的增大而增大,其中结论正确的个数是( )
A、 B、 C、 D、5. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1.与X轴的一个交点坐标为(-1,0),其图象如图所示:下列结论①4ac<b2. ②方程ax2+bx+c=0的两个根是x=-1,x=3. ③3a+c>0. ④当y>0时,x的取值范围是-1≤x<3. ⑤当x<0时,y随x的增大而增大,其中结论正确的个数是( ) A、1个 B、2个 C、3个 D、4个6. 如图, 为⊙O的内接四边形,且 平分 , 与⊙O相切.若 ,则 ( )
A、1个 B、2个 C、3个 D、4个6. 如图, 为⊙O的内接四边形,且 平分 , 与⊙O相切.若 ,则 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 若 ≠0,则 =.8. 已知α、β是方程x2+x﹣6=0的两根,则α2β+αβ= .9. 如图,大圆半径为6,小圆半径为2,在如图所示的圆形区域中,随机撒一把豆子,多次重复这个实验,若把“豆子落在小圆区域A中”记作事件W,请估计事件W的概率P(W)的值 .
 10. 将抛物线 平移,使它的顶点移到点P(-2,3),平移后新抛物线的表达式为 .11. 如图,已知圆锥的母线长OA=8,地面圆的半径r=2.若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是(结果保留根式).
10. 将抛物线 平移,使它的顶点移到点P(-2,3),平移后新抛物线的表达式为 .11. 如图,已知圆锥的母线长OA=8,地面圆的半径r=2.若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是(结果保留根式). 12. 如图,已知 是 的中位线, 是 的中点,连接 并延长与 交于点 ,若 ,则 的值是。
12. 如图,已知 是 的中位线, 是 的中点,连接 并延长与 交于点 ,若 ,则 的值是。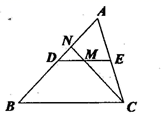 13. 已知二次函数 自变量x的部分取值和对应函数值y如下表:
13. 已知二次函数 自变量x的部分取值和对应函数值y如下表:…
-2
-1
0
1
2
3
…
…
5
0
-3
-4
-3
0
…
则在实数范围内能使 成立的x的取值范围是.
14. 如图,A、B、C是⊙O上的三点,且四边形OABC是菱形.若点D是圆上异于A、B、C的另一点,则∠ADC的度数是 .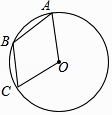 15. 二次函数 图象 轴上方的部分沿 轴翻折到 轴下方,图象的其余部分保持不变,翻折后的图象与原图象 轴下方的部分组成一个“ ”形状的新图象,若直线 与该新图象有两个公共点,则 的取值范围为.16. 如图,已知直线 与x轴、y轴分别交于A、B两点,P是以 为圆心,1为半径的圆上一动点,连接 、 ,当 的面积最大时,点P的坐标为 .
15. 二次函数 图象 轴上方的部分沿 轴翻折到 轴下方,图象的其余部分保持不变,翻折后的图象与原图象 轴下方的部分组成一个“ ”形状的新图象,若直线 与该新图象有两个公共点,则 的取值范围为.16. 如图,已知直线 与x轴、y轴分别交于A、B两点,P是以 为圆心,1为半径的圆上一动点,连接 、 ,当 的面积最大时,点P的坐标为 .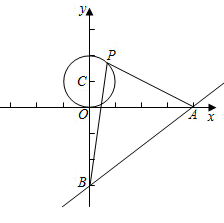
三、解答题
-
17. 解方程:(1)、(2)、18. 如图,已知 ,求证:△ABD∽△ACE
 19. 已知二次函数 (m是常数)(1)、求证:不论m为何值,该函数的图象与x轴没有公共点;(2)、把该函数的图象沿x轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?20. 袋中装有大小相同的2个红球和2个绿球.
19. 已知二次函数 (m是常数)(1)、求证:不论m为何值,该函数的图象与x轴没有公共点;(2)、把该函数的图象沿x轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?20. 袋中装有大小相同的2个红球和2个绿球.
(1)、先从袋中摸出1个球后放回,混合均匀后再摸出1个球.①求第一次摸到绿球,第二次摸到红球的概率;
②求两次摸到的球中有1个绿球和1个红球的概率;
(2)、先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
21. 希望中学八年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩较好的甲班和乙班5名学生的比赛成绩(单位:个)1号
2号
3号
4号
5号
总数
甲班
100
98
110
89
103
500
乙班
89
100
95
119
97
500
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)、求两班比赛数据的中位数;(2)、计算两班比赛数据的方差,并比较哪一个小;(3)、根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.22. 在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.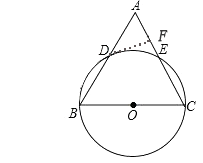 (1)、求证:DF是⊙O的切线;(2)、分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.
(1)、求证:DF是⊙O的切线;(2)、分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.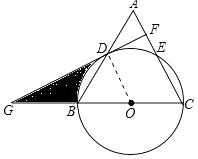 23. 已知二次函数 的图象经过点(1,0)和(0,2).(1)、求b,c的值;(2)、当 时,求 的取值范围;(3)、已经点P(m,n)在该函数的图象上,且 ,求点P的坐标.24. 已知四边形 ,用无刻度的直尺和圆规完成下列作图.(保留作图痕迹,不写作法)
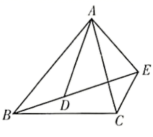
23. 已知二次函数 的图象经过点(1,0)和(0,2).(1)、求b,c的值;(2)、当 时,求 的取值范围;(3)、已经点P(m,n)在该函数的图象上,且 ,求点P的坐标.24. 已知四边形 ,用无刻度的直尺和圆规完成下列作图.(保留作图痕迹,不写作法) (1)、如图①,连接 ,在 边上作出一个点M,使得 ;(2)、如图②,在 边上作出一个点N,使得 .25. 如图,已知 是△ 的外角 的平分线,交 的延长线于点 ,延长 交△ 的外接圆于点 ,连接 , .
(1)、如图①,连接 ,在 边上作出一个点M,使得 ;(2)、如图②,在 边上作出一个点N,使得 .25. 如图,已知 是△ 的外角 的平分线,交 的延长线于点 ,延长 交△ 的外接圆于点 ,连接 , . (1)、求证: .(2)、已知 ,若 是△ 外接圆的直径, ,求 的长.26. 如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.
(1)、求证: .(2)、已知 ,若 是△ 外接圆的直径, ,求 的长.26. 如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.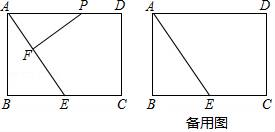 (1)、求证:△PFA∽△ABE;(2)、当点P在线段AD上运动时,设PA=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;(3)、探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出x满足的条件:.27. 在平面直角坐标系xOy中,规定:抛物线y=a(x﹣h)2+k的伴随直线为y=a(x﹣h)+k.例如:抛物线y=2(x+1)2﹣3的伴随直线为y=2(x+1)﹣3,即y=2x﹣1.(1)、在上面规定下,抛物线y=(x+1)2﹣4的顶点坐标为 , 伴随直线为 , 抛物线y=(x+1)2﹣4与其伴随直线的交点坐标为和;(2)、如图,顶点在第一象限的抛物线y=m(x﹣1)2﹣4m与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
(1)、求证:△PFA∽△ABE;(2)、当点P在线段AD上运动时,设PA=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;(3)、探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出x满足的条件:.27. 在平面直角坐标系xOy中,规定:抛物线y=a(x﹣h)2+k的伴随直线为y=a(x﹣h)+k.例如:抛物线y=2(x+1)2﹣3的伴随直线为y=2(x+1)﹣3,即y=2x﹣1.(1)、在上面规定下,抛物线y=(x+1)2﹣4的顶点坐标为 , 伴随直线为 , 抛物线y=(x+1)2﹣4与其伴随直线的交点坐标为和;(2)、如图,顶点在第一象限的抛物线y=m(x﹣1)2﹣4m与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.①若∠CAB=90°,求m的值;
②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值 时,求m的值.
