黑龙江省齐齐哈尔市富裕县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-10 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程x²﹣16＝0的根是（　　）

A、4 B、﹣4 C、±4 D、16

查看试题解析
2. 下列图形中，既是中心对称图形又是轴对称图形的有几个（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列事件是必然事件的是（　　）

A、抛一枚硬币正面朝上 B、若a为实数，则a²≥0 C、某运动员射击一次击中靶心 D、明天一定是晴天

查看试题解析
4. 方程kx²﹣6x+1＝0有实数根，则k的取值范围是（　　）

A、k≤9 B、k≤9且k≠0 C、k≠0 D、k＞9

查看试题解析
5. 把抛物线y＝x²向右平移1个单位长度，再向上平移3个单位长度，得到的抛物线解析式是（　　）

A、y＝（x+1）²+3 B、y＝（x+1）²﹣3 C、y＝（x﹣1）²﹣3 D、y＝（x﹣1）²+3

查看试题解析
6. 如图所示，以AB为直径的半圆，绕点B顺时针旋转60°，点A旋转到点A′，且AB＝4，则图中阴影部分的面积是（　　）

A、 $\frac{π}{3}$ B、 $\frac{8 π}{3}$ C、8 D、 $\frac{π}{6}$

查看试题解析
7. 如图，四边形ABCD内接于⊙O，若∠ADC＝140°，则∠AOC的度数为（　　）

A、25° B、80° C、130° D、100°

查看试题解析
8. 如图所示，圆锥的底面圆的半径为5，母线长为30，一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到A点的最短路程是（　　）

A、8 B、 $10 \sqrt{2}$ C、30 D、 $20 \sqrt{2}$

查看试题解析
9. 如图，点D是等边△ABC内一点，AD＝3，BD＝3，CD＝ $3 \sqrt{2}$ ， △ACE是由△ABD绕点A逆时针旋转得到的，则∠ADC的度数是（　　）

A、40° B、45° C、105° D、55°

查看试题解析
10. 如图，二次函数y＝ax²+bx+c（a≠0）图象的一部分，对称轴为 $x = \frac{1}{2}$ ，且经过点（2，0）．下列说法：①abc＜0，②a﹣b＝0，③4a+2b+c＜0，④若（﹣2，y₁） $(\frac{5}{2} ， y_{2})$ 是抛物线上的两点，则y₁＜y₂ ，其中说法正确的是（　　）

A、①④ B、③④ C、①③④ D、①②

查看试题解析

二、填空题

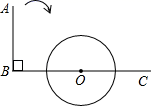
11. 在函数y= $\sqrt{x + 3}$ + $\frac{1}{x^{2}}$ 中，自变量x的取值范围是．

查看试题解析
12. 抛物线y＝x²﹣2x﹣3的顶点坐标是.

查看试题解析
13. 智能音箱是市场上最火的智能产品之一，某商户一月份销售了100个智能音箱，三月份比一月份多销售44个，设该公司二、三月销量的月平均增长率为x，则可列方程为．

查看试题解析
14. 一个不透明的布袋里装有3个小球（只有颜色不同），其中2个是红球，1个是白球从中任意摸出一个球（不放回袋里）再从中随机摸出一球，则摸出的两个球都是红球的概率是．

查看试题解析
15. 如图，∠ABC＝90°，O为射线BC上点，以点O为圆心， $\frac{1}{2}$ BO长为半径作⊙O，当射线BA绕点B按顺时针方向旋转度时与⊙O相切．

查看试题解析
16. 圆锥的母线长为5，高为3，侧面积为．

查看试题解析
17. 在平面直角坐标系中，若干个边长为1个单位长度的等边三角形，按如图中的规律摆放．点P从原点O出发，以每秒1个单位长度的速度沿着等边三角形的边“ $O A_{1} \to A_{1} A_{2} \to A_{2} A_{3} \to A_{3} A_{4} \to A_{4} A_{5} ⋯$ ”的路线运动，设第n秒运动到点 $P_{n}$ （n为正整数），则点 $P_{2021}$ 的坐标是．

查看试题解析

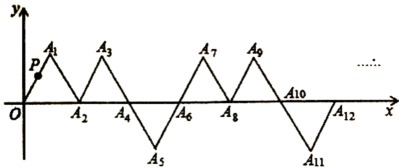
三、解答题

18. 计算 $(\frac{1}{2})^{- 1} + \sqrt{121} - (π - 1)^{0} - | π - 11 |$ ．

查看试题解析
19.

(1)、请你用公式法解方程3x²﹣5x﹣8＝0；

(2)、请你用因式分解法解方程x²+4x+3＝0．

查看试题解析
20. 如图，已知⊙O的直径为AB，AC⊥AB于点A，BC与⊙O相交于点D，在AC上取一点E，使得ED=EA．

(1)、求证：ED是⊙O的切线．

(2)、当OA=3，AE=4时，求BC的长度．

查看试题解析
21. 在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球各一个，现在有甲，乙，丙三个同学，甲先从纸箱里摸取一个小球，记下颜色后放回，乙再摸取，记下颜色后放回，最后丙摸取，记下颜色．

(1)、请同学们利用树状图计算三个人摸取的小球颜色相同的概率．

(2)、按照以上的摸取方式，如果想使总的可能结果超过100种，至少需要几个人？（直接写出结论即可）

查看试题解析
22. 某商场销售一批衬衫，进货价为每件30元，按每件50元出售，一个月内可售出500件．已知这种衬衫每件涨价1元，其销售量要减少10件，

(1)、要在一个月内赚取12000元的利润，同时为了减少库存，售价应定为每件多少元？

(2)、要想一个月内获得的利润最大，该商场应当如何定价销售？

查看试题解析
23. 综合与实践

(1)、如图1，在正方形ABCD中，点M、N分别在AD、CD上，若∠MBN＝45°，则MN，AM，CN的数量关系为．

(2)、如图2，在四边形ABCD中，BC∥AD，AB＝BC，∠A+∠C＝180°，点M、N分别在AD、CD上，若∠MBN＝ $\frac{1}{2}$ ∠ABC，试探索线段MN、AM、CN有怎样的数量关系？请写出猜想，并给予证明．

(3)、如图3，在四边形ABCD中，AB＝BC，∠ABC+∠ADC＝180°，点M、N分别在DA、CD的延长线上，若∠MBN＝ $\frac{1}{2}$ ∠ABC，试探究线段MN、AM、CN的数量关系为．

查看试题解析
24. 如图，在平面直角坐标系中，抛物线y＝ax²+4x+c（a≠0）与x轴交于点A、B，与y轴交于点C，连接BC，OA＝1，对称轴为x＝2，点D为抛物线的顶点．

(1)、求抛物线的解析式；

(2)、抛物线上C ， D两点之间的距离是；

(3)、点E是第一象限内抛物线上的动点，连接BE和CE ．求△BCE面积的最大值；

(4)、平面内存在点Q ，使以点B、C、D、Q为顶点的四边形为平行四边形，请直接写出点Q的坐标．

查看试题解析