吉林省长春市农安县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-10 类型:期末考试
一、单选题
-
1. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、2. 下列说法正确的是( )A、“买中奖率为的奖券10张,中奖”是必然事件 B、“汽车累积行驶 , 出现一次故障”是随机事件 C、襄阳气象局预报说“明天的降水概率为70%”,意味着襄阳明天一定下雨 D、若两组数据的平均数相同,则方差大的更稳定3. 下列二次根式中,与是同类二次根式的是( )A、 B、 C、 D、4. 如图,某停车场入口的栏杆 , 从水平位置绕点O旋转到的位置,已知的长为5米.若栏杆的旋转角 , 则栏杆A端升高的高度为( )
 A、米 B、米 C、米 D、米5. 如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( )
A、米 B、米 C、米 D、米5. 如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( )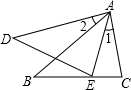 A、∠C=∠AED B、∠B=∠D C、 D、6. 已知二次函数的图象经过原点,则a的值为( )A、0或2 B、0 C、2 D、无法确定7. 由二次函数可知( )A、其图象的开口向上 B、其顶点坐标为 C、其图象的对称轴为直线 D、当时,y随x的增大而增大8. 如图,已知D、E分别为、上的两点,且DEBC, , 则的长为( )
A、∠C=∠AED B、∠B=∠D C、 D、6. 已知二次函数的图象经过原点,则a的值为( )A、0或2 B、0 C、2 D、无法确定7. 由二次函数可知( )A、其图象的开口向上 B、其顶点坐标为 C、其图象的对称轴为直线 D、当时,y随x的增大而增大8. 如图,已知D、E分别为、上的两点,且DEBC, , 则的长为( )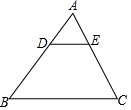 A、6 B、16 C、8 D、12
A、6 B、16 C、8 D、12二、填空题
-
9. 若在实数范围内有意义,则x的取值范围是 .10. 若 , 则 .11. 如图,四边形与四边形位似,其位似中心为点O,且 , 则 .
 12. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为660平方米,则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为 .
12. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为660平方米,则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为 .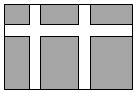 13. 如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m.
13. 如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m. 14. 如图,在平面直角坐标系中,正方形的顶点A在y轴的负半轴上,点C在x轴的负半轴上,抛物线的顶点为E,且经过点A、B,若△为等腰直角三角形,则a的值是 .
14. 如图,在平面直角坐标系中,正方形的顶点A在y轴的负半轴上,点C在x轴的负半轴上,抛物线的顶点为E,且经过点A、B,若△为等腰直角三角形,则a的值是 .
三、解答题
-
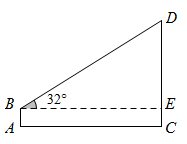
15. 计算:(1)、(2)、16. 如图,小明为了测量学校旗杆的高度,在地面离旗杆底部C处22米的A处放置高度为1.8米的测角仪 , 测得旗杆顶端D的仰角为 . 求旗杆的高度 . (结果精确到0.1米)(参考数据:)
 17. 现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球.其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球.小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小华获胜;若颜色不同,则小林获胜.请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平,如果不公平,谁获胜的机会大.18. 2020年,受新冠肺炎疫情影响.口罩紧缺,某网店购进了一批口罩,二月份销售了256袋,三、四月该口罩十份畅销,销售量持续走高,四月份的销售量达到400袋.(1)、求三、四这两个月销售量的月平均增长率;(2)、如果继续按照相同的增长率增长,那么五月份的销售量会达到多少袋口罩?19. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A、B、C、D均在格点上在图②、图③中,只用无刻度的直尺,在给定的正方形网格中,按要求画图,保留作图痕迹,不要求写出画法.
17. 现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球.其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球.小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小华获胜;若颜色不同,则小林获胜.请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平,如果不公平,谁获胜的机会大.18. 2020年,受新冠肺炎疫情影响.口罩紧缺,某网店购进了一批口罩,二月份销售了256袋,三、四月该口罩十份畅销,销售量持续走高,四月份的销售量达到400袋.(1)、求三、四这两个月销售量的月平均增长率;(2)、如果继续按照相同的增长率增长,那么五月份的销售量会达到多少袋口罩?19. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A、B、C、D均在格点上在图②、图③中,只用无刻度的直尺,在给定的正方形网格中,按要求画图,保留作图痕迹,不要求写出画法.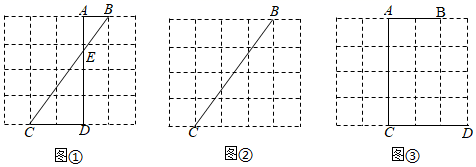 (1)、如图①, .(2)、如图②,在上找一点F,使 .(3)、如图③,在上找一点M,连结、 , 使 .20. 如图,中,于点D.
(1)、如图①, .(2)、如图②,在上找一点F,使 .(3)、如图③,在上找一点M,连结、 , 使 .20. 如图,中,于点D.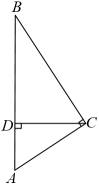 (1)、求证:;(2)、如果 , 求的长.21. 已知关于x的一元二次方程x2﹣mx﹣2=0…①(1)、若x=﹣1是方程①的一个根,求m的值和方程①的另一根;(2)、对于任意实数m , 判断方程①的根的情况,并说明理由.22. (教材呈现)下图是华师版九年级上册数学教材第78页的部分内容.
(1)、求证:;(2)、如果 , 求的长.21. 已知关于x的一元二次方程x2﹣mx﹣2=0…①(1)、若x=﹣1是方程①的一个根,求m的值和方程①的另一根;(2)、对于任意实数m , 判断方程①的根的情况,并说明理由.22. (教材呈现)下图是华师版九年级上册数学教材第78页的部分内容.例2 如图:在中,D、E分别是边、的中点, 、相交于点G.求证: .
证明:连接 .
 (1)、请根据教材提示,结合图①,写出完整的证明过程.(2)、(结论应用)如图②,在中,D、F分别是边、的中点,、相交于点G,GEAC交于点E,GHAB交于点H,则与的面积的比值为 .
(1)、请根据教材提示,结合图①,写出完整的证明过程.(2)、(结论应用)如图②,在中,D、F分别是边、的中点,、相交于点G,GEAC交于点E,GHAB交于点H,则与的面积的比值为 . 23. 如图,在中, , , . 动点P从点A出发,沿以每秒5个单位长度的速度向终点B运动.当点P不与点A重合时,过点P作于点D、以 , 为边作 . 设点P的运动时间为t秒.
23. 如图,在中, , , . 动点P从点A出发,沿以每秒5个单位长度的速度向终点B运动.当点P不与点A重合时,过点P作于点D、以 , 为边作 . 设点P的运动时间为t秒. (1)、线段的长为 . (用含t的代数式表示).(2)、当点E落在边上时,求t的值.(3)、连结 , 当时,求t的值.(4)、若线段的中点为Q,当点Q落在一边垂直平分线上时,直接写出t的值.24. 在平面直角坐标系中,点A的坐标为 , 过点A作y轴的平行线交二次函数的图象于点B.
(1)、线段的长为 . (用含t的代数式表示).(2)、当点E落在边上时,求t的值.(3)、连结 , 当时,求t的值.(4)、若线段的中点为Q,当点Q落在一边垂直平分线上时,直接写出t的值.24. 在平面直角坐标系中,点A的坐标为 , 过点A作y轴的平行线交二次函数的图象于点B. (1)、点B的纵坐标为(用含m的代数式表示);(2)、当点A落在二次函数的图象上时,求m的值;(3)、当时,若 . 求m的值;(4)、当线段的长度随m的增大而增大时,直接写出m的取值范围.
(1)、点B的纵坐标为(用含m的代数式表示);(2)、当点A落在二次函数的图象上时,求m的值;(3)、当时,若 . 求m的值;(4)、当线段的长度随m的增大而增大时,直接写出m的取值范围.