吉林省白城市通榆县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-10 类型：期末考试

进入出卷网下载

一、单选题

1. 在一元二次方程x²﹣2x﹣1＝0中，常数项是（　　）

A、1 B、﹣2 C、﹣1 D、0

查看试题解析
2. 如图，在下面的扑克牌中，牌面是中心对称图形的有（）

A、2张 B、3张 C、4张 D、5张

查看试题解析
3. 抛物线 $y = {(x - 2)}^{2} + 2$ 的顶点坐标是（）．

A、 $(- 2 ， 2)$ B、 $(2 ， - 2)$ C、 $(2 ， 2)$ D、 $(- 2 ， - 2)$

查看试题解析
4. 某超市一月份的营业额为36万元，三月份的营业额为48万元，设每月的平均增长率为x，则可列方程为（）

A、48（1﹣x）²=36 B、48（1+x）²=36 C、36（1﹣x）²=48 D、36（1+x）²=48

查看试题解析
5. 在 Rt△ABC 中，∠C＝90°，BC＝3cm，AC＝4cm，以点C 为圆心，以2.5cm 为半径画圆，则⊙C与直线AB的位置关系是（）

A、相交 B、相切 C、相离 D、不能确定

查看试题解析
6. 当ab>0时，y=ax²与y=ax+b的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 点A（﹣2，3）关于原点对称的点的坐标是．

查看试题解析
8. 不透明袋子中装有9个球，其中有2个红球、3个绿球和4个蓝球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是红球的概率是.

查看试题解析
9. 将抛物线 $y = 2 x^{2}$ 向右平移4个单位长度，再向上平移1个单位长度，得到抛物线对应的解析式为．

查看试题解析
10. 工程上常用钢珠来测量零件上小圆孔的宽口，假设钢珠的直径是10mm，测得钢珠顶端离零件表面的距离为8mm，如图所示，则这个小圆孔的宽口AB的长度为mm．

查看试题解析
11. 如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AC＝ $\sqrt{3}$ ，∠B＝60°，则CD的长为．

查看试题解析
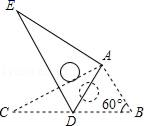12. 小明设计了一个魔术盒，当任意实数对(a，b)进入其中时，会得到一个新的实数a²＋2b－3.例如把(2，－5)放入其中就会得到2²＋2×(－5)－3＝－9.现将实数对(m，－3m)放入其中，得到实数4，则m＝.

查看试题解析
13. 如图，PA、PB分别切⊙O于点A、B，点E是⊙O上一点，且∠AEB=60°，则∠P=度．

查看试题解析
14. 如图，菱形ABCD的三个顶点在二次函数 $y = a x^{2} - 2 a x + \frac{3}{2} (a < 0)$ 的图象上，点A、B分别是该抛物线的顶点和抛物线与y轴的交点，则点D的坐标为．

查看试题解析

三、解答题

15. 用配方法解方程2x²﹣4x﹣1＝0．

查看试题解析
16. 经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，这三种可能性大小相同，现在两辆汽车经过这个十字路口．请用“树形图”或“列表法”求这两辆汽车都向左转的概率．

查看试题解析
17. 关于x的方程x²﹣（k+1）x+k＝0有两个相等的实数根，求k的值．

查看试题解析
18. 如图是一圆锥，底面圆的半径为AO＝1，高PO $= \sqrt{3}$ ．求侧面展开图面积．

查看试题解析
19. 如图，△ABC三个顶点的坐标分别为A（2，4），B（1，1），C（4，3）．

(1)、请画出△ABC关于x轴对称的△A₁B₁C₁ ，并写出点A₁的坐标．

(2)、请画出△ABC绕点B逆时针旋转90°后的△A₂BC₂ ，并写出点A₂的坐标．

查看试题解析
20. 今年我县在老旧小区改造方面取得了巨大成就，人居环境得到了很大改善．某小区规划在长16m，宽9m的矩形场地ABCD上，修建同样宽的小路，使其中的小路分别与AB和AD平行，其余部分种草．如果使草坪的总面积为112m² ，设小路宽为xm．如图所示，施工人员设计了两种方案，请你通过计算帮助选择一种数据准确且更容易测量和实施的方案．

查看试题解析
21. 如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．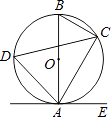

(1)、求∠ABC的度数；

(2)、求证：AE是⊙O的切线；

(3)、当BC=4时，求劣弧AC的长．

查看试题解析
22. 我市“利民快餐店”试销某种套餐，试销一段时间后发现，每份套餐的成本为5元，该店每天固定支出费用为600元（不含套餐成本）．若每份售价不超过10元，每天可销售400份；若每份售价超过10元，每提高1元，每天的销售量就减少40份．为了便于结算，每份套餐的售价x（元）取整数，用y（元）表示该店日纯收入．（日纯收入=每天的销售额﹣套餐成本﹣每天固定支出）

(1)、若每份套餐售价不超过10元．
①试写出y与x的函数关系式；
②若要使该店每天的纯收入不少于800元，则每份套餐的售价应不低于多少元？

(2)、该店既要吸引顾客，使每天销售量较大，又要有较高的日纯收入．按此要求，每份套餐的售价应定为多少元？此时日纯收入为多少元？

查看试题解析
23. 已知∠AOB＝90°，在∠AOB的平分线OM上有一点C，将一个三角板的直角顶点与C重合，它的两条直角边分别与OA，OB(或它们的反向延长线)相交于点D，E.
当三角板绕点C旋转到CD与OA垂直时(如图①)，易证：OD＋OE＝ $\sqrt{2}$ OC；
当三角板绕点C旋转到CD与OA不垂直时，即在图②，图③这两种情况下，上述结论是否仍然成立？若成立，请给予证明：若不成立，线段OD，OE，OC之间又有怎样的数量关系？请写出你的猜想，不需证明．

查看试题解析
24. 已知，m，n是一元二次方程x²+4x+3=0的两个实数根，且|m|＜|n|，抛物线y=x²+bx+c的图象经过点A（m，0），B（0，n），如图所示．

(1)、求这个抛物线的解析式；

(2)、设（1）中的抛物线与x轴的另一个交点为C，抛物线的顶点为D，求出点C，D的坐标，并判断△BCD的形状；

(3)、点P是直线BC上的一个动点（点P不与点B和点C重合），过点P作x轴的垂线，交抛物线于点M，点Q在直线BC上，距离点P为 $\sqrt{2}$ 个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．

查看试题解析