黑龙江省双鸭山市集贤县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-10 类型：期末考试

进入出卷网下载

一、单选题

1. 若关于x的一元二次方程 $a x^{2} + 4 x - 1 = 0$ 有实数根，则a的取值范围是（）

A、 $a \geq 4$ B、 $a \leq - 4$ C、 $a > - 4$ 且 $a \neq 0$ D、 $a \geq - 4$ 且 $a \neq 0$

查看试题解析
2. 抛物线 $y = 3 {(x - 3)}^{2} + 4$ 顶点坐标是（）

A、 $(- 3 ， 4)$ B、 $(3 ， 4)$ C、 $(4 ， 3)$ D、 $(- 4 ， 3)$

查看试题解析
3. 某口罩生产厂家2019年产量为100万个，为支持防疫工作，加大生产，2021年口罩产量为196万个，求该口罩厂家产量的年平均增长率．设该口罩厂家产量的年平均增长率为x，则根据题意可列方程为（　　）

A、100x²＝196 B、100（1﹣x）²＝196 C、196（1＋x）²＝100 D、100（1＋x）²＝196

查看试题解析
4. 下列图形中，不是中心对称图形是（）

A、 B、 C、 D、

查看试题解析
5. 将抛物线 $y = - 2 x^{2} + 1$ 向右平移1个单位，再向下平移2个单位后所得到的抛物线为（）

A、 $y = - 2 {(x + 1)}^{2} - 1$ B、 $y = - 2 {(x - 1)}^{2} + 3$ C、 $y = - 2 {(x - 1)}^{2} - 1$ D、 $y = - 2 {(x + 1)}^{2} + 3$

查看试题解析
6. 如图，Rt $△$ ABC中，∠C＝90°，AC＝4，BC＝3，以B点为中心，将 $△$ ABC旋转至 $△$ DBE，使E点恰好在AB上，则AE的长为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如果⊙O的半径为6，线段OP的长为3，则点P与⊙O的位置关系是（　　）

A、点P在⊙O上 B、点P在⊙O内 C、点P在⊙O外 D、无法确定

查看试题解析
8. 有一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其它完全相同。小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%，则口袋中白色球的个数很可能是（）

A、6 B、16 C、18 D、24

查看试题解析
9. 一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合，且与边AB、CD相交于G、H（如图）.图中阴影部分的面积记为S，三条线段GB、BC、CH的长度之和记为l，大正六边形在绕点O旋转过程中，下列说法正确的是（）

A、S变化，l不变 B、S不变，l变化 C、S变化，l变化 D、S与l均不变

查看试题解析
10. 二次函数y=ax²+bx+c的图象如图所示，对称轴是x=－1．有以下结论：①abc>0，②4ac＜b² ， ③2a+b=0，④a－b+c>2，其中正确的结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 关于x的方程 $(m - 2) x^{m^{2} - 2} - 3 x + 1 = 0$ 是一元二次方程，则m= ．

查看试题解析
12. 如果一元二次方程 $x^{2} - 2 x - 2 = 0$ 的两根分别为 $x_{1}$ ， $x_{2}$ ，那么 $x_{1} + x_{2} =$ .

查看试题解析
13. 已知抛物线y=(m－1) x²开口向下，则m的取值范围是.

查看试题解析
14. 一个不透明的口袋中装有标号为1、2、3的三个小球，这些小球除标号外完全相同，随机摸出1个小球，然后把小球重新放回口袋并摇匀，再随机摸出1个小球，那么两次摸出小球上的数字之和是偶数的概率是．

查看试题解析
15. 发射一枚炮弹，经 $x$ 秒后的高度为 $y$ 米，且时间与高度的关系为 $y = a x^{2} + b x + c (a \neq 0)$ ．若此炮弹在第7秒与第15秒时的高度相等，则第秒时炮弹位置达到最高．

查看试题解析
16. 如图，在△ABC中，∠C＝36°，将△ABC绕点A按逆时针方向旋转得到△AB′C′．若点B′恰好落在BC边上，且AB′＝CB′，则旋转角为度．

查看试题解析
17. 如图，已知点A的坐标是 $(- 2 \sqrt{3}$ ， $2)$ ，点B的坐标是 $(- 1$ ， $- \sqrt{3})$ ，菱形 $A B C D$ 的对角线交于坐标原点O，则点D的坐标是．

查看试题解析
18. 如图，在 $⊙ O$ 中， $A B$ 是直径，弦 $A C$ 的长为5cm，点D在圆上，且 $∠ A D C = 30 °$ ，则 $⊙ O$ 的半径为．

查看试题解析
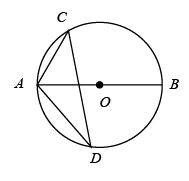19. ⊙O的半径为2，弦BC＝2 $\sqrt{3}$ ，点A是⊙O上一点，且AB＝AC，直线AO与BC交于点D，则AD的长为．

查看试题解析
20. 用半径为30，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为.

查看试题解析

三、解答题

21. “航天知识竞赛”活动中，获得“小宇航员”称号的小明得到了A、B、C三枚纪念章．如图，A、B、C三枚纪念章正面上分别印有“嫦娥五号”、“天问一号”和“天宫一号”的图案．三枚纪念章除正面图案不同外，其余均相同，小明将这三枚纪念章背面朝上放在桌面上，然后从中随机选取一枚，记下图案并放回，重新洗匀后再从中随机抽取一张．请用画树状图（或列表）的方法，求小明两次抽到图案上至少有一张印有“嫦娥五号”图案的概率．

查看试题解析
22. 如图， $△ A B C$ 三个顶点的坐标分别为 $A (2 ， 4)$ ， $B (1 ， 1)$ ， $C (4 ， 3)$ ．

⑴请画出 $△ A B C$ 关于原点对称的图形 $△ A_{1} B_{1} C_{1}$ ；

⑵请画出 $△ A B C$ 绕原点O按逆时针方向旋转90°后的图形 $△ A_{2} B_{2} C_{2}$ ；

⑶求线段 $C C_{2}$ 的长．

查看试题解析
23. 如图是宽为20m，长为32m的矩形耕地，要修筑同样宽的三条道路（互相垂直），把耕地分成六块大小相等的试验地，要使试验地的面积为570m² ，问：道路宽为多少米？

查看试题解析
24. 如图，抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 与x轴交于点 $A (1 ， 0)$ 和点 $B (- 3 ， 0)$ ，与y轴交于点C，抛物线的对称轴与抛物线交于点D．

(1)、求抛物线的解析式；

(2)、点P是抛物线对称轴上的一个动点，连接AP、PC，请直接写出使 $A P + P C$ 值最小的点P的坐标．

查看试题解析
25. 如图，点O是等边三角形ABC内的一点，∠BOC=150°，将△BOC绕点C按逆时针旋转得到△ADC，连接OD，OA．

(1)、求∠ODC的度数；

(2)、若OB=2，OC=3，求AO的长．

查看试题解析
26. 如图， $A B$ 是 $⊙ O$ 的直径，点P在 $A B$ 的延长线上，弦 $C E$ 交 $A B$ 于点D．连结 $O E$ 、 $A C$ ，已知 $∠ P O E = 2 ∠ C A B$ ， $∠ P = ∠ E$ ．

(1)、求证： $C E ⊥ A B$ ；

(2)、求证： $P C$ 是 $⊙ O$ 的切线．

查看试题解析
27. 如图，有长为24m的篱笆，现一面利用墙（墙的最大可用长度a为10m），设花圃的宽AB为xm，面积为S $m^{2}$ ．

(1)、求S与x的函数关系式及x值的取值范围；

(2)、要围成面积为45 $m^{2}$ 的花圃，AB的长是多少米？

(3)、当AB的长是多少米时，围成的花圃的面积最大？（结果保留两位小数）

查看试题解析
28. 如图，Rt△ABC中，∠C＝90°，AC＝6，BC＝8，动点P、Q分别从A、C两点同时出发，P点沿边AC向C以每秒3个单位长度的速度运动，Q点沿边BC向B以每秒4个单位长度的速度运动，当P、Q到达终点C、B时，运动停止，设运动时间为t（s）．

(1)、①当运动停止时，t的值为；
②设P、C之间的距离为y，则y与t满足关系（填“正比例函数”、“一次函数”或“二次函数”）；

(2)、设△PCQ的面积为S．
①求S的表达式（用含t的式子表示）；
②求当t为何值时，S取得最大值，这个最大值是多少？

查看试题解析