吉林省长春市农安县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-10 类型:期末考试
一、单选题
-
1. 的算术平方根是( )A、3 B、﹣3 C、﹣9 D、92. 下列运算正确的是( )A、a4•a2=a8 B、(2a3)2=4a6 C、(ab)6÷(ab)2=a3b3 D、(a+b)(a﹣b)=a2+b23. 下列各式从左到右的变形属于因式分解的是( )A、(x+2)(x﹣3)=x2﹣x﹣6 B、6xy=2x•3y C、x2+2x+1=x(x+2)+1 D、x2﹣9=(x﹣3)(x+3)4. 下列四组线段中,可以构成直角三角形的是( )A、4,5,6 B、2,3,4 C、 ,3,4 D、1, ,35. (+m)与(+3)的乘积中不含的一次项,则m的值为( )A、-3 B、3 C、0 D、16. 如图,AB=AC,AD=AE,∠A=105°,∠D=25°,则∠ABE等于( )
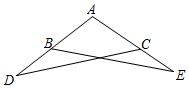 A、65° B、60° C、55° D、50°7. 下列选项中的尺规作图,能推出PA=PC的是( )A、
A、65° B、60° C、55° D、50°7. 下列选项中的尺规作图,能推出PA=PC的是( )A、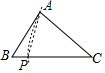 B、
B、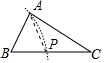 C、
C、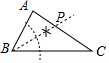 D、
D、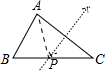 8. 如果等腰三角形的两边长分别为2和5,则它的周长为( )
8. 如果等腰三角形的两边长分别为2和5,则它的周长为( )
A、9 B、7 C、12 D、9或129. 为了解中学300名男生的身高情况,随机抽取若干名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图).估计该校男生的身高在169.5cm~174.5cm之间的人数有( )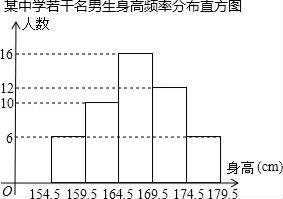 A、12 B、48 C、72 D、9610. 如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
A、12 B、48 C、72 D、9610. 如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )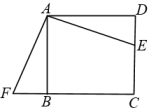 A、4 B、8 C、16 D、无法计算
A、4 B、8 C、16 D、无法计算二、填空题
-
11. 实数8的立方根是 .12. 因式分解:x2y4﹣x4y2= .13. 化简:(﹣x)2(﹣x)3= .14. 代数式x2﹣kx+9是一个完全平方式,则k的值是 .15. 已知ab,a,b为两个连续的自然数,则a+b= .16. 命题“两直线平行,同位角相等”的逆命题是命题.(填“真”或“假”)17. 如图,在△ABC中,AB=AC,BD是△ABC的一条角平分线,若∠A =36°,则∠BDC的度数为 .
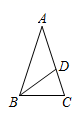 18. 如图,在一只底面半径为3cm,高为8cm的圆柱体状水杯中放入一支13cm长的吸管,那么这支吸管露出杯口的长度是 .
18. 如图,在一只底面半径为3cm,高为8cm的圆柱体状水杯中放入一支13cm长的吸管,那么这支吸管露出杯口的长度是 .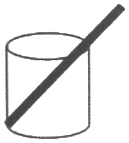 19. 如图所示,BD是∠ABC的平分线,DE⊥AB于点E,AB=36cm,BC=24cm,S△ABC=144cm,则DE的长是 .
19. 如图所示,BD是∠ABC的平分线,DE⊥AB于点E,AB=36cm,BC=24cm,S△ABC=144cm,则DE的长是 .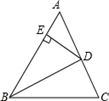 20. 如图,在和中,点在同一直线上, , 请添加一个条件,使 , 这个添加的条件可以是(只需写一个,不添加辅助线),并证明.
20. 如图,在和中,点在同一直线上, , 请添加一个条件,使 , 这个添加的条件可以是(只需写一个,不添加辅助线),并证明.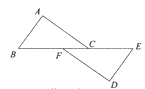
三、解答题
-
21. 计算: .22. 先化简,再求值: ,其中 .23. 如图, 中,D为BC边上的一点,AD=AC,以线段AD为边作 ,使得AE=AB,∠BAE=∠CAD.求证:DE=CB.
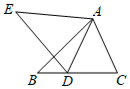 24. 如图,一架长为5米的梯子 斜靠在与地面 垂直的墙 上,梯子底端距离墙ON有3米.
24. 如图,一架长为5米的梯子 斜靠在与地面 垂直的墙 上,梯子底端距离墙ON有3米.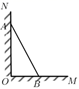 (1)、求梯子顶端与地面的距离 的长.(2)、若梯子顶点 下滑1米到 点,求梯子的底端向右滑到 的距离.25. 如图,在4×4的正方形网格中,每个小正方形的边长均为1.
(1)、求梯子顶端与地面的距离 的长.(2)、若梯子顶点 下滑1米到 点,求梯子的底端向右滑到 的距离.25. 如图,在4×4的正方形网格中,每个小正方形的边长均为1. (1)、请在所给网格中画一个边长分别为 , , 的三角形;(2)、此三角形的面积是 .26. 为了解我市的空气质量情况,某环保兴趣小组从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
(1)、请在所给网格中画一个边长分别为 , , 的三角形;(2)、此三角形的面积是 .26. 为了解我市的空气质量情况,某环保兴趣小组从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).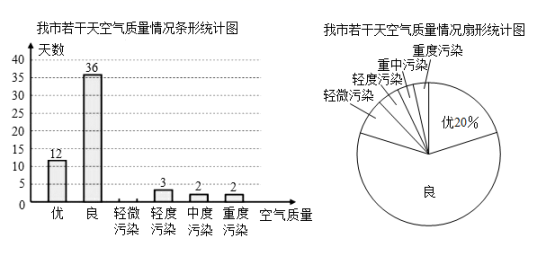
请你根据图中提供的信息,解答下列问题:
(1)、计算被抽取的天数;(2)、请补全条形统计图,并求扇形统计图中表示“优”的扇形的圆心角度数;(3)、请估计该市这一年(365天)达到“优”和“良”的总天数.27. 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.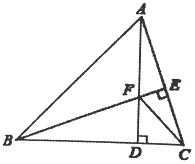 (1)、求证:BF=AC;(2)、若CD=3,求AD的长.28. 如图,AE与BD相交于点C,AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以1cm/s的速度运动,P、Q两点同时出发.当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).
(1)、求证:BF=AC;(2)、若CD=3,求AD的长.28. 如图,AE与BD相交于点C,AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以1cm/s的速度运动,P、Q两点同时出发.当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).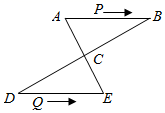 (1)、求证:ABDE.(2)、写出线段AP的长(用含t的式子表示).(3)、连结PQ,当线段PQ经过点C时,求t的值.
(1)、求证:ABDE.(2)、写出线段AP的长(用含t的式子表示).(3)、连结PQ,当线段PQ经过点C时,求t的值.