吉林省长春市宽城区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-10 类型:期末考试
一、单选题
-
1. 若分式的值为0,则x应满足的条件是( )A、x=1 B、x≠1 C、x=-3 D、x≠-32. 下列运算正确的是( )A、 B、 C、 D、3. 一种微粒的半径是0.000041米,0.000041这个数用科学记数法表示为( )A、41×10﹣6 B、4.1×10﹣5 C、0.41×10﹣4 D、4.1×10﹣44. 用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A、有一个内角小于45° B、每一个内角都小于45° C、有一个内角大于等于45° D、每一个内角都大于等于45°5. 用两把完全相同的长方形直尺按如图方式摆放,一把直尺压住射线OB交射线OA于点M,另一把直尺压住射线OA交第一把直尺于点P,作射线OP.若∠BOP=28°,则∠AMP的大小为( )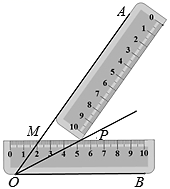 A、46° B、52° C、56° D、62°6. 如图,在和中, ,添加一个条件,不能证明和全等的是( )
A、46° B、52° C、56° D、62°6. 如图,在和中, ,添加一个条件,不能证明和全等的是( ) A、 B、 C、 D、7. 如图,在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法错误的是( )A、
A、 B、 C、 D、7. 如图,在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法错误的是( )A、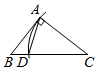 B、
B、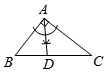 C、
C、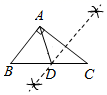 D、
D、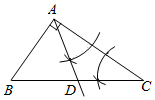 8. 如图,在长方形ABCD中,分别按图中方式放入同样大小的直角三角形纸片.如果按图①方式摆放,刚好放下4个;如果按图②方式摆放,刚好放下3个.若BC=4a,则按图③方式摆放时,剩余部分CF的长为( )
8. 如图,在长方形ABCD中,分别按图中方式放入同样大小的直角三角形纸片.如果按图①方式摆放,刚好放下4个;如果按图②方式摆放,刚好放下3个.若BC=4a,则按图③方式摆放时,剩余部分CF的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
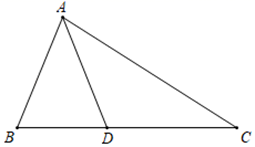
9. 命题“对顶角相等”的逆命题是一个命题(填“真”或“假”).10. 分解因式: .11. 小亮是一位足球爱好者,某次在练习罚点球时,他在10分钟之内罚球20次,共罚进15次,则小亮点球罚进的频率是 .12. 如图,在 中,点D是边BC上的一点.若 , ,则∠C的大小为 .
 13. 现有甲、乙、丙三种不同的正方形或长方形纸片若干张(边长如图).要用这三种纸片无重合无缝隙拼接成一个大正方形,先取甲纸片1张,乙纸片4张,还需取丙纸片张.
13. 现有甲、乙、丙三种不同的正方形或长方形纸片若干张(边长如图).要用这三种纸片无重合无缝隙拼接成一个大正方形,先取甲纸片1张,乙纸片4张,还需取丙纸片张.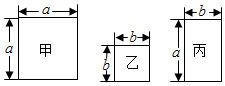 14. 我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭生其中,出水一尺.引葭赴岸,适与岸齐.问水深几何?”(丈、尺是长度单位,1丈=10尺)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇AB,它高出水面1尺(即BC=1尺).如果把这根芦苇拉向水池一边的中点,它的顶端B恰好到达池边的水面D处.问水的深度是多少?则水深DE为尺.
14. 我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭生其中,出水一尺.引葭赴岸,适与岸齐.问水深几何?”(丈、尺是长度单位,1丈=10尺)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇AB,它高出水面1尺(即BC=1尺).如果把这根芦苇拉向水池一边的中点,它的顶端B恰好到达池边的水面D处.问水的深度是多少?则水深DE为尺.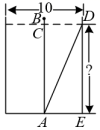
三、解答题
-
15. 计算:16. 计算: .17. 图①、图②均是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,△ABC的顶点均在格点上,只用无刻度的直尺,在给定的网格中,分别按下列要求画图.
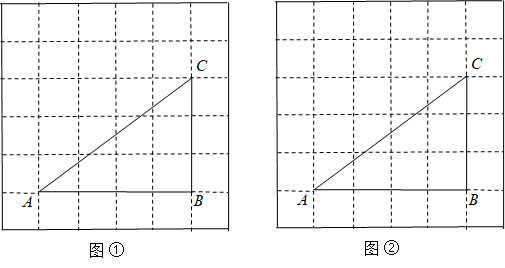
( 1 )在图①中的线段AB上找一点D,连结CD,使∠BCD =∠BDC.
( 2 )在图②中的线段AC上找一点E,连结BE,使∠EAB =∠EBA.
18. 先化简,再求值: , 其中 .19. 为保障新冠病毒疫苗接种需求,某生物科技公司开启“加速”模式,生产效率比原先提高了20%,现在生产240万剂疫苗所用的时间比原先生产220万剂疫苗所用的时间少0.5天,问原先每天生产多少万剂疫苗?20. 如图,在△ABC和△DEB中,AC∥BE,∠C=90°,AB=DE,点D为BC的中点, .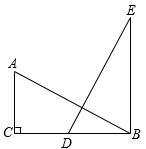 (1)、求证:△ABC≌△DEB.(2)、连结AE,若BC=4,直接写出AE的长.21. 某校在八年级(1)班学生中开展对于“我国国家公祭日(12月13日)”知晓情况的问卷调查.问卷调查的结果分为A、B、C、D四类,其中A类表示“非常了解”;B类表示“比较了解”;C类表示“基本了解”;D类表示“不太了解”;班长将本班同学的调查结果绘制成下列两幅不完整的统计图.请根据图中信息解答下列问题:
(1)、求证:△ABC≌△DEB.(2)、连结AE,若BC=4,直接写出AE的长.21. 某校在八年级(1)班学生中开展对于“我国国家公祭日(12月13日)”知晓情况的问卷调查.问卷调查的结果分为A、B、C、D四类,其中A类表示“非常了解”;B类表示“比较了解”;C类表示“基本了解”;D类表示“不太了解”;班长将本班同学的调查结果绘制成下列两幅不完整的统计图.请根据图中信息解答下列问题: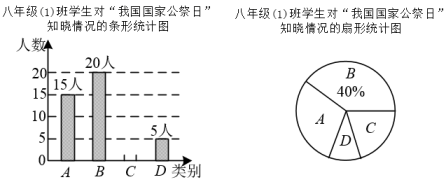 (1)、求该班参与问卷调查的人数.(2)、把条形统计图补充完整.(3)、求C类人数占参与问卷调查人数的百分比.(4)、求扇形统计图中A类所对应扇形圆心角的度数.22.(1)、(教材呈现)图①、图②、图③分别是华东师大版八年级上册数学教材第33页、第34页和第52页的图形,结合图形解决下列问题:
(1)、求该班参与问卷调查的人数.(2)、把条形统计图补充完整.(3)、求C类人数占参与问卷调查人数的百分比.(4)、求扇形统计图中A类所对应扇形圆心角的度数.22.(1)、(教材呈现)图①、图②、图③分别是华东师大版八年级上册数学教材第33页、第34页和第52页的图形,结合图形解决下列问题:
分别写出能够表示图①、图②中图形的面积关系的乘法公式: , .
(2)、图③是用四个长和宽分别为a、b的全等长方形拼成的一个正方形(所拼图形无重叠、无缝隙),写出代数式(a+b)2、(a-b)2、4ab之间的等量关系: .(3)、(结论应用)根据上面(2)中探索的结论,回答下列问题:当m+n=5,mn=4时,求m-n的值.
(4)、当 , B=m-3时,化简(A+B)2-(A-B)2 .23. 定义:如图,点M、N把线段AB分割成AM、MN、NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点. (1)、已知M、N把线段分割成AM、MN、NB,若 , , ,则点M、N是线段AB的勾股分割点吗?请说明理由.(2)、已知M、N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.24. 如图,在等边三角形ABC中,AB=4,点P从点A出发,沿折线A-B-C-A以每秒2个单位长度的速度向终点A运动.点Q从点B出发,沿折线B-C-A以每秒1个单位长度的速度运动.P、Q两点同时出发,点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)、已知M、N把线段分割成AM、MN、NB,若 , , ,则点M、N是线段AB的勾股分割点吗?请说明理由.(2)、已知M、N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.24. 如图,在等边三角形ABC中,AB=4,点P从点A出发,沿折线A-B-C-A以每秒2个单位长度的速度向终点A运动.点Q从点B出发,沿折线B-C-A以每秒1个单位长度的速度运动.P、Q两点同时出发,点P停止时,点Q也随之停止.设点P运动的时间为t秒.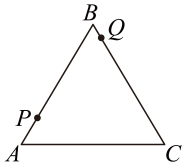 (1)、当P、Q两点重合时,求t的值.(2)、当△BPQ是以PQ为底边的等腰三角形时,求t的值.(3)、当△BPQ是直角三角形时,直接写出t的值.
(1)、当P、Q两点重合时,求t的值.(2)、当△BPQ是以PQ为底边的等腰三角形时,求t的值.(3)、当△BPQ是直角三角形时,直接写出t的值.