吉林省长春市九台区2021-2022学年八年级上学期期末考试数学试题

试卷更新日期：2022-01-10 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数是无理数的是（）

A、 $\sqrt[3]{8}$ B、3.33 C、 $\sqrt{2}$ D、 $\frac{22}{7}$

查看试题解析
2. 下列算式的计算结果为 $a^{6}$ 的是（）

A、 $a^{2} \cdot a^{3}$ B、 $(a^{2})^{3}$ C、 $a^{3} + a^{3}$ D、 $a^{6} \div a$

查看试题解析
3. 以下列长度的三条线段为边，能组成直角三角形的是（）

A、4，5，6 B、8，15，17 C、2，3，4 D、1， $\sqrt{2}$ ， 3

查看试题解析
4. 如图，为了让电线杆垂直于地面，工程人员的操作方法是：从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC，当固定点B，C到杆脚E的距离相等，且B，EC在同一直线上时，电线杆DE就垂直于BC工程人员这种操作方法的依据是（　　）

A、等边对等角 B、等角对等边 C、垂线段最短 D、等腰三角形“三线合一”

查看试题解析
5. 如图，已知△ABC的面积为24，AB＝AC＝8，点D为BC边上一点，过点D分别作DE⊥AB于E，DF⊥AC于F，若DF＝2DE，则DF长为（）

A、4 B、5 C、6 D、8

查看试题解析
6. 如图，已知 $∠ A O B$ ，求作射线 $O C$ ，使 $O C$ 平分 $∠ A O B$ ，那么作法的合理顺序是（）
①作射线 $O C$ ；②在射线 $O A$ 和 $O B$ 上分别截取 $O D$ 、 $O E$ ，使 $O D = O E$ ；③分别以 $D$ 、 $E$ 为圆心，大于 $\frac{1}{2} D E$ 的长为半径在 $∠ A O B$ 内作弧，两弧交于点 $C$ ．

A、①②③ B、②①③ C、②③① D、③①②

查看试题解析
7. 如图，△ABC中，AC＝BC，∠C＝36°，BD平分∠ABC，则图中等腰三角形的个数为（）

A、4 B、3 C、2 D、1

查看试题解析
8. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b．若ab=8，大正方形的面积为25，则小正方形的边长为（）

A、9 B、6 C、4 D、3

查看试题解析

二、填空题

9. 某班50名学生在2018年适应性考试中，数学成绩在100〜110分这个分数段的频率为0.2，则该班在这个分数段的学生为人．

查看试题解析
10. 等腰三角形的两边长分别是5，10，则这个三角形的周长是.

查看试题解析
11. 命题“两直线平行，同位角相等”的逆命题是命题．（填“真”或“假”）

查看试题解析
12. 下列因式分解正确的是（填序号）
① $x^{2} - 2 x = x (x - 2)$ ；② $x^{2} - 2 x + 1 = x (x - 2) + 1$ ；③ $x^{2} - 4 = (x + 4) (x - 4)$ ；④ $4 x^{2} + 4 x + 1 = (2 x + 1)^{2}$

查看试题解析
13. 如图，△ABC中，BC＝10，AB的垂直平分线分别交AB、BC于点D、E，AC的垂直平分线分别交AC、BC于点F、G．则△AEG的周长＝．

查看试题解析
14. 如图， $△ A B C$ 中， $A B = 6$ ， $A C = 4$ ， $D$ 是 $B C$ 的中点， $A D$ 的取值范围为．

查看试题解析

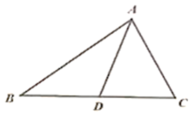
三、解答题

15. 先化简，再求值： ${(x - 3)}^{2} + (x + 3) (x - 3) + 2 x (2 - x)$ ，其中 $x = - \frac{1}{2}$ .

查看试题解析
16. 已知x、y都是实数，且 $y = \sqrt{x - 3} + \sqrt{3 - x} + 4$ ，求 $y^{x}$ 的平方根。

查看试题解析
17. 如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画图形．

(1)、在图1中，画一个等腰三角形（不含直角），使它的面积为8；

(2)、在图2中，画一个直角三角形，使它的三边长都是有理数；

(3)、在图3中，画一个正方形，使它的面积为10．

查看试题解析
18. 配方法是数学中一种重要的思想方法，利用完全平方公式，可将 $x^{2} + 4 x - 3$ 配方成 $(x + m)^{2} + n$ 的形式，即 $x^{2} + 4 x - 3 = x^{2} + 4 x + 2^{2} - 2^{2} - 3 = (x + 2)^{2} - 7$ ．
（解决问题）

(1)、利用配方法将 $x^{2} + 6 x + 2$ 化成 $(x + m)^{2} + n$ 的形式后， $m =$ ， $n =$ ．

(2)、求证：不论 $x$ 、 $y$ 取任何实数，多项式 $x^{2} + y^{2} + 6 x - 2 y + 15$ 的值总为正数．

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B = A C$ ， $D$ 是 $B C$ 的中点， $B E ⊥ A C$ 于 $E$ ．求证： $∠ B A C = 2 ∠ E B C$ ．

查看试题解析
20. 如图，在一条绷紧的绳索一端系着一艘小船．河岸上一男孩拽着绳子另一端向右走，绳端从 $C$ 移动到 $E$ ，同时小船从 $A$ 移动到 $B$ ，且绳长始终保持不变． $A$ 、 $B$ 、 $F$ 三点在一条直线上， $C F ⊥ A F$ ．回答下列问题：

(1)、根据题意可知： $A C$ $B C + C E$ （填“＞”、“＜”、“＝”）．

(2)、若 $C F = 6$ 米， $A F = 8$ 米， $A B = 3$ 米，求小男孩需向右移动的距离（结果保留根号）．

查看试题解析
21. 为弘扬中华传统文化，某校开展“戏剧进课堂”活动．该校随机抽取部分学生，四个类别： $A$ 表示“很喜欢”， $B$ 表示“喜欢”， $C$ 表示“一般”， $D$ 表示“不喜欢”，调查他们对戏剧的喜爱情况，将结果绘制成如图两幅不完整的统计图
根据图中提供的信息，解决下列问题：

(1)、此次共调查了名学生；

(2)、请补全 $D$ 类条形统计图；

(3)、扇形统计图中． $B$ 类所对应的扇形圆心角的大小为度；

(4)、该校共有1560名学生，估计该校表示“很喜欢”的 $A$ 类的学生有多少人？

查看试题解析
22. 如图，长方形纸片 ABCD，AD∥BC，将长方形纸片折叠，使点 D 与点 B 重合，点 C 落在点 C'处，折痕为 EF.

(1)、求证：BE=BF.

(2)、若∠ABE=18°，求∠BFE 的度数.

(3)、若 AB=4，AD=8，求 AE 的长.

查看试题解析

23. （教材呈现）如图是华师版八年级上册数学教材96页的部分内容

已知：如图， $O C$ 是 $∠ A O B$ 的平分线， $P$ 是 $O C$ 上任意一点， $P D ⊥ O A$ ， $P E ⊥ O B$ ，垂足分别为点 $D$ 和点 $E$ ．

求证： $P D = P E$

分析：图中有两个直角三角形 $P D O$ 和 $P E O$ ，只要证明这两个三角形全等便可证得 $P D = P E$ ．

(1)、（问题解决）请根据教材分析，结合图①写出证明

P D = P E

的过程．

(2)、（类比探究）

如图②， $O C$ 是 $∠ A O B$ 的平分线， $P$ 是 $O C$ 上任意一点，点 $M$ ， $N$ 分别在 $O B$ 和 $O A$ 上，连接 $P M$ 和 $P N$ ，若 $∠ P M O + ∠ P N O = 180 °$ ，求证： $P M = P N$ ；

(3)、如图③，

△ A B C

的周长是12，

B O

、

C O

分别平分

∠ A B C

和

∠ A C B

，

O D ⊥ B C

于点

D

，若

O D = 3

，则

△ A B C

的面积为．

查看试题解析

24. 如图，在长方形 $A B C D$ 中， $A B = 4$ ， $B C = 6$ ．延长 $B C$ 到点 $E$ ，使 $C E = 3$ ，连接 $D E$ ．动点 $P$ 从点 $B$ 出发，沿着 $B E$ 以每秒1个单位的速度向终点 $E$ 运动，点 $P$ 运动的时间为 $t$ 秒．

(1)、 $D E$ 的长为；

(2)、连接 $A P$ ，求当 $t$ 为何值时， $△ A B P ≅ △ D C E$ ；

(3)、连接 $D P$ ，求当 $t$ 为何值时， $△ P D E$ 是直角三角形；

(4)、直接写出当 $t$ 为何值时， $△ P D E$ 是等腰三角形．

查看试题解析